一种时间序列数据的动态k-means 聚类算法∗

冀敏杰 肖利雪

（西安邮电大学计算机学院 西安 710121）

1 引言

时间序列是指数据集随着时间变化而变化的数据集，在时间轴上形成连续的序列，它表明了数据内部状态随时间变化的规律。如今，时间序列［1～2］越来越广泛应用与气象［3］、医疗［4］、金融［5］和网络安全［6］等各个重要领域。聚类对于时间序列的分析作为主要研究方法，在现如今的学术领域中备受关注［7～9］。在数据挖掘领域中，聚类分析既可以作为数据挖掘过程中的一个环节，又可以作为获取数据分布情况的工具。

k-means 算法是聚类算法中一种典型的算法，最早由MacQueen［10］提出，具有运算简便，时间复杂度低等优点。k-means 算法的缺点也随着人们的研究而暴露出来，主要包括三点：一是K 值需要预先给定；二是k-means 算法对初始选取的聚类中心点很敏感，不同的中心点聚类结果有很大的不同［11］。三是对于时间序列上的聚类仅仅是多次的静态聚类，没有利用时间序列之间的关联性进行动态聚类。针对这些问题，国内外学者纷纷提出众多的解决方法：Rodriguez A等［12］提出的类簇中心都处在局部密度比较大的位置，运用此思想可以确定最佳初始聚类中心及数据集的最佳类簇数目。贾瑞玉［13］等在这个思想的基础上，运用残差分析的方法，选取残差绝对值大于阈值的异常点作为聚类中心。Lei Gu［14］，M.S.Premkumar［15］和C.Lasheng［16］等采用不同的数学方法确定初始聚类中心。Agrawal等［17］首次提出使用离散傅里叶变换将时间序列的时间域转换为频率域的特征表示方法。文献［18］利用Haar 小波变换表示时间序列数据，采用k-Means 算法和欧氏距离对新特征空间中的数据进行聚类。刘琴等［19］结合滑动窗口及类k-means聚类算法提出了一种基于滑窗不等长时间序列的短时间序列距离的聚类算法，能够解决不等长时间序列聚类的问题，但最佳聚类个数难以确定。谢福鼎等［20］通过等长处理后基于欧氏距离及模糊C 均值聚类算法实现时间序列聚类。上述时间序列聚类算法，均是将长度为n 的时间序列看做n 维空间的一个点，利用处理静态数据的方法聚类时间序列。但是时间序列具有随时间改变的动态性能，相邻时间序列之间具有关联性，静态聚类不能反映时间序列变化的特性。

针对以上问题，本文提出DKCA/TSD 算法。该算法通过时间序列数据之间的关联性，把前一时刻最佳质心应用于后一时刻变化的数据集中，让相邻的时间序列关联起来进行聚类。有效地解决了初始时刻类中心选取困难以及利用时间序列之间的关联性进行动态聚类。不仅在每个时间片上聚类结果更加准确，而且每个时间片上聚类的时间效率更好。

2 k-means算法介绍

2.1 相关定义

其中nj是类Cj中数据对象个数。

2.2 k-means算法

k-means 算法是一种基于样本间相似性度量的间接聚类方法，也被称为K均值算法。算法的主要思想是通过迭代的过程把数据集划分为不同的类别，使得评价聚类性能的准则函数达到最优。算法描述如下：

输入：簇的个数K与数据集合ξ。

输出：K个簇，每个数据所属类别标签。

1）随机选取k个点作为初始聚类别的中心。

2）将数据集中的数据分配到距离最近中心点的类中。

3）使用每个簇中的样本数据均值作为新的聚类中心。

4）重复步骤2）与3）直至算法收敛。

5）结束，得到K个结果簇。

3 时间序列数据及聚类过程分析

3.1 时间序列数据关联性分析

不失一般性，一个时间片上的聚类可以描述：数据集ξ由n 个点组成，x1，x2，…，xn。每个点可用d维表示为xi=（xi1，xi2，…，xid）。给定数据集ξ，聚类算法试图找到一组簇类集合C=｛C1，C2，…，Ck｝使得簇间结构尽可能不同，而簇内结构尽可能相似。其中每个簇的质心点由CEj表示，j=1，2，…，k。与之不同的是，一系列时间片的连续的多个聚类过程，其中两个相邻时刻的连续聚类过程可表示为：ti时刻集合中有ni个元素且构成mi个类。而在时间相邻的ti+1时刻，集合中元素变为ni+1且构成mi+1个类。

假 设 在ti时 刻 中 ，有ni个 元 素 的 集 合 ξi=｛x1，x2，…，xni｝。在ti+1时刻中，有ni+1个元素的集合ξi+1=｛x1，x2，…，xni+1｝。基于ti时刻集合的状态，元素经过元素消失、元素增加、元素位移或者元素不变的情况，形成ti+1时刻集合总元素为ni+1的新聚类的过程，两个连续时刻间ξi与ξi+1中元素的变化大体有以下几种情况：1）元素消失；2）元素新增；3）元素位移；4）元素不变，以下是上述几种元素状态的定义。

定义3 元素消失。ti时刻元素xi∈ξi，ti+1时刻元素xi∉ ξi+1。

定义4 元素新增。ti时刻元素xi∈ ξi，在ti+1时刻元素 ∃xi∉ξi。

定义5 元素位移。ti时刻元素xi∈ ξi，在ti+1时刻元素xi+1∈ ξi+1，∃xi≠ξi+1。

定义6 元素不变。ti时刻元素xi∈ ξi，在ti+1时刻元素xi+1∈ ξi+1，∀xi=ξi+1。

元素的变化导致集合结构发生变化，而相应概率则决定了集合变化趋势。假设ti+1时刻相对ti时刻有w1个元素不变的概率为p1，w2个元素消失的概率为p2，w3个元素新增的概率为p3，w4个元素位移的概率为p4，那么这种情况下从ti时刻变化到ti+1时刻的概率为

为了便于分析，上述四种情况可分为元素发生变化和元素不发生变化两种，假设元素位移、消失、增加的元素变化概率为p，那么元素不变的概率为1-p，则集合ξi变化为ξi+1的概率α为

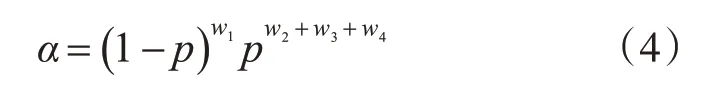
由于ti+1时刻元素数量变为ni+1，而ni+1=w1+w2+w3+w4，则式（2）可写为

显然，ti+1时刻的状态和w1的大小有直接关系。对式（3）求关于w1偏导数有：

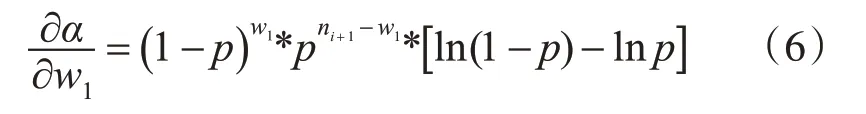
式（4）为0 时，p=0.5 是一个极值点。当p＜0.5时，函数递增，当p＞0.5 时，函数递减。由此可知，当p＜0.5 时且w1越大，形成ti+1时刻情况概率α越大。即当p＜0.5 时，ti+1时刻大多数元素不变时概率最高。

结论1：当p＜0.5 时且w1越大时，ti+1时刻的集合类结构很大程度不会被破坏。也就是说，p＜0.5 时且w1越大时，ti+1时刻类别数目发生改变的概率很小。

3.2 k-means聚类算法在动态聚类过程的案例分析

本节对时间序列上的两个相邻时刻聚类过程分析，采用k-means 算法与DKCA/TSD 算法进行对比分析。如图1（a）是二维平面上ti时刻数据集合ξi=｛1，1；1，2；1.6，1.45；2，1；2，2；2.5，1.55｝，图1（b）是二维平面上ti+1时刻数据集合ξi+1=｛1，1；1，2；1.6，1.45；2，1；2，2｝，显然图1（a）和（b）是时间序列数据相互关联的数据集，即元素F在ti+1时刻消失。为了分析时间序列上的动态聚类的过程，元素新增和元素位移与元素消失的情况类似，故本节只给出元素消失的例子。

对于时间序列上动态聚类，采用k-means 算法对元素消失的情况进行分析，给出ti时刻和ti+1时刻采用k-means 聚类的结果分别如图2（a）和（b）所示。

图2 中不同形状表示不同的类，×表示类的质心。由图2 中（a）可知，当元素F 消失后，采用传统的k-means 算法对变化后的数据进行聚类时，需要调用k-means 算法重新对变化后的数据进行聚类，即重新选取初始质心，重新进行一次k-means 全局聚类。此方法对于每一个时间片相当重新调用了一次k-means 算法，没有达到时间序列数据动态聚类的效果。

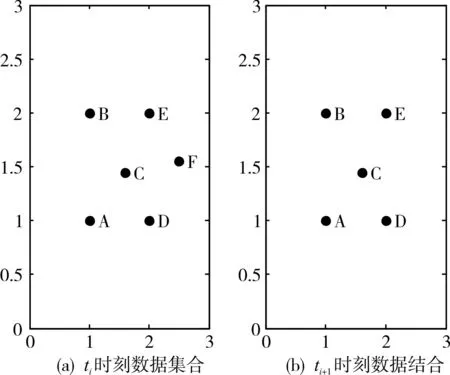
图1 ti时刻和ti+1时刻数据集

针对以上问题，本文提出DKCA/TSD 算法，ti+1时刻的聚类在ti时刻聚类的基础上，继承ti时刻最优的质心点进行聚类，而不用重新聚类中的随机选取质心。由于结论1 可知，变化元素更大概率不会影响原有类结构的破坏，即原有的质心更趋向最优质心，在进行动态聚类的时候更能保证全局最优解以及减少数据的迭代次数，从而减少时间开销。

4 DKCA/TSD算法

从图1（a）到图1（b）的变化过程可知，在ti+1时刻元素F 消失，而图2（b）是采用k-means 聚类的结果，在基于图2（a）的质心上，采用DKCA/TSD 算法的结果如图3所示。

采用DKCA/TSD 算法的计算过程为，当元素F消失后，类2 的质心会向左偏移，由于质心发生了位移，所以需要对剩余的全部元素重新判断属于哪个类。在重新判断的过程中由于元素C 距离类2的质心比较近，故元素C归属于类2，然后重新计算类1 和类2 新的质心如图3 所示，这样就形成了ti+1时刻的聚类，此情况达到最优解的迭代次数仅仅是2 次，而传统k-means 算法在此数据达到最优解迭代次数是4 次。并且，在发生元素变化时，可以挖掘出质心变化过程，上述过程质心的变化过程依次向左移动。

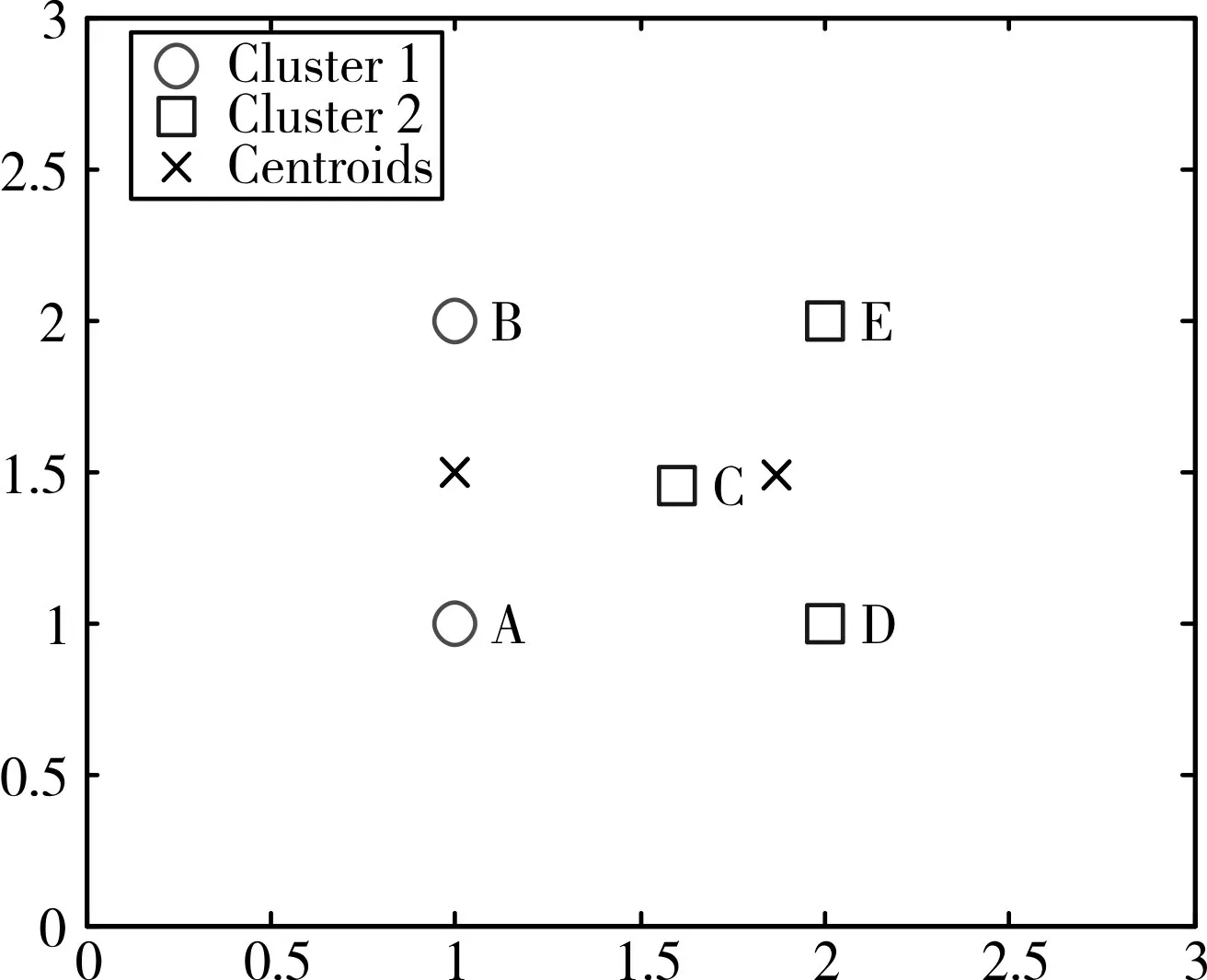
图3 ti+1时刻采用DKCA/TSD算法结果

基于上述分析，给出DKCA/TSD 算法思想和具体步骤。

基本思想：在ti时刻采用k-means 聚类形成最初的聚类，以后的每个时刻基于前一时刻聚类的结果进行时间序列的动态聚类。因为相邻时刻的数据集具有关联性，并且前一时刻聚类结果的质心是最佳质心，变化数据较少的情况下质心移动较小，这样在ti+1时刻的聚类就会减少迭代次数，从而达到更快的达到全局最优解，节省了大量的时间。

DKCA/TSD算法步骤：

输入：ti时刻聚类结果的质心，ti+1时刻数据集

输出：ti+1时刻数据聚类结果以及聚类结果质心

1）记录ti时刻聚类的质心位置。

2）用ti时刻聚类的质心作为ti+1时刻类别中心。

3）将数据集中的数据分配到距离最近中心点的类中。

4）使用每个簇中的样本数据均值作为新的聚类中心。

5）重复步骤3）、4）直到质心不在变化。

5 实验

为了分析传统k-means 算法和DKCA/TSD 算法的性能，本文进行了真实数据和标准数据库SEQUO IA 2000测试。实验采用三个真实数据集Iris、Seeds、Wine，标准数据库SEQUO IA 2000 和人工数据来进行测试。真实数据集Iris数据集包含3 个类和150 个实例，三个类分别为Setosa，Versicolor 和Virginica，每个实例由三个属性表示：萼片长度、萼片宽度、花瓣长度和花瓣宽度；Seeds数据集是由波兰科学院农业物理研究所创建的，数据集代表了三种不同类型的小麦。包含3 个类和210 个实例；Wines 数据集是对意大利同一地区生长但来自三种不同品种的葡萄酒进行化学分析的结果，包括3个类和178 个实例，每个实例有13 种属性。表1 为真实数据集信息说明。

表1 真实数据集信息

5.1 评价指标

本节采用准确率（ACC）、簇内误差平方和（SSE）、迭代次数（N）、运行时间T（单位ms），四个评价指标对所提算法进行了有效性评价。ACC 表示聚类正确的比例，SSE 表示每个数据到质心点的距离和，N 表示聚类算法达到最优时迭代的次数，T表示算法完成聚类所需时间。ACC的值越大，聚类结果越接近于数据集的真实类划分，聚类效果越好。SSE 的值越小，表示簇结构越紧凑，聚类效果越好。N 和T 的值越小，表示算法迭代次数小，运行时间快，聚类的效率越好。

5.2 算法性能比较

本文选择经典的k-means 和本文提出的DKCA/TSD 算法进行比较。为了验证DKCA/TSD 算法的有效性，本文对真实数据集和标准数据集进行规范处理得到时间轴上的数据集。处理过程为每次在数据集范围内随机替换数据集中的5 个数据，一共进行3 次这样的操作，形成时间片上连续的3 个数据集。由于k-means 有初始类中心选择敏感问题，文中采用50次k-means算法结果的平均值作为评价指标。数据集Iris，Seeds 和Wine 在这四种评价指标以及3个时间片上的实验结果分别如表2所示。

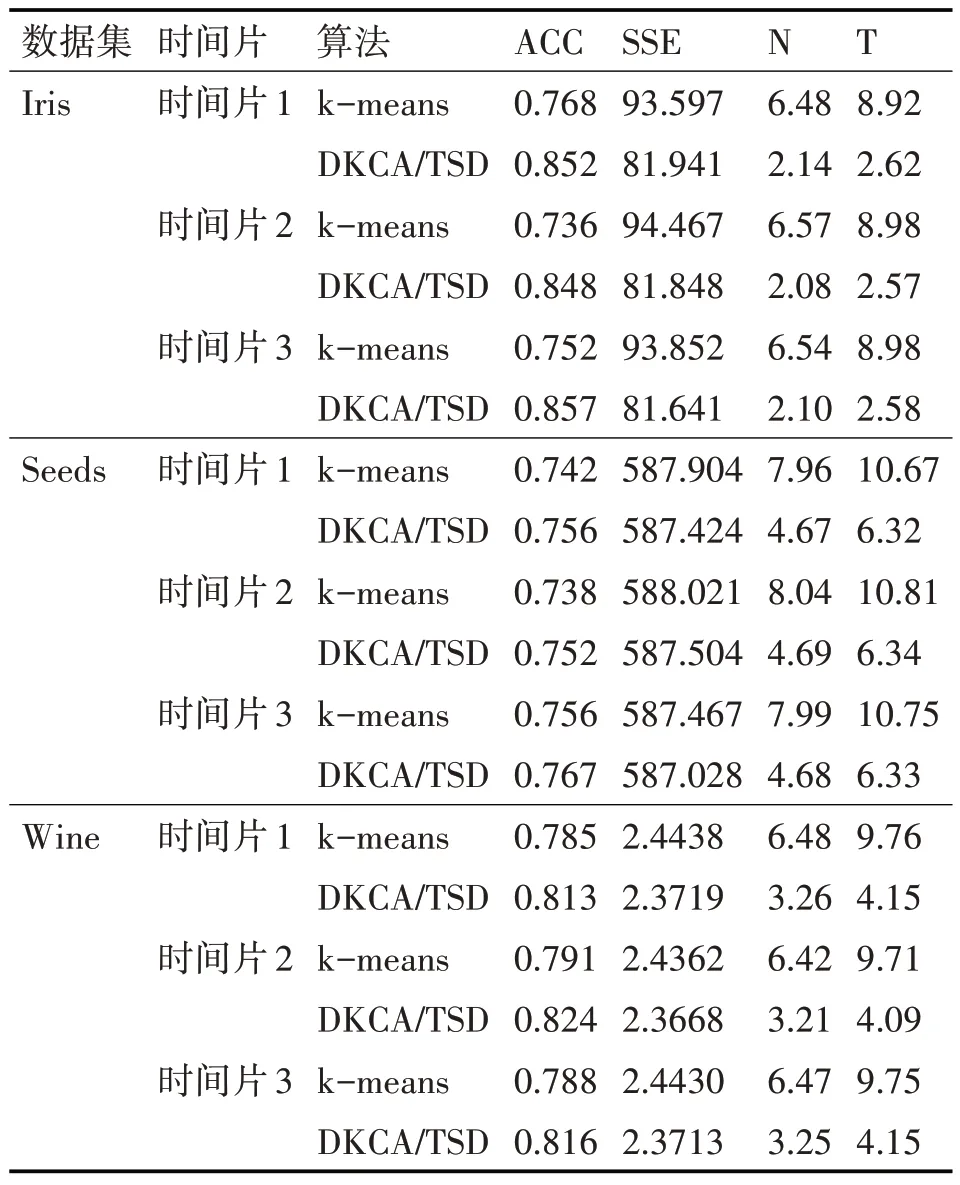
表2 k-means和DKCA/TSD算法在数据集Iris，Seeds和Wine测试结果

由表2 可知，在三个真实数据集中，DKCA/TSD 算法的ACC 指标都比k-means 算法高。尤其在Iris 数据集上，最少提高了8.4%，说明采用DKCA/TSD 算法聚类正确比例高。DKCA/TSD 算法的SSE 指标都比k-means 算法低，尤其在Iris 数据集上，最少减少了2.211，说明DKCA/TSD算法聚类结果更加紧凑，聚类效果更好。再者观察可以发现，DKCA/TSD 算法的N 指标和T 指标都比k-means 要小，平均减少k-means的一半，说明采用DKCA/TSD算法每次迭代的次数更小，运算时间更快。

综上述分析可知，DKCA/TSD 算法相较于k-means 算法，不仅聚类结果更优，而且每次聚类时间效率有所提升。

为进一步DKCA/TSD 算法相对DBSCAN 算法的时间效率有所提升，实验采用SEQUO IA 2000 数据库，处理过程为每次在数据集范围内随机替换数据集种的5 个数据，一共进行3 次这样的操作形成时间片上连续的3 个数据集。数据集采用的数据个 数 分 别 是1000，2000，4000，8000，10000，15000。实验采用指标T 来统计DBSCAN 和DKCA/TSD 算法的时间效率，T 是SEQUO IA 2000 数据集在3个时间片上的平均值。图4是实验结果。

图4 横坐标作为数据库中数据总数，纵坐标为算法执行时间，单位ms。由图4 可知，采用时间序列上的动态k-means 聚类算法的时间效率明显优于传统k-means 算法，尤其在数据集大于4000 时，时间效率差异更加明显。

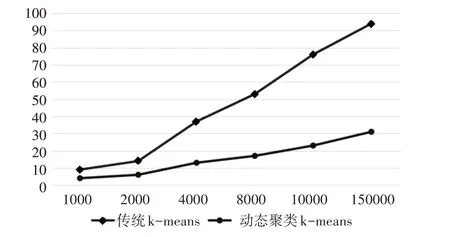
图4 SEQUO IA 2000数据测试的时间结果

6 结语

k-means 算法是一种应用广泛的聚类算法，在历史中取得了很多研究成果。但是对于k-means自身存在的缺点，尤其是在时间序列数据中不能进行动态聚类的缺点。本文提出的算法利用时间序列数据之间的关联性解决了这一难题。本文提出的算法对时间序列数据上聚类的时间效率和聚类结果有很大提升，但对于每个元素在时间序列数据上的动态变化没有体现出来，不具有通用性。那么是否可以借鉴前人研究成果，提出一种新的方法适用于挖掘出时间序列中更具体的簇结构的内部变化，这样的问题值得我们深思，也是作者下一步研究的方向。