一种基于样本学习复杂度的不平衡数据过采样方法∗

许 皓 孙廷凯

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

不平衡数据是指某个类别的样本数远大于其它类别，通常称样本少的类别为少数类（正类），样本数多的类为多数类（负类）［1］。不平衡数据广泛存在于我们的日常生活中，例如，医学诊断［15］，文本分类［16］等。如何识别我们感兴趣的少数类是一个具有挑战性的问题。在设计分类器时，我们必须要考虑到数据的不平衡问题，否则，以最大化分类准确率为目标的机器学习算法会倾向于将测试样本预测为多数类，而忽视少数类的识别率［1］。例如，在临床医学诊断时，普通的机器学习算法倾向于将所有人（包括多数类即健康人和少数类即待确诊的患者）都归类为健康人，这固然得到很高的总体识别率，但对于识别患者却毫无意义。

重采样技术是一种有效用于不平衡数据的方法，它通过增加少数类样本（即过采样）或减少多数类样本（即欠采样），来缓解训练集中类之间的不平衡。欠采样可能会删除某些对分类重要的样本，从而丢失一些有用的信息。而过采样会导致过拟合问题，并可能带来噪声样本。文献［6～8］通过实验，验证了重采样可以提高不平衡数据的分类性能。比如，He 等提出了ADASYN 算法［5］，这是一种基于样本学习复杂度的合成过采样方法。根据该方法的思想，每个少数类样本称为主样本；而将K 近邻中的多数类样本数称为主样本的学习复杂度。ADASYN算法根据学习复杂度的大小，为少数类主样本赋予选择权重，使分类器关注那些学习困难的样本，提升了分类性能。但该方法也存在离散值的复杂度问题，不能充分地表现主样本在学习复杂度方面的差异。

在本文中，我们设计了一种新的基于样本学习复杂度的过采样方法LDSMOTE，用于不平衡数据的分类。与ADASYN 方法不同的是LDSMOTE 方法的样本复杂度计算综合利用了主样本在少数类空间和多数类空间的局部分布，它是一个连续的值，更能表现少数类主样本的学习复杂度。

2 相关工作

针对不平衡数据的分类问题，研究人员提出了许多有效的方法，主要分为数据层的方法和算法层的方法［1］。前者通过调整数据的分布，来缓解训练集中类的不平衡程度。后者通过设计新的分类器，强调学习过程中的少数类，来提高少数类的识别率。算法层的方法包括代价敏感学习、单类分类、集成学习以及基于核的分类等［1］。在本文中，我们主要研究数据层的方法。

数据层的方法一般使用重采样方法调整数据分布以缓解不平衡问题。随机过采样ROS 随机复制若干个少数类样本，强调了原始样本，易产生过拟合问题。随机欠采样RUS 随机删除若干个多数类样本，可能丢弃某些对分类有用的样本，降低分类的性能。由Chawla 等提出的SMOTE 算法［3］是一种合成少数类过采样方法，它随机选择一个少数类样本作为一个主样本，从它的K近邻少数类样本中随机选择一个，将两者的凸组合作为合成样本。它不是简单地复制少数类，减轻了过拟合的影响。但是，该方法对噪声样本敏感，当主样本是一个噪声样本时，新合成的样本有可能也是一个噪声样本。基于这个事实，Han 等提出了一种利用边界位置信息的SMOTE 改进算法，称为Borderline-SMOTE［4］，它将少数类样本分为三类：安全样本、边界样本和噪声样本，并在边界样本上使用SMOTE 算法合成新样本。Borderline-SMOTE 算法合成的样本位于决策边界附近，对决策边界的产生具有显著的意义，并且减轻了SMOTE 算法中传播噪声的影响。对于少数类存在多个子类的情况，DBSMOTE 方法［9］利用聚类算法DBSCAN 对少数类进行聚类，得到多个子类，接着在每个子类上使用SMOTE 算法合成新样本。文献［10］使用基于密度的OPTICS聚类算法计算每个少数类的核心距离和可达距离，将核心距离与核心距离内的多数类样本数的加权和作为主样本的选择权重，使用SMOTE 自适应地合成样本。

除了单一数据层面的重采样技术，大量方法结合使用了采样和集成学习，如文献［11］中的SMOTEBoost，在AdaBoost 的每一次迭代中，通过SMOTE 合成少数类样本来改变每个样本的分布，使得分类器更加关注少数类，从而提高它的识别率。文献［12］中作者将随机欠采样与集成方法相结 合，提出了EasyEnsemble 和BalanceCascade 方法，解决欠采样丢失数据信息的问题。前者独立地使用T 次欠采样得到T 个平衡训练集，学习得到T个AdaBoost分类器，而对一个待测试样本进行类别预测时，将这T 个AdaBoost分类器的预测值进行集成，得到它的类别；后者顺序使用欠采样得到平衡训练集，每次从原始数据集中删除被正确分类的多数类样本。

在本文中，我们设计了一种新的基于样本学习复杂度的过采样方法LDSMOTE，它选择出最重要并且难以学习的少数类样本，根据样本学习复杂度为它赋予选择权重，然后使用SMOTE 算法合成少数类，加入到训练集中，达到平衡正负样本的目的。

3 本文方法

不同于ADASYN 算法，在LDSMOTE 中，样本的学习复杂度包含两个方面，近邻少数类的平均距离和近邻多数类的个数。对于每个少数类主样本xi，它与K 个近邻少数类的平均距离kMinDisti表示了该样本在少数类样本空间中的稀疏程度。它的值越大，意味着少数类样本之间距离很大，即它在少数类样本空间中分布很稀疏，远离了少数类的中心区域，这类样本难以学习，对它应赋予一个更大的权重；反之，该样本在少数类样本空间中密集，这类样本容易学习，应该赋予一个更小的权重。另一方面，在以它的第K 个少数类近邻样本距离为半径的邻域内，多数类样本数nMaji表示了它的局部多数类密度。随着多数类样本数的增多，它位于多数类与少数类的边界区域或位于多数类的中心区域的可能性越大，它的学习越困难，权重应该越大。同时，对这两项值做归一化操作，分别得到K近邻少数类平均距离的归一化值和局部多数类样本数的归一化值，即：

它的值越大，表示越难学习。α 是一个加权系数，表示少数类平均距离对样本学习复杂度贡献的比例。当α 取值为0 时，它与ADASYN 算法相似，都是将它的近邻多数类样本数作为它的学习复杂度，不同点在于：在ADASYN 算法中，K 近邻包含了多数类和少数类，计算的是其中多数类的样本数，只能取［0，K］之间的整数值，所以学习复杂度至多存在K+1 个不同值，它是一系列离散值，这不能充分地表达样本之间的差异性。而在本方法中，少数类的权值可能有大于K+1种不同的取值情况，并且在α 不为0 时，也包括了近邻少数类平均距离，所以学习复杂度是一个连续值，它更能够表现少数类样本在学习复杂度方面的多样性。

从以上算法流程中，我们可以看出：少数类样本被选择作为主样本的次数与它在少数类样本空间的分布和在多数类样本空间的分布都有关，分别对应于它的局部少数类平均距离和局部多数类样本数，实际上，这也对应了它的学习复杂度。图1给出了iris数据（使用第一维和第二维特征，以类别setosa为少数类，其他两类为多数类，o表示少数类，x 表示多数类）中少数类样本的学习复杂度的等高线，可以看出，在边界位置的样本复杂度比中心区域高，所以，在iris 数据集上，本文方法会合成更多对分类器有决策意义的边界样本。

图1 iris数据少数类样本的学习复杂度的等高线

4 实验结果与分析

4.1 数据集

为了验证本文方法的有效性，我们从KEEL 不平衡数据库［13］中选取了一部分的基准数据集，以下的表1 列出了它们的基本信息，包括特征维度、数据集大小、少数类与多数类的样本数以及不平衡比例（多数类：少数类）。

表1 不平衡数据集的基本信息

4.2 评价指标

在不平衡数据的分类问题中，以分类准确率作为指标评价模型的性能是不正确的，本文选用Recall、G-mean和AUC作为模型的评价指标［2］。

4.3 实验设计

本文中所有实验都采用5 重交叉验证的方式，即将数据集划分为5 等份，每次选择其中的4 份作为训练集，剩余1份作为测试集，5次实验结果取平均值作为评价指标。按照以上方式，将数据集打乱后重复进行10 次实验，得到评价指标的均值和方差，作为最终的实验结果。我们对训练集分别使用原始数据ORI、随机上采样ROS、SMOTE、BSMOTE（Borderline-SMOTE）、ADASYN 和LDSMOTE 方法进行处理，使用支持向量机LIBSVM［14］作为分类器，得到分类结果。其中，使用网格搜索策略选择SVM中参数c 和 σ 的值；LDSMOTE 的K 取值都为5，与SMOTE、BSMOTE 和ADASYN 算法中的K 值相同，α 取值为0.9。

4.4 结果与分析

表2、表3 和表4 分别记录了在19 个不平衡数据集上，使用不同重采样方法得出的Recall、G-mean 和AUC 的数值，在每个评价指标中，第一项表示10 次实验结果的均值，第二项表示方差。为了便于观察和比较，我们用粗体标识出每个数据集上的最优结果。

表2 Recall性能对比

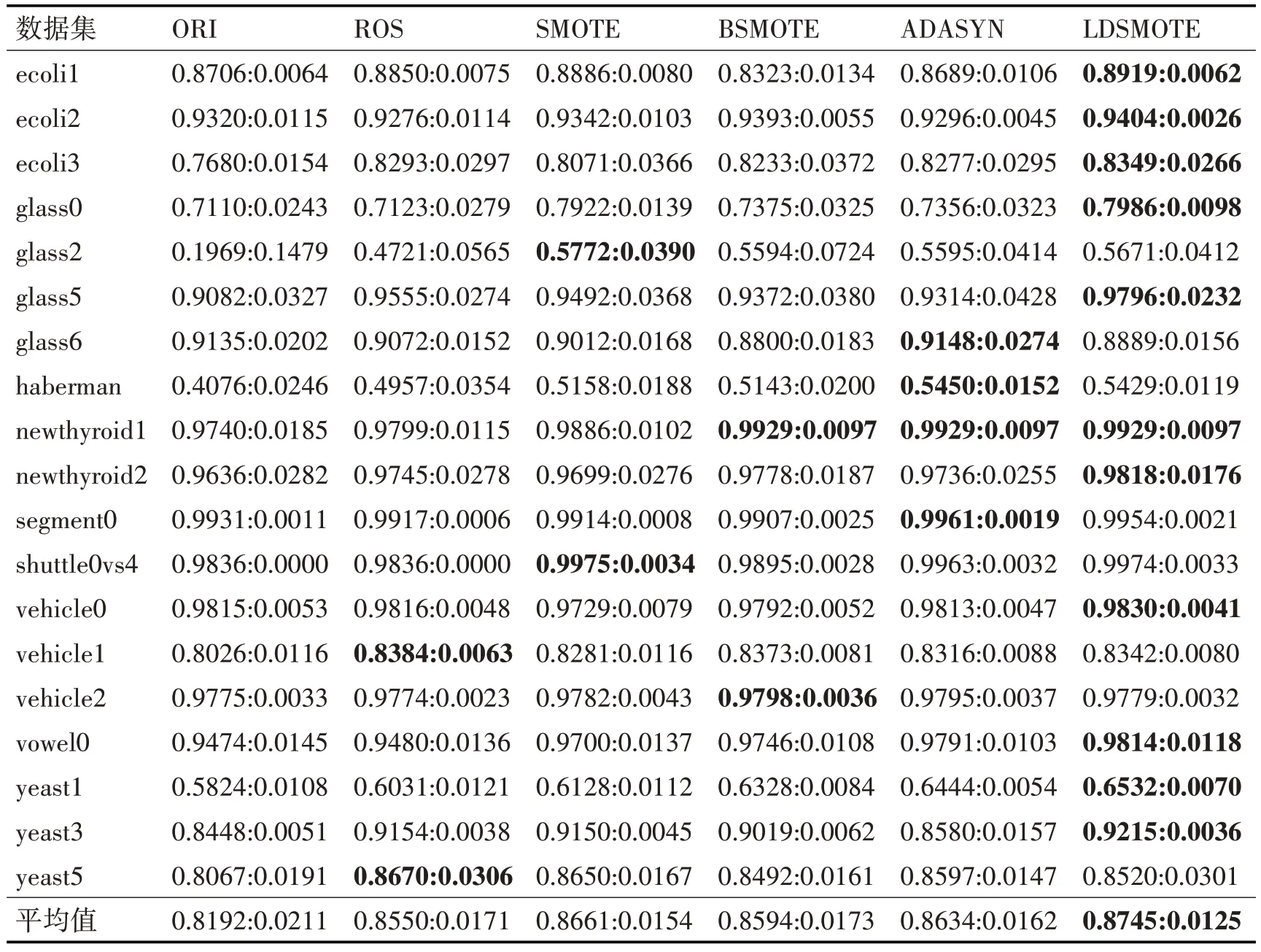
表3 G-mean性能对比

表4 AUC性能对比

从表2 中可以看出，在多数数据集上，使用采样方法平衡样本的分类算法在召回率上都要优于原始的分类算法。实际上，过采样方法通过增加少数类样本调整训练集的数据分布，强调了少数类对学习过程中的贡献度，从而扩张了少数类的决策空间，使得正类样本被正确预测的样本数增多，正类样本被错误预测的样本数减少，所以召回率Recall值比原始的分类结果要好。另一方面，LDSMOTE算法在11个数据集上取得了最优的Recall值，表明了它对少数类的识别率较大。

表3 表示了在19 个数据集上不同重采样方法的G-mean 性能指标。G-mean 的值等于正类准确率与负类准确率的几何平均数，反映了学习算法的综合性能，它的值越大，分类的性能越好。从表3中我们可以看出，在大部分的数据集上，LDSMOTE的G-mean 大于其它方法，表明了它的综合能力较强，在保持多数类高识别率的情况下，能够较大提升少数类的识别率。

从表4 中，我们可以看出LDSMOTE 在超过半数的数据集上取得了最优的AUC值。与SMOTE相比，LDSMOTE 在除了glass6、shuttle0vs4、vehicle2和yeast5 以外的数据集上取得的AUC 值都大于SMOTE；与ADASYN 相比，除了glass6、haberman、segment0、vehicle2 和yeast5 数据 集，LDSMOTE 的AUC 值都大于ADASYN。在vehicle2 数据集上，LDSMOTE 的AUC 结果是过采样方法中较差的，我们认为这可能与噪声样本有关。若存在一个少数类噪声样本，它的K 近邻少数类平均距离很大，并且近邻中多数类特别多，LDSMOTE 会将它的权重设置非常大，在它的邻域使用SMOTE 合成的噪声样本就越多，所以LDSMOTE 在该数据集上的AUC值较低。

5 结语

本文设计了一种新的基于样本学习复杂度的过采样方法LDSMOTE，用于不平衡数据的分类。根据局部少数类平均距离和局部多数类样本数，该方法选择出最重要并且难以学习的少数类样本，对它赋予大的选择权重，在它邻域范围内合成更多的样本。使用支持向量机，对KEEL 不平衡数据库中的19 个数据集进行分类实验，结果表明，在超过半数 的 数 据 集 上 ，LDSMOTE 的Recall、G-mean 和AUC 性 能 优 于SMOTE、Borderline-SMOTE 以 及ADASYN算法。