基于改进的RReliefF 算法的超参数重要性分析∗

梁 鸿 魏 倩 孙运雷

（中国石油大学（华东）计算机与通信工程学院 青岛 266580）

1 引言

在机器学习过程中，算法的性能高度依赖于超参数（Hyperparameters）的选择，超参数选择一直是机器学习过程中至关重要的一步。以贝叶斯优化算法［1～3］为代表的自动化超参数配置方法［4～6］最近在超参数优化方面取得了很大成功，在一些情况下超过了人类专家的性能。

然而，自动化超参数配置方法选择超参数存在一定的约束和限制。这些自动化配置工具只能输出最终的超参数配置结果，却无法评估超参数重要性，也无法解释修改哪些超参数的默认设置可以实现性能的显著性改进。为了向算法开发人员提供不同超参数对性能影响程度的信息，超参数重要性分析方法被提出。

已有的超参数重要性分析方法主要通过随机抽取超参数配置空间中的配置构建模型，根据模型的性能评估超参数重要性。这些方法的局限性在于随机采样的配置仅是超参数配置空间的一部分，不具有整体的代表性，另外构建大量的模型耗费时间。为了解决这些问题，本文首次将特征选择RReliefF 算法用于超参数重要性分析，并对RReliefF 进行改进和融合用于评估超参数及超参数之间的重要性。该算法直接根据每一个超参数对性能的影响程度去估计这个超参数对性能贡献的能力，对单个超参数进行评估之后，使用归一化方法对超参数之间的重要性进行评估，且与既有方法相比具有更高的效率。

2 相关工作

针对自动化超参数配置算法的弊端，科学家们提出了评估机器学习算法超参数重要性的方法。2006 年bartz-beielstein［7］等使用等高线可视化探索交互式参数，这种方法无法处理算法配置场景中分类超参数所构成的离散配置空间。2007 年Nannen［8］等提出了关于参数相关估计的进化算法，该方法对超参数响应面进行平滑性假设，消除了分类超参数的影响，只能处理较少的超参数。

为了解决离散性超参数的问题，Hutter 等使用基于模型的技术研究超参数重要性和超参数相互作用的问题，提出了前向选择算法和functional ANOVA 算法等。前向选择（Forward Selection）算法［9］迭代贪婪的增加超参数，这些超参数在验证集中具有最小均方根误差，以此迭代的建立回归模型。functional ANOVA［10］算法将方差分解应用到随机森林模型中评估超参数重要性。这些算法虽然在处理算法配置空间的高维性和离散性方面表现出色，但需要迭代构造模型，导致时间复杂度增加。

3 超参数重要性评估

自动化超参数配置能够得到机器学习算法的最优超参数组合。但由于其内部过程的抽象性及黑盒性，无法分析超参数重要性程度。现有的超参数重要性评估方法需要迭代建模才能得到超参数重要性权重。为了避免建模造成时间复杂度增加的同时了解算法本身超参数的重要性排序，本文提出一种改进的RReliefF 算法用于超参数重要性评估。

3.1 Relief算法

Relief 算法［11］最初用于特征选择领域。Relief算法的主要思想是根据每一个属性对实例的区分程度去估计这个特征区分临近样本的能力。Relief的流程是：在训练集中随机选取一个实例I ，搜索与实例I 相近的k 个实例Ij，Ij中与实例I 属于相同类别的样本称为H ，相异类别的样本称为M［12］。根据实例I ，以及Ij中的H 、M 的值对属性A 的权重W[A]进行估计，并由式（1）所示的概率差的近似值获得：

如果实例I 和H 具有不同的属性值A，那么属性A 将两个实例与同一类的实例分离，在公式体现为减少权重估计W[A]。如果实例I 和M 具有不同的属性值A，那么属性值A 将两个实例与不同类的实例分离在公式体现为相应增加权重估计W[A]。特征的权值越大，表示该特征的分类能力越强；反之，表示该特征的分类能力越弱［13］。

其中，W[A]中不同实例I1和I2对于属性值A的差异定义为［13］

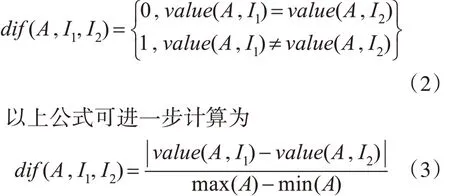
3.2 改进的RReliefF算法

为了对机器学习算法的超参数重要性进行评估，本文提出一种改进的RReliefF 算法用于超参数重要性评估。该算法分为两部分，第一部分首次将特征选择算法——RReliefF［14］算法用于单个超参数重要性评估。第二部分针对RReliefF 算法只能评估单个超参数重要性的弊端，使用改进的归一化公式计算超参数之间的重要性权重。

超参数重要性评估使用的输入数据为机器学习算法的超参数配置和其性能数据。在此类数据集上，性能数据是连续值，不能使用Relief 中提出的最近的同类和不同类样本进行计算。为了解决此类问题，引入了两个相异实例的概率来判断两个实例是否属于同一类，该概率定义可以模拟与预测两个实例的相对距离。

改进的RReliefF 算法用于超参数重要性评估的主要思想是根据每一个超参数对性能的影响程度去估计这个超参数对性能贡献的能力。改进的RReliefF 算法由两部分构成，第一部分是对单个超参数重要性进行评估：在训练集中随机选取一个超参数配置实例I ，选择与实例I 相近的k 个实例Ij，为了判断实例Ij与I 是否属于同一类，引入概率模拟和预测两个实例的相对距离［14］，如式（4）所示。其中θ 表示超参数，PdifA表示相近实例中超参值不同的概率；PdifC表示相近实例中类别不同的概率；PdifC/difA表示在超参值相异的相近实例中类别相异的概率。

重复以上过程k 次可得出W[θ]，根据W[θ]权重大小对单个超参数重要性进行评估。

第二部分针对RReliefF 算法只能评估单个超参数重要性的弊端，使用改进的归一化公式计算超参数之间的重要性权重。该算法使用超参数之间的贡献除以所有超参数贡献的总和来归一化（Normalization）计算超参数之间的重要性。公式定义如（7）所示：

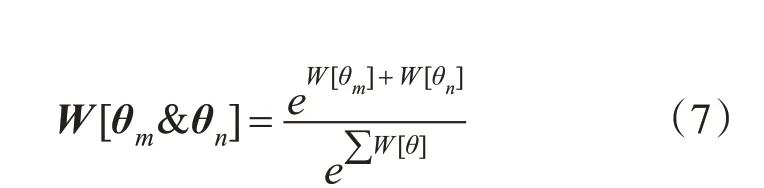
θm和θn表示两个不同的超参数，表示所有超参数重要性权重之和。这个公式是对归一化公式的变形，可以更加稳定地评估超参数之间的交互作用对性能的影响。

改进的RReliefF 算法的整体流程是：首先计算各个超参数对性能的贡献（权重）向量，对向量中的元素进行累加，利用累加值对各个超参数重要性排序，选择重要性较强的t 个显著超参数进入超参候选子集，由此开始迭代过程。在迭代过程中，计算显著超参数之间的重要性权重，最终输出所有超参数及超参数之间的重要性权重。算法流程如算法1所示。

算法1：改进的RReliefF算法

算法中Ndc，NdA[θ]，NdC&dA[θ]分别表示不同预测值的权重向量（第6 行），不同属性的权重向量（第8）行），不同预测值及属性的权重向量（第9）行）。算法14）行计算了每个超参数的重要性权重W[θ]。 Hlist表示最重要的前t 个超参数［15］。

变量d(i,j)（第6），8），9）行）用于衡量两个实例Ri和Ij的距离，基本原理是更接近的实例应该具有更大的影响：

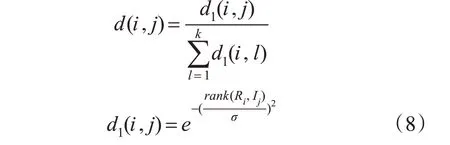
rank(Ri,Ij)是实例Ij与实例Ri距离的排名，σ用于控制距离，由用户自定义而来。由于希望结果可以进行概率解释，将κ 近邻实例中的每个实例的贡献将其除以所有k 个贡献的总和来归一化。使用排名而不是实际距离的原因是实际距离与具体问题有关，而通过使用排名，我们确保最近实例始终对权重具有相同的影响［16］。

改进的RReliefF 算法无需迭代建模即可直接评估不同超参数的重要性，为每个超参数赋予一个权重值的同时，也评估超参数之间是如何影响权重的，以此来确定一系列最重要的算法超参数。重要性权重大的超参数及超参组合表示这些超参数调节的好坏对机器学习算法性能的优劣至关重要，而其他权重不大的超参数则表示即使反复调节此超参数，对机器学习算法性能影响也不大。当计算资源有限时，可以重点调节权重大的超参数，对于权重小的超参数可以在机器学习算法中使用其默认值。当有足够的计算资源时，仍然建议调整所有超参数。该算法能够识别机器学习算法中重要的超参数，其结果可以指导贝叶斯优化算法对超参数的优化，提升算法的性能与效率。

4 实验

超参数重要性评估算法的实验数据是自动化超参数配置算法结束后产生的超参数配置及性能数据，利用这些数据评估机器学习算法超参数及组合的重要性，得到对算法性能影响重大的一系列超参数。本节还将改进的RReliefF 算法与forward selection和functional ANOVA两种超参数重要性评估算法进行对比，分析SVM 和随机森林两种分类器的相对超参数重要性权重以及算法运行的效率。

4.1 实验数据及方法

为了获得改进的RReliefF 算法适用的超参数配置及性能数据，本节使用自动化超参数配置方法中具有代表性的贝叶斯优化算法［17～18］对来自Open-ML100［19］的数据集进行了所有的实验。Open-ML100 是一个基准测试套件，包含来自不同域的100 个数据集，数据集包含500 到1000 个分布均衡的数据点。

对来自OpenML100 的数据集上分析两种分类方法：SVMs［20］和随机森林［21］。对于SVMs，分析其中两种核函数类型：径向基核函数（Radial Basis Function，RBF）和sigmoid 核函数。所有算法使用相同的数据预处理步骤，包括对缺失数据进行插补，对离散型特征使用独热码（One-Hot-Encoding）编码。支持向量机对输入变量的比例敏感，需要对输入变量进行标准化。

数据预处理结束后，对每一种分类方法使用贝叶斯优化算法进行调优。为了保证超参数调优方法不会因为超参数的配置空间而产生任何偏差，本节使用相同的超参数类型及范围。两种算法的超参数类型及范围如表1、2 所示。两种分类器在OpenML100 上经过贝叶斯超参数调优产生超参数配置数据及相应的性能数据，我们利用这些数据进行超参数重要性分析。

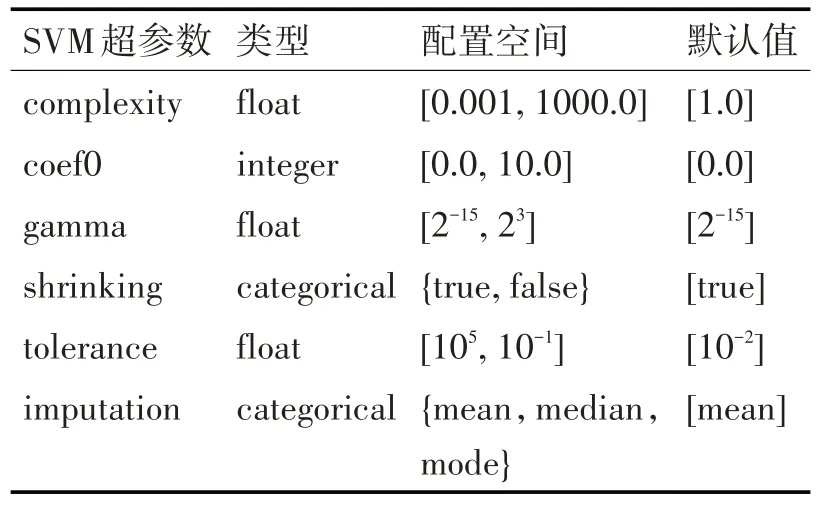
表1 SVM算法中超参数配置空间

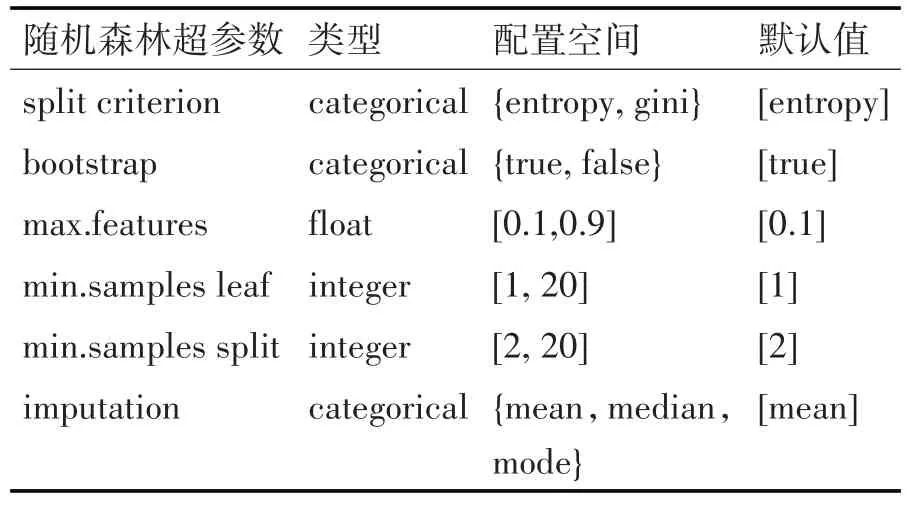
表2 随机森林算法中超参数配置空间

4.2 实验结果

本节分析改进的RReliefF 算法用于确定每个分类器最重要的超参数的实验结果。对每个分类器使用图1、图2、图3 展示超参数及超参数组合的平均超参数重要性，X 轴表示超参数及超参组合名称，Y 轴表示超参数重要性权重。权重越高代表超参数或者组合对性能影响越大，如果不能将其调整到合适的值会使算法精度下降。

对每个分类器使用表3、表4、表5 展示forward selection、functional ANOVA 算法、改进的RReliefF算法对每种分类器的超参数进行评估获得的重要性权重，同时对比了三种算法的运行时间。

1）SVM 结果。图1 和图2 分析了SVMs 的两种核函数，分别为RBF 核函数和sigmoid 核函数。实验结果清晰的展示了两种情况下最重要的超参数均为gamma，次重要的为complexity。表3 和表4 分别对SVM（RBF 核）和SVM（sigmoid 核）使用forword selection 算法、functional ANOVA 算法进行了验证，这两个超参数重要性评估方法对SVMs 的两种核函数进行分析同样得到gamma 是最重要的超参数，complexity次之，且三种算法的超参数重要性排序结果基本一致，改进的RReliefF 算法运行时间更短。

图2 中显示，在使用sigmoid 核时，超参数gamma 与complexity 之间的相互影响比complexity 参数本身对算法的影响更重要。由经验可知，gamma和complexity 是SVM 中重要的超参数。本文则使用广泛的数据集为传统经验提供系统的验证。对于SVM 的准确性而言最不重要的超参数是是否使用收缩启发式算法（shrinking heuristic）。此超参数旨在减少计算资源而不是提高预测性能，根据改进的RReliefF 算法计算超参数对性能影响的标准而言，它的重要性权重符合实际结果。

图1 改进的RReliefF算法评估SVM（RBF核）超参及组合重要性

表3 SVM（RBF核）中超参数重要性权重及不同方法的运行时间

图2 改进的RReliefF算法评估SVM（sigmoid核）超参数及组合重要性

2）随机森林结果。图3 展示了随机森林算法的实验结果，随机森林算法的高性能是由少部分超参数贡献而来的。每个叶子的最小样本数（min.samples leaf）和决定分割的最大特征数（max. features）是最重要的超参数。实验过程中，仅在少数的数据集上，bootstrap 是最重要的超参数。超参数split criterion 仅在数据集“scene”中表现为最重要。同样，本实验结果与表5 展示的forward selection、functional ANOVA 算法对随机森林算法超参数重要性排序结果基本一致，且改进的RReliefF 算法效率更高。

表4 超参数重要性权重及不同方法的运行时间

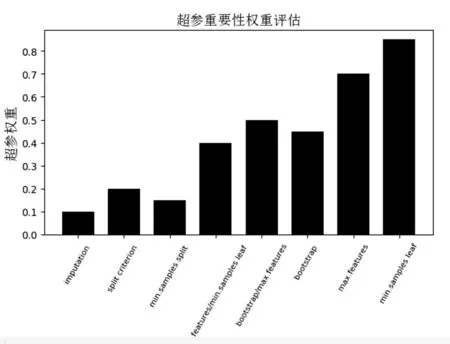
图3 改进的RReliefF算法评估随机森林算法超参数及组合重要性

3）最终结论。对于所有分类器而言，大多数情况下性能的变化取决于一小部分超参数，在许多情况下，相同的超参数在不同的数据集上重要程度相似。对于SVMs 来说，超参数gamma 和complexity是最重要的，对于随机森林而言，每个叶子的最小样本数和决定分割的最大特征数是最重要的。为了验证实验结果，改进的RReliefF 算法与多个超参数重要性评估算法进行对比，所得超参数重要性排序与其他算法所得结果基本一致，并且在很大程度上与流行的观点一致。同时，改进的RReliefF 算法无需建模即可评估超参数重要性，与其他建模评估超参数重要性的方法相比具有更高的效率。

实验结果还表明超参数插补策略（imputation strategy）对于分类器的性能而言关系不大，在人们的经验中，插补策略是重要的，但本实验表明对于插补而言，使用哪种策略进行对结果的影响不大。初步分析这是限制于本实验所使用的几种插补策略差别不大所导致的，进一步证明此结论还需要进行整体研究，增加其他插补策略（例如，基于模型的插补方法，多重插补等）。

本节中提供的分类器超参数重要性结果在计算资源缺乏的时候，可以指导算法研究人员优先调整重要性权重大的超参数。这样可以用较短的时间提升较大的性能，但当有足够的计算资源时，仍然建议调整所有超参数。

5 结语

本文通过改进的RReliefF 算法无需建模即可评估超参数重要性，该算法在数据集上评估分类器上超参数及超参数之间相互作用的重要性，与相关方法比较具有一定的优势。

未来的工作将分析重要性超参数的哪些值是重要的，为用户提供能够获得更优性能的超参数的范围和信息。还会分析更多分类器上的超参数重要性，另外还可以扩展到回归和聚类算法上，为机器学习算法超参调数优领域提供有用的实验支持。此外，还会将算法扩展到深度学习领域，对各种网络模型（例如：CNN、RNN 等模型）进行调优并判断超参数重要性。