大吨位主捆绑机构力-热耦合特性研究

张 薇，顾名坤，容 易，秦旭东，赵 婷

（北京宇航系统工程研究所，北京，100076）

0 引 言

捆绑式运载火箭借助于捆绑结构将助推器连接在芯级周围，能够大幅提高起飞推力，增强火箭运载能力，节约火箭发射成本[1]。有研究表明，固体捆绑式助推器可使得火箭运载能力提高70%左右[2]，对于大型运载火箭，捆绑结构的可靠性是一项关键技术[3]。一种基于球头-球窝配合的捆绑结构普遍应用于捆绑式火箭芯级与助推器的连接，作为传递发动机轴向力的主传力结构，它既能够传递较大载荷，又能适应装配时助推器与芯级的位置与角度偏差。

在飞行过程中，由于高速气流和发动机推力的作用，助推器相对于火箭芯级发生转动，导致捆绑结构中的球头-球窝在传递较大载荷的同时发生相对转动，球头-球窝接触面之间产生相对摩擦[4]。根据工程估算，摩擦面接触压强高达到上千兆帕，摩擦会导致局部温度急速上升，降低材料的强度，从而影响捆绑结构的承载能力。因此，在多项载荷作用下，球头-球窝配合结构的接触摩擦生热对结构强度的影响成为捆绑结构设计的一个关键因素。

1 捆绑结构模型

典型球头-球窝配合捆绑结构，球窝与芯级捆绑连接座相连，球头与助推器捆绑连接座相连。在飞行过程中，球头与球窝允许发生微小的转动，适应助推器与芯级之间的相对变形。在飞行过程中，球头受到助推器的作用，产生3 个方向的推力，通过球头-球窝配合结构传递给芯级连接座，从而推动火箭芯级上升。

2 摩擦生热计算方法

球头-球窝在相对转动过程中的，接触面处存在较大的摩擦力，摩擦力与接触压力和摩擦系数存在着密切关系，因此要分析摩擦生热，首先必须分析接触面上的接触压力。

对于弹性固体接触模式，Hertz 给出了不同形状物体接触时，接触面处的变形和接触区域大小计算方法[5]（Hertz 接触模型如图1 所示）。在集中载荷zF 的作用下，假设球窝的标称半径为R。假设结构材料相同，泊松比为0.3，球头-球窝接触形式的啮合深度δ 可以表示为

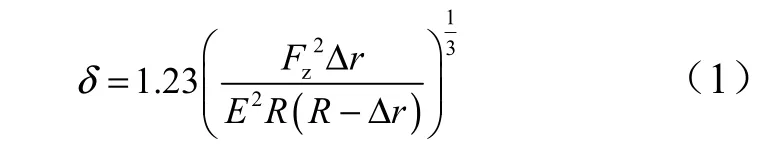
式中 rΔ 为球头与球窝半径之差；E 为材料弹性模量。

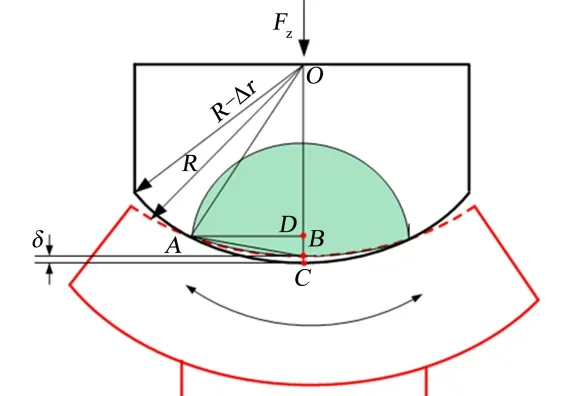
图1 球头-球窝Hertz 接触模型Fig.1 Hertz Contact Model of Ball-head and Ball-pocket

根据Hertz 接触模型，球头-球窝接触区域的横向长度2a 可以表示为

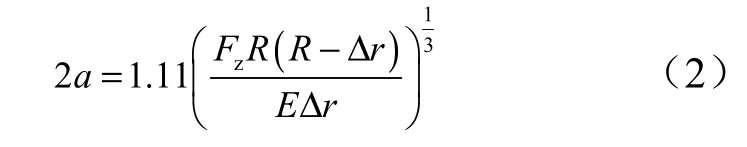
那么球头-球窝在接触面上的平均接触压力就可以表示为

式中 ε 为接触面积修正系数，取0.38。

球头-球窝摩擦接触过程中的转动频率为f，球头发生周期转动的最大转角幅度为θ（弧度制），接触面上的相对运动的平均速度v 可以表示为

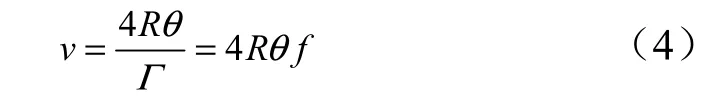
式中 Γ 为转动的周期。

接触面上的摩擦生热速率可以表示为

式中 PW为生热速率；μ 为接触面摩擦系数；S 为摩擦面积，即球头与球窝的接触面积。

如图1 所示，在球头-球窝结构受力变形后，接触区域可以近似等效为以球面弧长为半径的球面，设的弧长为 b，由于变形非常小，所以可以认为b =≈ AB ，根据几何关系可以得到：

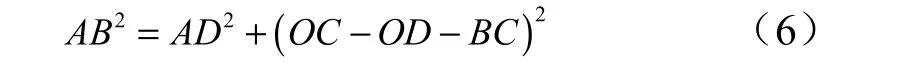
在小变形条件下，计算过程中忽略δ 和 rΔ 的二阶小量，那么可以得到：

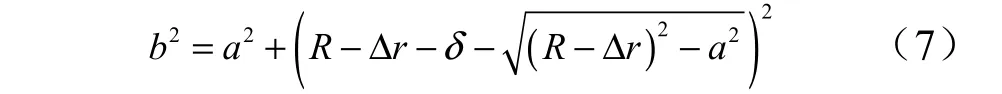
局部摩擦生热面积可以表示为

将式（4）和式（8）代入式（5）中可以得到：

在极短的时间内，假设球窝与球头接触带温度变化率可以表示为

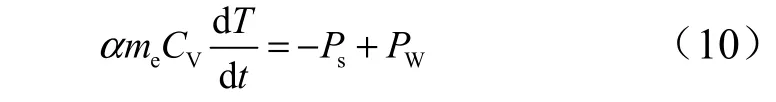
式中 me为球头-球窝接触带吸热的材料等效质量；α为质量修正系数；第2 项为接触带周围散失的热损失；VC 表示材料的比热容。

参考集中参数法[6]，散失的热量与导入热量拟合为

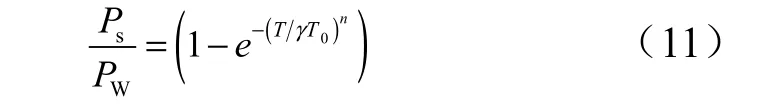
式中T0为参考温度， T0=273 ℃；n=0.2。

球头接触面温升区域可以近似等效为圆锥体，那么其可以表示为

式中 h0为等效圆锥体的高度。

将式（12）带入式（10）中，可以得到：

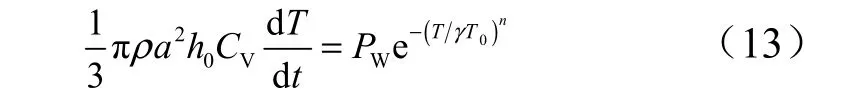
将式（11）和式（12）代入式（13）进一步化简可以得到温升与接触压力的变化关系为

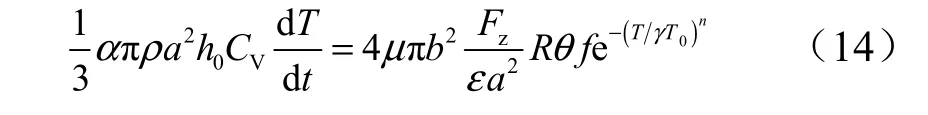
将式（3）和式（9）代入式（13），那么温度的上升速率就可以表示为

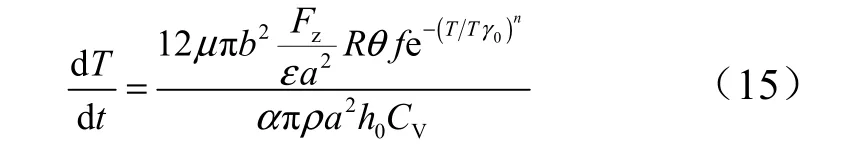
上式反映温度与球头-球窝半径之差的关系，其中包含在计算平均压力的面积修正参数ε、在计算温升变化时用于修正温升区域的等效材料质量的参数α 和用于修正热散失项的参数γ 。

3 有限元分析模型

沉淀硬化不锈钢PH13-8Mo 是一种超高强度的不锈钢，常温下的屈服极限达到了1517 MPa，杨氏模量为200 GPa，泊松比为0.3，其强度和热力学参数随温度的变化如表1 和表2 所示。可以看到当温度超过400 ℃时，材料强度迅速下降。

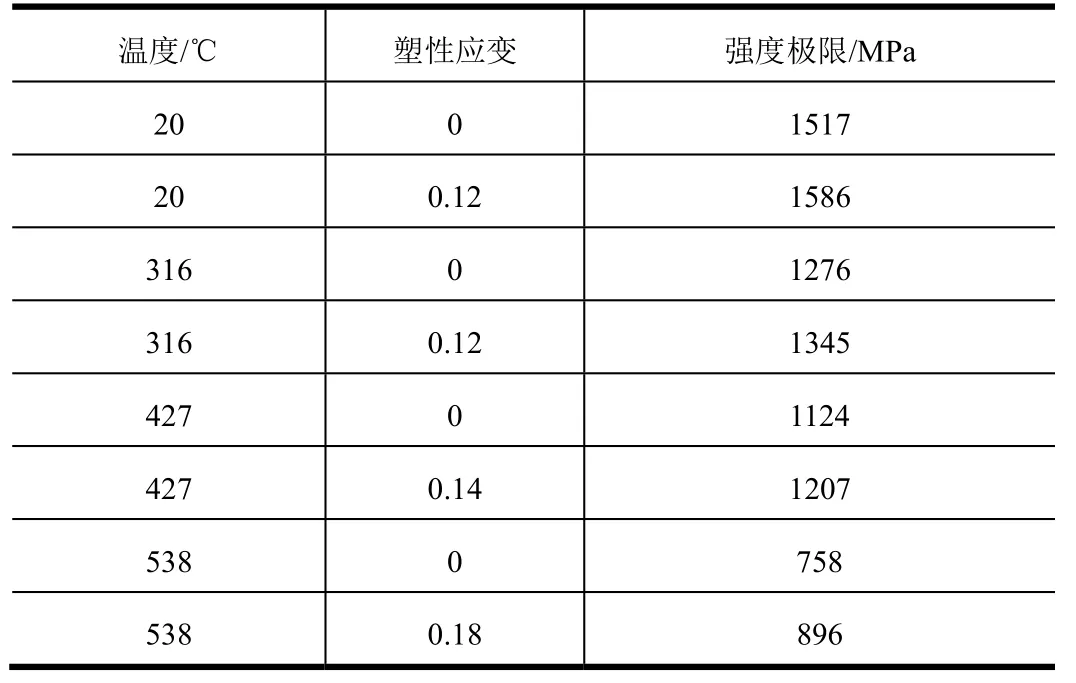
表1 材料力学参数Tab.1 Mechanical Parameters

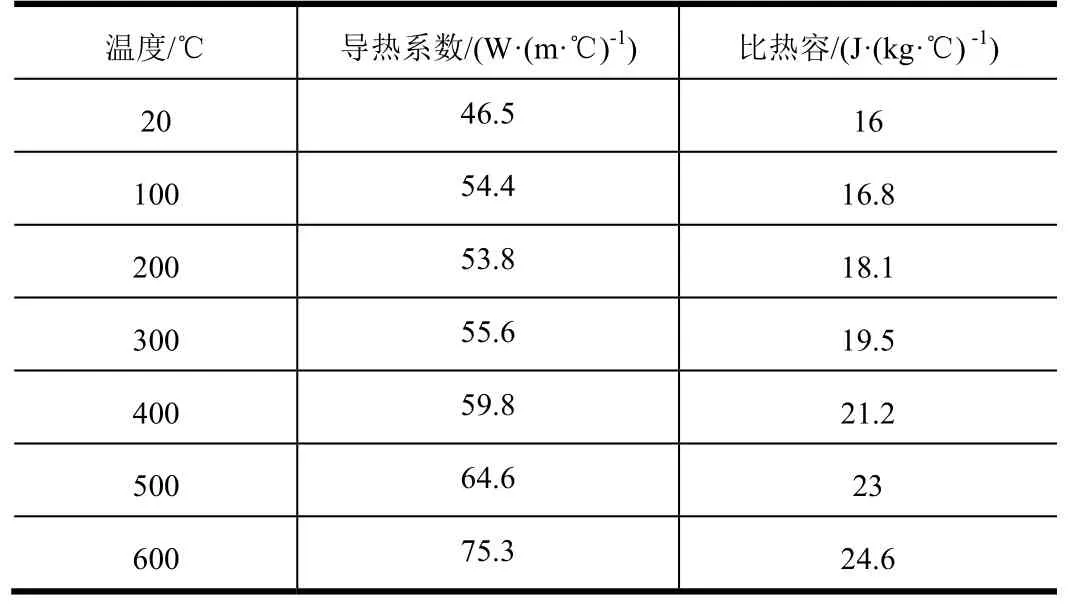
表2 材料热学参数Tab.2 Thermal Parameters

火箭飞行过程中球头-球窝作用时间大约为150 s，3 个作用力随着推进剂燃烧和飞行速度的增大逐渐变化，整体模型采用热力耦合算法，将会消耗大量的计算时间。在不影响分布情况下，将模型简化，基本网格尺寸为5 mm，接触面处进行网格加密，最小基本网格尺寸为2 mm，生热计算过程单元类型为C3D8RT。根据局部生热温度变化，将材料模型等效为随载荷变化的参数，并进行3 项载荷作用下的强度计算。

4 球头-球窝转动生热分析

根据上述描述，首先分析不同球头-球窝半径匹配对摩擦生热的影响。施加载荷Fz，给另一端施加周期转动，转角幅值为2°，频率分别为2 Hz、5 Hz 和8 Hz。当球窝直径保持不变时，球头直径变化会影响到接触面积的大小，导致作用到球窝的压力变化，最终影响到生热速率的改变。分别对球头半径为75 mm、74.9 mm、74.8 mm、74.7 mm、74.6 mm、74.5 mm 与球窝半径为75 mm 模型进行数值分析，分析时间为10 s，加载压力为1 733 266 N。

4.1 球头半径对接触压力的影响

图2 表示接球头-球窝接在集中载荷作用下，球窝表面的接触压力分布云图。根据接触压力分布云图可知，当球窝与球头半径都为75 mm 时，边缘承受较大的接触力，最大接触压力为654 MPa；当球头半径减小0.1 mm 时，最大接触力出现在球窝中心，此时接触压力为956 MPa，随着球头半径减小，球窝与球头的接触面积减小，接触压力增加；当球头半径为74.8 mm时，球窝边缘的接触压力已经变为0 MPa，此时说明球头-球窝已经不再是完全接触。

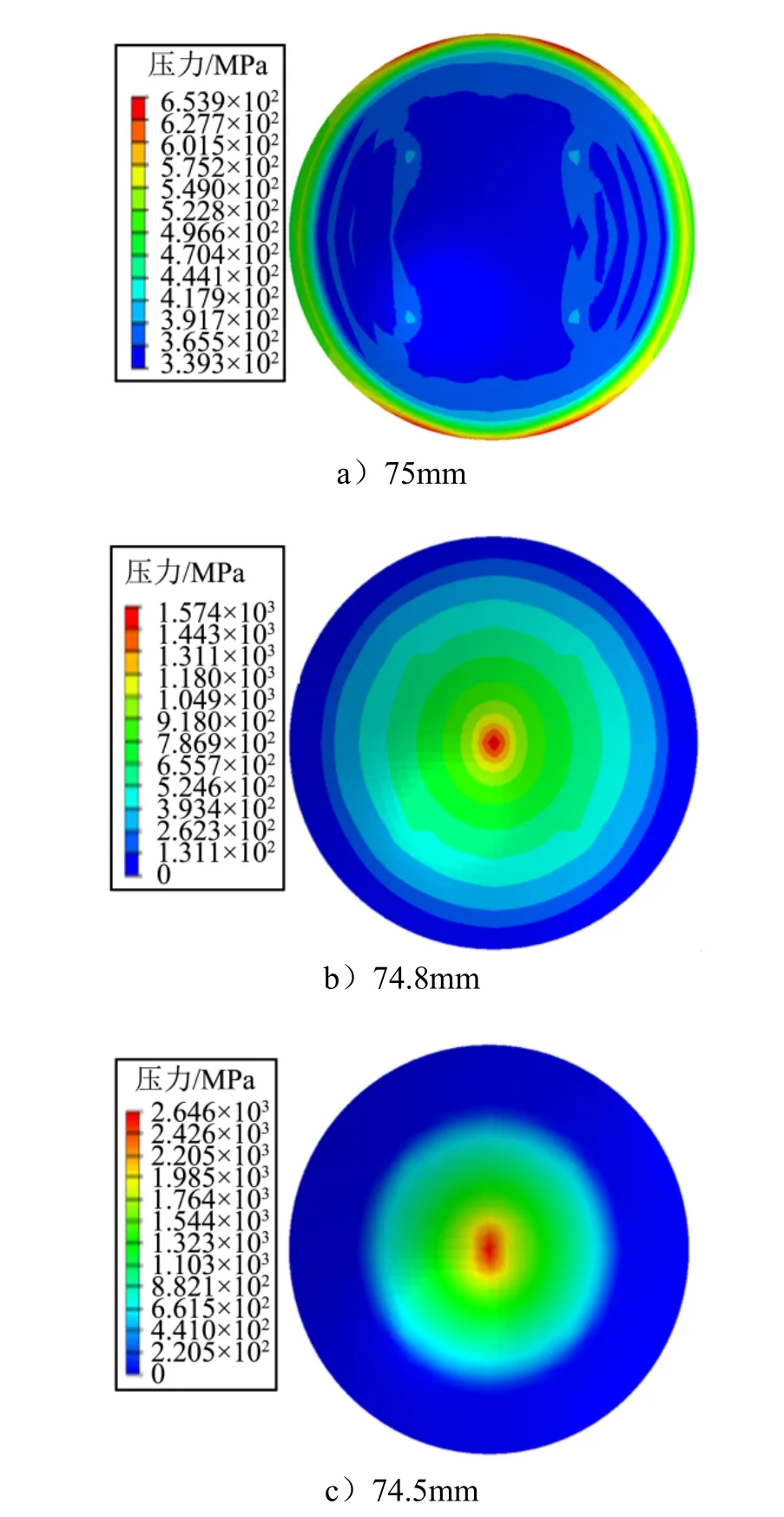
图2 接触压力分布云图Fig.3 Contact Pressure Distribution Nephogram

提取球窝中心的接触压力绘制接触压力随半径的变化关系如图3 所示。由图3 可以看出，球窝接触压力随着球头半径的减小呈线性减小，且通过式（3）计算的接触压力能够很好与仿真值吻合，标定面积修正系数为0.38。

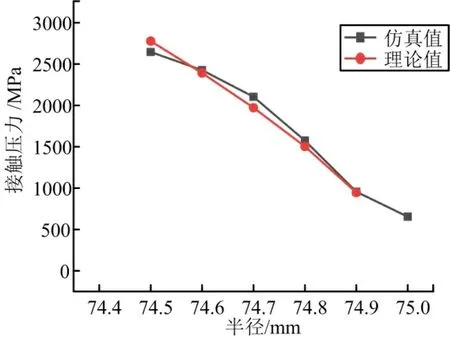
图3 接触压力与半径的变化关系Fig.3 The Relationship between Contact Pressure and Radius

4.2 球头半径对温度分布的影响

球头-球窝配合球面半径标称值为75 mm，球头半径变化导致接触状态的改变，通过仿真计算出了转动频率5 Hz 状态下，结构温度随时间变化规律，如图4所示。由图4 可以看出，随时间变化，结构温度逐渐升高；球头半径越小，结构温度越高，说明球头与球窝的匹配性越差。通过仿真结果对参数进行标定，标定结果为 γ = 0.001。

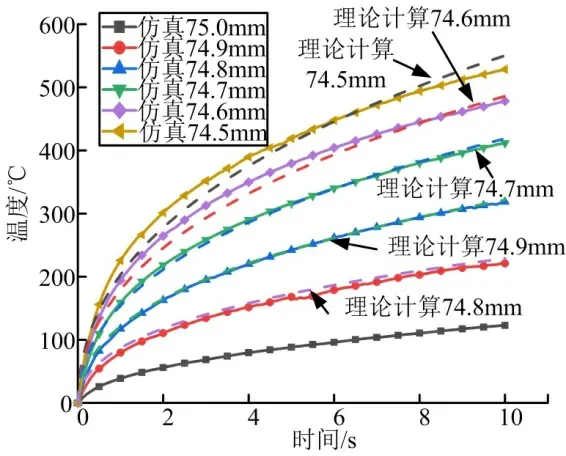
图4 不同球头半径结构温度变化曲线Fig.4 Temperature of Structure with Different Ball Head Radii

图5 给出了球头半径分别为74.5～75 mm 状态下的球头-球窝的温度场云图。从图5 中可以看出，随着球头半径的减小，接触面积减小，温度分布区域减小，说明74.5 mm 时，球头-球窝接触面积较小，受热结构体积较小，故温度最高达到529 ℃。当球头半径为75 mm 时，温度基本均匀分布于整个接触球面上，最高温度为136 ℃，温度相对于其他较低。当球头半径为74.9 mm 时，最高温度为212 ℃，整个球面的温度都上升，但温度不再均匀地分布于接触球面上，呈现中心温度高，边缘温度低，与75 mm 球头相比，球头半径为74.9 mm 时，边缘温度为92 ℃，当球头半径为74.7 mm，球窝边缘的温度未发生变化，这是由于此时球窝边缘不与球面接触，同时球头-球窝内部产生的热由于时间太短也无法传到其边缘处。

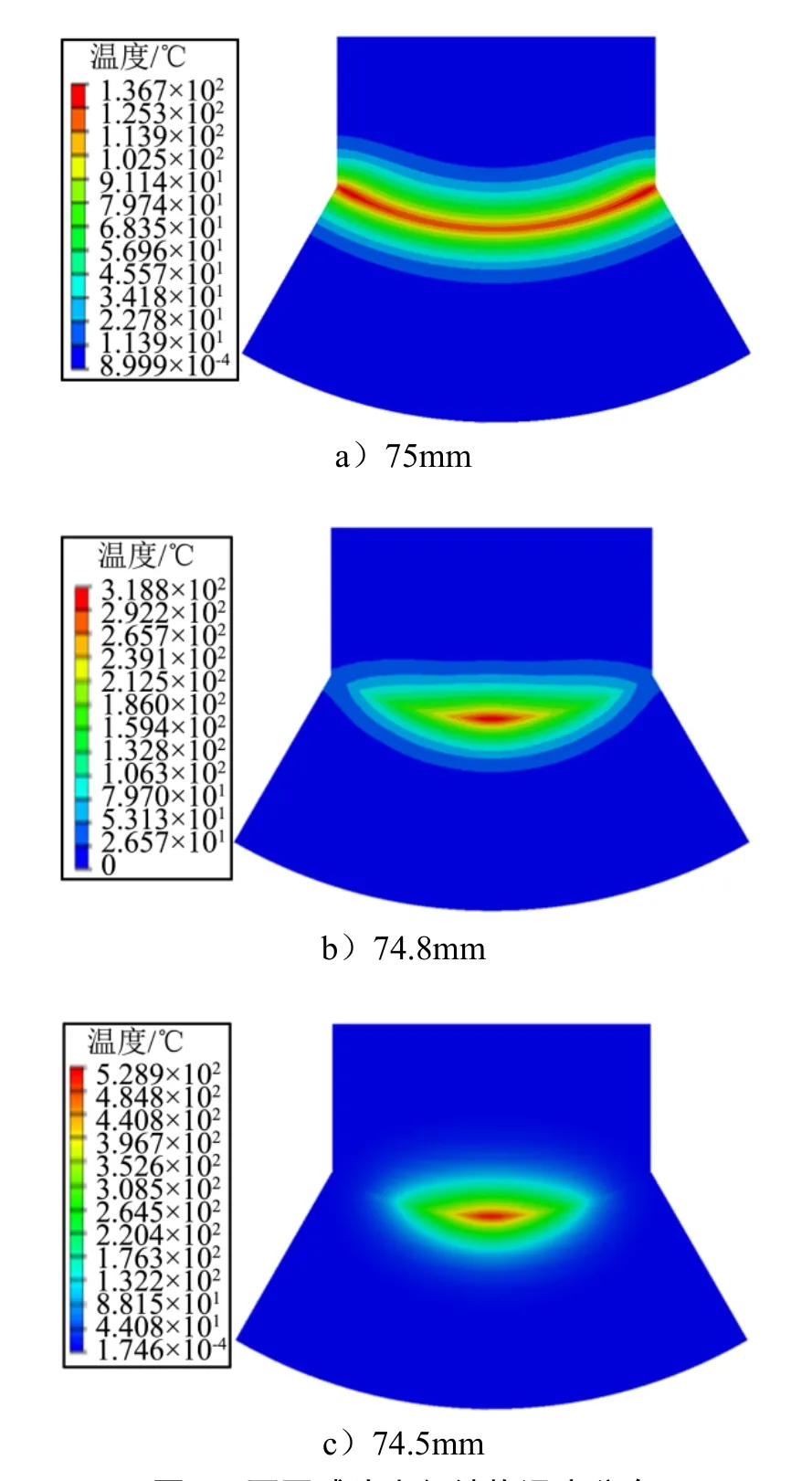
图5 不同球头半径结构温度分布Fig.5 Temperature Distribution of Structure with Different Ball Head Radii

4.3 转动频率对温升的影响

针对不同的转动频率，通过仿真计算出了球头半径变化对结构最高温度的影响规律，如图6 所示。由图6 可以看出，频率越高，结构温度越高，尤其在频率较高的情况下，配合半径对结构温度影响更加显著。

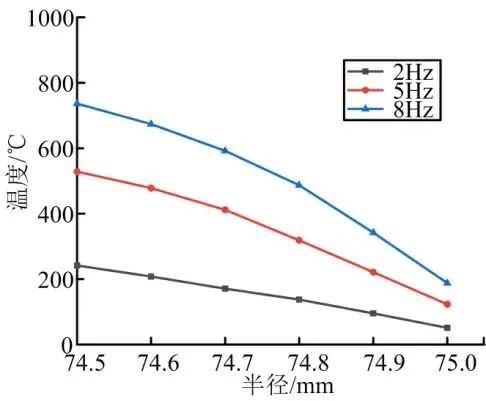
图6 不同频率下球头半径对温升的影响Fig.6 The Influence of Ball Head Radius on Temperature Rise at Different Frequencies

4.4 接触面摩擦系数影响分析

接触面摩擦系数直接影响摩擦生热总量及结构温升，合适的摩擦系数是确保结构正常工作的必要条件。对摩擦系数的要求，直接影响接触面润滑方案的选择。球头-球窝标称配合半径的状态下，通过仿真计算，获取了不同摩擦系数状态下，结构最高温度的变化规律，见图7。

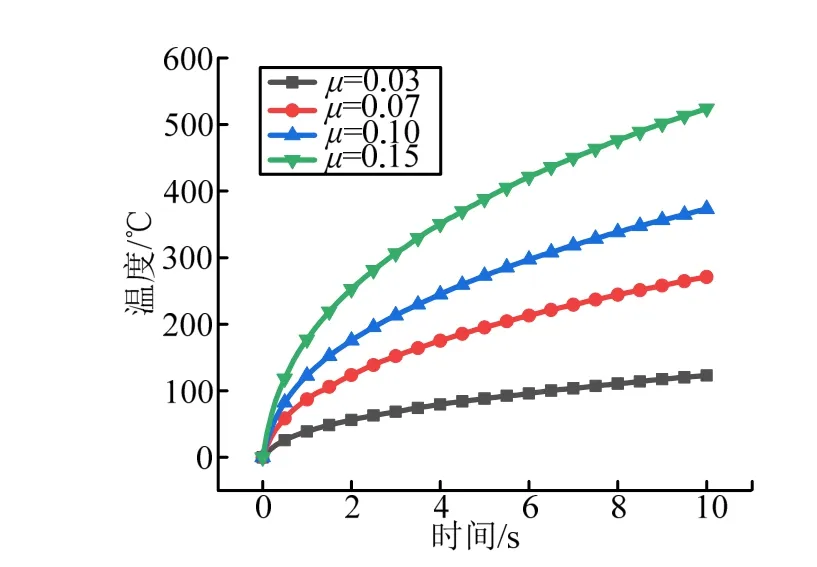
图7 不同摩擦系数下的温度随时间变化Fig.7 The Temperature Changes with Time under Different Friction Coefficients

由图7 可以看出，随着摩擦系数的升高，结构温度也在升高，摩擦系数为0.15 时，结构最高温度达到了500 ℃，大幅降低了结构强度。若将温度控制在150 ℃范围内，则摩擦系数应不大于0.03。

4.5 转动摩擦温升对应力分布的影响

在球头半径为75 mm 时，由于集中载荷的作用，球窝结构发生了变形，应力集中在球窝边缘处，为590 MPa。随着球头半径减小，施加集中载荷后，最大应力点出现在球窝中心，在球头半径为74.9 mm 时，最大应力为645.2 MPa，随着半径的增加，球窝中心的应力逐渐增加。

由于结构应力是衡量结构承载能力的重要指标，通过仿真计算，给出了结构最高应力随时间变化曲线，见图8。由图8 可以看出，球头半径为74.5 mm 和74.6 mm 时，结构最高应力随时间增加而减小。这是因为球头-球窝摩擦生热导致结构温度升高，改变了材料的强度特性，在球头半径为74.5 mm 时，由于结构温升较快，且结构温度较高，使得结构应力很快超出了屈服强度，进入了塑性区域，失去了承载能力。

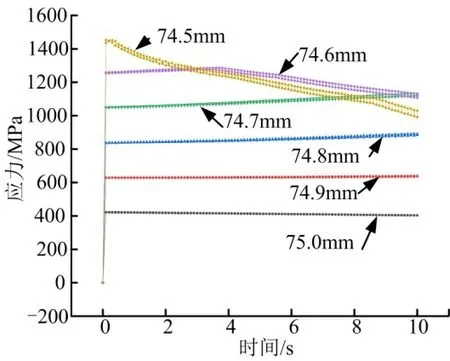
图8 摩擦过程中应力的变化Fig.8 Stress Changes during Friction

5 三向载荷作用下结构强度分析

根据三向载荷值的特点可知，转动摩擦生热主要来源于轴向载荷的作用。对上述有限元计算模型，在下端施加随时间变化的轴向载荷Fz，计算在2 种摩擦系数条件下（C01 状态为摩擦系数0.15，C02 状态为摩擦系数0.03），转动摩擦时间为148 s 时，模型的最大温度随时间的变化情况，结果如图9 所示。

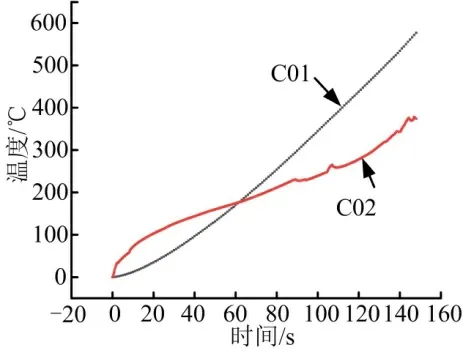
图9 转动摩擦生热温度变化Fig.9 Temperature Changes of Rotating Friction Heat

根据上述温度的变化以及材料-温度的模型，将C01 和C02 两种状态下转动摩擦温度变化导致的材料弱化等效为不同载荷下的材料参数，即材料强度参数会随着载荷的变化而变化。计算结构在三向载荷作用下的应力分布如图10 所示。

图10 C01、C02 状态下应力分布云图Fig.10 Stress Distribution Nephogram in C01 and C02 State

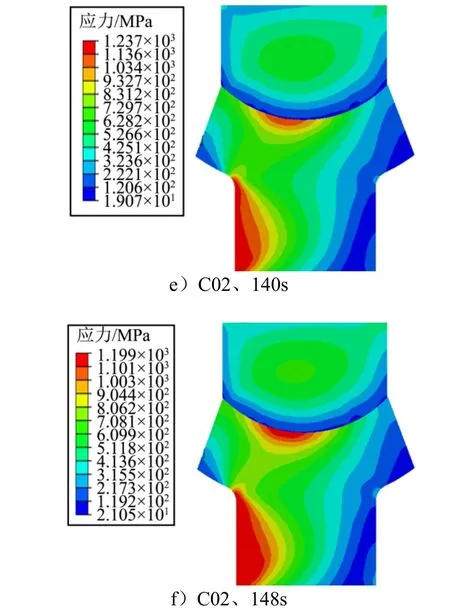
续图10

根据图10 的应力显示结果，可以分析得到，在C01 状态下，当连续变化的载荷增加到109 s，最大应力为1163 MPa，此后随着时间的增加，温度不断升高，导致材料的力学参数发生变化，应力迅速减小，材料出现了严重的变形，当加载时间到达145 s，结构已经发生了严重的变形，此时计算已经不能收敛，说明结构已经完全失稳。在C02 状态下，当连续变化的载荷增加到120 s 时，此时结构最大应力为1294 MPa，此后随着时间的增加，应力减小。与C01 状态相比，C02在加载时间到达148 s，捆绑结构仍能保持其稳定性。

图11 显示了球窝与球头接触位置的接触压力和材料强度随加载时间变化曲线。

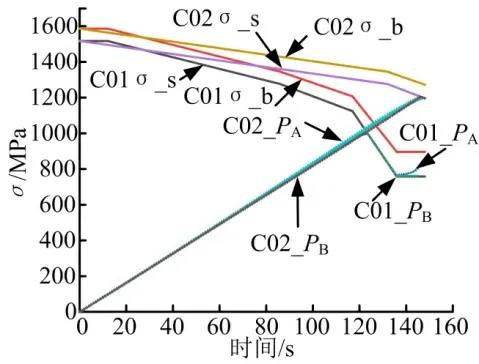
图11 A 点和B 点的应力变化Fig.11 The Change in Stress at A and B

图11 中A 点表示球窝一侧，B 点表示球头一侧。在C01 状态下，在0～123 s 内，A 点和B 点接触压力随着连续载荷的加载时间增加而增加，在118 s 时材料强度随着加载时间增加而迅速减少，当加载时间为145 s 时，结构完全失稳。在C02 状态下，在0～146 s 内，A 点和B 点接触压力随着连续载荷的加载时间增加而增加，虽然材料强度减小，但仍能保证结构的稳定性。在C01 状态下，结构承载能力仅为总载荷值的84%。

6 结 论

本文对球头-球窝配合的捆绑结构，建立求解接触压力和温升变化的理论计算模型，并通过有限元数值仿真，分析了不同半径差的球头-球窝配合下，由于转动摩擦生热导致温升变化，并与理论模型进行了对比。最后，对考虑转动摩擦生热的捆绑结构进行了强度分析研究。通过以上分析研究可以得到下述结论：

a）建立了能够描述接触压力和温升变化的理论模型，其中包含计算平均压力的面积修正参数ε ，以及计算温升变化时，用于修正温升区域的等效材料质量参数α 和修正热散失项的参数γ ；

b）球头-球窝配合状态对摩擦生热和接触面压力影响较大，球头与球窝半径相差较大时，结构温升较大，接触面压力较大，设计过程中，应严格控制球面配合尺寸；

c）接触面摩擦系数对结构温升影响较大，在没有润滑方案的情况下，结构温升过大，因此，对于传递较大载荷的传力机构，应选择较好的润滑方案，保证较低的摩擦系数，控制结构温升。