一年级学生“反向等式”掌握情况调查分析
□曾根红
“反向等式”是相对于“正向等式”而言的。把运算符号在等号左边、结果在等号右边的等式称为“正向等式”,如8+7=15;把运算符号在等号右边、结果在等号左边的等式称为“反向等式”,如15=8+7。
一年级学生对正向与反向的计算题掌握情况如何,是否达到了教学要求?笔者展开了调查,本文阐述调查的过程与结果。
一、调查的对象与方法
1.调查对象:江西省某农村中心小学一年级学生49人(一个班级)。
2.调查方法:问卷调查(书面测试)和访谈;发出问卷49份,收回有效问卷49份。
二、调查的内容与意图
笔者设计了28道测试题,主要分为四类:
①给出正向与反向等式,要求学生直接写出计算结果。如37+8=()、()=37+8,试图测试学生在解决正向与反向等式正确率上的差别。
②给出正向与反向等式,要求学生写出被减数或减数。如()-7=8、7=12-(),试图了解学生对加减法各部分关系的掌握情况及在解决正向与反向等式时的差别。
③给出正向与反向等式的单一开放题,要求学生在一个等式中,填写多种不同的答案。如13=()-()、57=()+();试图了解学生在解决这类问题时的差别。
④给出反向的连等式,要求学生填写每一个等式中的答案,如16=()+()=()+()=()+()。试图了解学生有序思考的能力。
测试时题目并不是按类出现的,而是全部打乱给学生做。在学生完成书面测试后,笔者选择了部分学生进行访谈,访谈的主要问题有:这个题目是什么意思?这个题你做得很好,你是怎么想的呢?为什么在这里填这个数?这个测试题难不难?你觉得哪里比较难?这个题你做错了,你知道为什么错了吗?
三、调查的结果与分析
(一)对比出现的正向与反向等式计算结果的正确率及分析
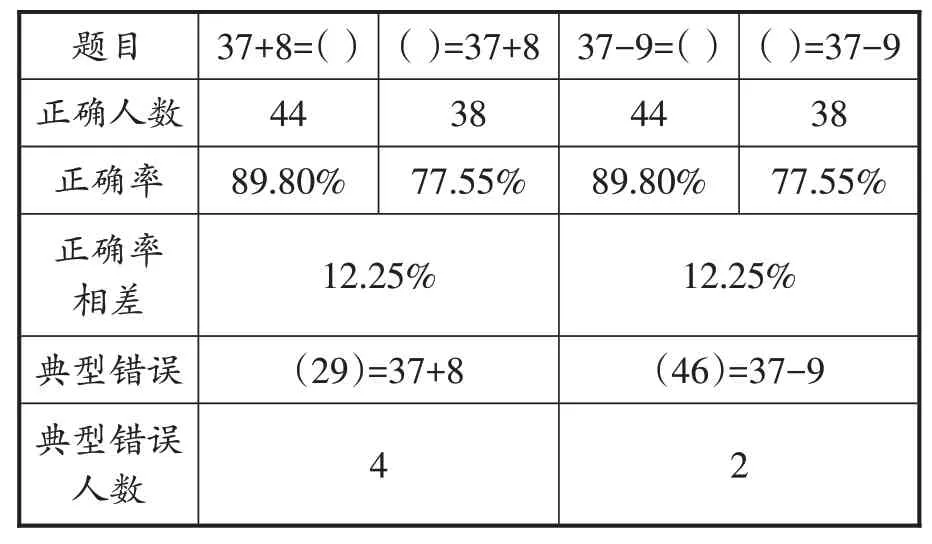
表1 对比出现的正向与反向等式正确率统计表
从表1可以看出:
(1)无论是加法还是减法,正向等式的正确率都比反向等式的正确率高12.25%。这说明部分学生在解决反向等式时,并没有认识到正向等式与反向等式在意义上是相同的,从而得到相同的结果。也就是说,他们不能从正向等式的结果中,得到相应的反向等式的结果。学生反向等式接触少,教师在教学中没有引起足够的重视是一个重要的原因。
(2)无论是加法还是减法,正向等式的正确率都不到90%。这说明所调查的农村小学学生的整体素质还比较低,没有达到课程标准的要求。教学中还需要让学生更好地明确算理,掌握方法,并能熟练地计算。
通过访谈发现,在反向等式的两种典型错误中,一部分学生对于等号的理解还停留在“左边加出来(或减出来)的结果等于右边”这样的认识上。学生还是试图用“()+8=37”这样的正向等式来得到反向等式“()=37+8”括号里的数。在解决减法的反向等式时,学生也反映出类似的思维过程。另一部分学生在解决反向的加法算式()=37+8时,运用了减法37-8,得到括号中的数29,这里学生并不是把加号误看成了减号,而是觉得“等式反过来了,加法也反过来变成减法了”。
以上结果说明,在平时的教学中,对于等号表示平衡的意义需要加以强调;对于反向等式的意义也需要让学生进一步理解。
(二)在反向等式中,学生填写被减数或减数的结果与分析

表2 反向等式中填写被减数与减数正确率统计表
从表2可以看出:
(1)学生在解决8=()-7时,括号中填入1的比较多,主要原因是学生并不明白这个等式的意义,而是凭借他们看到的“8”“-7”以及在()里填数,就进行了“8-7=1”的计算,并把1填入括号中。通过访谈笔者还发现有个别学生试图计算7-8,由于不会减,所以改成8-7,这也说明学生对于算式意义理解存在缺失。有趣的是,部分学生虽然在括号里填上了正确数15,但思路是完全错误的,原因是在试卷中8=()-7这个题目前,出现了一道正向等式()-7=8,当学生见到反向题时,就认为应该把减变成加,计算7加8等于15,所以在括号里填上了15。这种巧合也是对意义不理解的反映。
(2)在解决7=12-()时,典型错误是7=12-(19),错误人数占总人数的20.41%。看到这答案一般人都认为是学生计算的“序”出了问题。但笔者通过访谈得知,多数错误学生的想法并非如此,他们是对已有元素重新组合,甚至改变元素进行计算,他们有着“顽强”的从左到右计算的意识,个别学生先试图用7减12,发现不行,就改为7加12,这样就得到了19。也有个别学生发现7-12不够减时,就改成12减7。这些学生又“巧合”正确了,但也反映出学生对于反向等式的意义完全没有理解。
(三)反向连等式的调查结果及分析
1.反向连等加法算式。

表3 反向连等加法算式正确率统计表
这是一个答案不唯一的问题,要求学生填出三组答案,每组两个数的和都是16。如果把从左到右的顺序分别称为第一、第二、第三组数的话,那么,从表3中可以看出,填出第一组数的正确率远高于第二与第三组数,说明部分学生对于连等式的意义是不理解的。学生的错误主要有以下三类:
(1)把前一组数中的后一个数作为和,写出下一组数(见错例1)。

错例1
笔者通过访谈得知,学生把这道连等加法算式看成三道独立的加法算式,受第一组数16=()+()的影响,产生类似6=()+()这样的算式,并进行解决。
(2)不能运用“解决反向等式的思路”,而是受解决正向等式的思维习惯的影响,填出括号内的数(见错例2)。

错例2
最后出现的10,是从第一个数10中抄写过来的。说明这些学生完全没有理解这个题目的含义。
(3)从右往左计算。即学生看到反向等式时,就从右往左考虑,先确定最右边的一组数相加是16,然后像上面第(2)种错误类型那样思考问题(见错例3)。
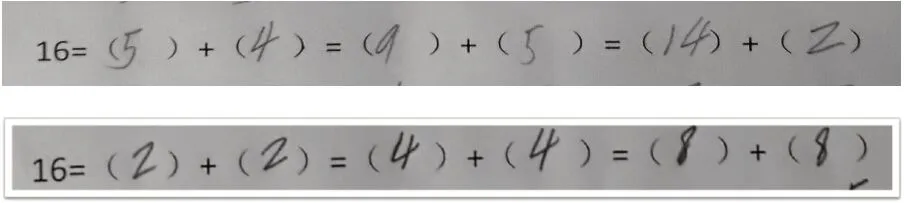
错例3
2.反向连等减法算式。

表4 反向连等减法算式正确率统计表
从表4可以看到,学生解决反向连等减法算式的正确率比较低,比解决反向连等加法算式的正确率还要低。笔者通过访谈得知,学生出错的类型以及错误的解题思路与上文中已经分析的基本一致,这里不再重复阐述。
四、结果与建议
(一)结果
1.学生解决反向等式的正确率明显低于正向等式,教学中,教师要引起对反向等式教学的重视。
2.学生在解决反向等式的问题时,缺少对这类等式意义的理解和解决问题的思路,即学生不明白反向等式的含义,在解决反向等式的问题时缺少必要的解决问题的思路。
(二)建议
1.加强等号意义的教学。教师不仅要使学生知道左边的数相加(或相减)后得到右边的数,中间可以用等号连接,而且当左右两边的数或式相等时,也可以用等号连接。教师要帮助学生建立“等号是表示左右两边平衡的符号”的观念。
2.加强反向等式意义的教学。可以用直观图或实物(如运用天平)进行演示,让学生理解如16=()+()这样的算式表示天平的左边已经有一个物体重16,右边要放入两个物体,放入后才能使天平平衡,也就是要使右边的两个数加起来的和等于16。
3.重视解决反向等式问题的思维过程。如在解决16=()+()时,可以让学生结合天平想:16可以分成几与几。几和几合起来是16;也可以先在一个括号里填入一个数,比如6,然后想,再填多少可以使得这个数与6相加的和是16。这样的思维过程分析,会让学生有规律可循。
4.要进行加法和减法的正向与反向等式的对比,在对比中明确异同,逐步引导学生克服总是用正向等式的思路解决反向等式问题的思维习惯。
(本文在研究过程中,多次得到朱乐平老师的悉心指导,在此表示衷心感谢!)

