削减轮数的Khudra-64 积分攻击*

李艳俊 梁 萌 林 昊 袁 峰

北京电子科技学院，北京市 100070

引言

随着物联网技术的不断发展，体积小、资源受限的设备的日渐普及对密码算法提出了新的要求。 在资源有限的条件下，轻量级分组密码既能够有效地提供安全性保障，又能实现较好的运行效率，能够很好地满足物联网技术发展对密码技术的要求。 近年来，有很多的轻量级分组密码被 提 出， 如 Midori[1]、 Piccolo[2]、 MIBS[3]、 等。Khudra[4]算法是由Souvik Kolay 等人于2014 年提出的总轮数为18 轮的轻量级分组密码算法。

积分攻击[5]、差分攻击[6]、线性攻击[7]是目前最主要的三种密码分析方法，用来对密码算法进行安全性的评估。 积分攻击通过分析加密过程中积分性质的传播变化过程，确认区分器的活跃比特、常数比特和平衡比特的位置，进行积分区分器的构建。 利用得到的积分区分器的性质，可以以更好的时间和数据复杂度，对密码算法进行更多轮数的密钥恢复攻击。

近年来，自动化搜索技术的提出与不断发展，也进一步推动了密码分析领域的发展。 区分器的搜索和构建也更加便捷。 向泽军[8]等人在Todo[9]提出的可分性的基础上，进一步与MILP思想结合，提出来基于比特可分性的MILP 积分区分器搜索技术，能够更加方便高效地对密码算法的积分安全性进行评估。

密钥恢复攻击是一种常见的密码算法安全性分析方法。 其主要思想是，利用密码算法的某些固有特性规律或设计缺陷，通过某些巧妙的操作和处理，使得最终能够获得加密过程中某些密钥比特的信息素。 本文利用搜索得到的积分区分器，对Khudra-64 算法进行了9 轮，10 轮和11轮的密钥恢复攻击。 对Khudra-64 在积分安全性方面进行了较为完善的总体评估。

1 预备知识

1.1 Khudra 算法介绍

Khudra 算法是由Souvik Kolay 等人于2014年针对FPGAs 环境提出的对称分组加密算法，在软硬件实现中都具有较好的表现，同时也能够较好地抵抗各种密码攻击方法。 Khudra 算法的分组长度为64 比特，主密钥长度为80 比特，共进行18 轮加密，在第一轮与最后一轮加密时需要加入白化密钥。

算法中的F 函数的结构与算法的加密结构较为相似，是一个循环6 轮的Feistel 加密结构。F 函数为16 进16 出的加密部件，当F 函数的输入为x[1，16]，输出为y[1，16]， 则输入和输出之间有如下关系:

y[1，4]＝Sbox(Sbox(Sbox(Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12]) ⊕Sbox(x[9，12]) ⊕x[13，16])

⊕Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕Sbox(Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕x[5，8]

y[5，8]＝Sbox(Sbox(Sbox(Sbox(Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12]) ⊕Sbox(x[9，12]) ⊕x[13，16])

⊕Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕Sbox(Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕x[5，8])

⊕Sbox(Sbox(Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕Sbox(x[1，4]) ⊕x[5，8])

⊕Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12]

y[9，12]＝Sbox(Sbox(Sbox(Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕Sbox(x[1，4]) ⊕x[5，8])

⊕Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12]) ⊕Sbox(Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12])y[13，16]＝

⊕Sbox(x[9，12]) ⊕x[13，16]

Sbox(Sbox(Sbox(Sbox(Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]) ⊕Sbox(x[1，4]) ⊕x[5，8])

⊕Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12]) ⊕Sbox(Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12])

⊕Sbox(x[9，12]) ⊕x[13，16]) ⊕Sbox(Sbox(Sbox(Sbox(x[1，4]) ⊕x[5，8]) ⊕x[9，12])

⊕Sbox(x[9，12]) ⊕x[13，16]) ⊕Sbox(Sbox(x[9，12]) ⊕x[13，16]) ⊕x[1，4]

1.2 基于比特可分性搜索获得的积分区分器

可分性是由Todo 提出的一种广义的积分性质，可以用来帮助评估分组密码的积分安全性。向泽军等人在此基础上，利用MILP 方法进行可分性的建模，对几种常见的密码算法进行搜索，均成功地获得了较好的区分器结果。 在此前的文章中，已经通过对Khudra 算法进行MILP 建模搜索得到了两个6 轮积分区分器和一个7 轮区分器。 通过搜索得到的7 轮积分区分器如下:

输入:(ccccccccaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaa)

输出:(??????????????????????????????????? b????????????????????????????)

在上述的积分区分器中，a 表示在输入的明文集中，该位置为活跃位置，取值需要取遍0 和1。 c 表示在输入的明文集中，该位置为常数位置，取值可以为0 或1，但所取值需要保持不变。b 表示经过7 轮加密之后输出结果的平衡位置。将明文集对应的加密结果的平衡位置的值进行异或后，值必然为0。? 表示输出结果中的未知位置，这些位置的性质难以确定，不具有规律性。

该区分器所代表的的含义为:将输入的第9到64 位设定为活跃比特位，取相应的明文集进行7 轮加密之后，加密结果密文集求和后的第36 位比特为平衡位置，值为0。 本文的攻击是基于搜索到的上述7 轮积分区分器进行的。

2 积分攻击

取符合区分器的输入的明文集。 将常数比特位设为定值，取遍所有活跃比特位的所有的值，遍历后得到攻击所需的明文集。 明文集内共有256个不同的明文。 在攻击中的一些符号所表示含义如下:

rkxi: 第x 个子密钥中的第i 比特的值。rkx[i，j]:第x 个子密钥中的第i 到第j 比特的值。

A＝B:可以从B 的值中推得A 相应的比特的值。

2.1 Khudra 算法的9 轮密钥恢复攻击

将明文集进行9 轮加密，取加密结果的第4位比特，第49 到64 位比特的值，攻击过程如下:

CT扫描需要较长的时间，这个过程中，扫描对象如果发生形状、位置的变化，会降低CT成像质量。运动伪影主要分为刚体运动伪影和非刚体运动伪影。

将加密结果的第49 到64 位比特的值代入F 函数中，可以推得:

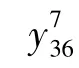
2.2 Khudra 算法的10 轮密钥恢复攻击

将明文集进行10 轮加密，取加密结果的第52 位比特，第17 到48 位比特的值，攻击过程如下:

根据Khudra 算法的细节可以推得:

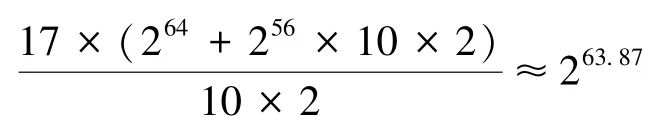
2.3 Khudra 算法的11 轮密钥恢复攻击

将明文集进行11 轮加密，取加密结果的第36 位比特，第1 到32 位，第49 到64 位比特的值，攻击过程如下:

根据Khudra 算法的细节可以推得:

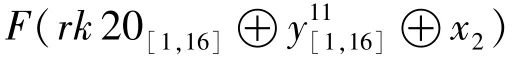
在整个攻击过程中，共需要猜测34 比特的密钥值。 需要34 个特定的明文集，才可以得到唯一正确的

3 结论

在基于比特可分性进行MILP 建模搜索得到的7 轮积分区分器的基础上，使用部分和技术，对Khudra-64 算法进行了9 轮，10 轮和11轮的积分攻击。 9 轮积分攻击的时间复杂度为256.08次9 轮加密，数据复杂度为256。 10 轮积分攻击的时间复杂度为263.87次10 轮加密，数据复杂度为260.09。 11 轮积分攻击的时间复杂度为280.63次11 轮加密，数据复杂度为261.09。 算法的主密钥为80 位比特，在9 轮，10 轮积分攻击中，时间复杂度优于穷搜攻击，在11 轮攻击中，时间复杂度基本与对主密钥进行穷搜攻击相等。 这是首次较为全面的对Khudra-64 的积分性质评估。

迄今为止，很多作者对Khudra 算法进行了安全性评估。 在参考文献[16]和[17]中，分别做到了16 轮的相关密钥矩形攻击和全轮的相关密钥不可能差分攻击。 在16 轮的矩形攻击中，时间复杂度为278.7， 数据复杂度257.82；全轮的不可能差分攻击的时间复杂度为268.5， 数据复杂度263。 综上，两种攻击的轮数比我们的积分攻击轮数要长，复杂度也基本优于我们的积分攻击。 由此可见，Khudra-64 算法结构在抵抗积分性评估时表现更好，也就是说，Khudra-64 能够较好地抵抗可分性方面的自动化搜索和密钥恢复攻击，具有较好的积分性质，为算法设计提供了一定的思路。