泰勒公式在高等数学课程教学中的案例设计*

张艳硕 常万里 李万玉 冷 南

1. 北京电子科技学院，北京市 100070；

2. 北京电子科技学院，北京市 100070

引言

泰勒公式是把函数用多项式近似表示的重要依据，是高等数学课程中的重要内容，探讨泰勒公式在函数的极限求解、导数应用、近似计算和级数的敛散性判断等方面应用在高等数学课程学习中具有重要意义。

泰勒公式，于1715 年布鲁克·泰勒发表的《Methodus Incrementorum Directa et Inversa》[1]一文中首次提出，约瑟夫·拉格朗日将其称之为“导数计算的基础”，并由此开创了有限差分理论。 泰勒公式广泛应用于数学、物理及其他领域，是一个用函数在某点的信息描述其附近取值的公式。 在高等教育出版社的《高等数学》第三章[2]中重点讲解了泰勒公式及其相关内容。

在高等数学中，解决数学问题常常需要进行有限和无限的相互变换，这是泰勒公式存在的重要意义，通过认识这种函数展开与向量空间的联系可以更深的理解函数的微分学，成为解决数学问题强有力的工具。

本文旨在探讨泰勒公式在高等数学课程教学中的典型设计与应用实践。 文章将首先从泰勒公式在实际教育教学中的前置工作进行总体概括，其次从极限、导数和积分学方面以经典案例对泰勒公式进行典型教学设计，在总结归纳知识基础的同时建立知识体系。 在实际教学过程中注重逻辑推理及知识迁移能力，明晰证明思路、加强思辨能力、精准挑选例题并体现知识应用，为学生在今后高等数学课程学习做好铺垫、开拓思路并打下坚实基础。

1 泰勒公式及其扩展形式

泰勒公式[3]，也称泰勒展开式，是用一个函数在某点的信息，描述其附近取值的公式。 如果函数足够平滑，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以利用这些导数值用以做系数，构建一个多项式近似函数，求得在这一点的邻域中的值。 多项式函数是一种简单而又基本的函数，具有形式简单的表达式和很好的分析性质。 泰勒公式是把函数用多项式近似表示的重要依据，利用该公式可以把对复杂函数的研究转化为一个多项式来处理。

麦克劳林(Maclaurin)公式是泰勒公式(在x0＝0，记ξ ＝θx(0 ＜θ ＜1) 时)的一种特殊表现形式，通过对泰勒中值定理的研究，其扩展形式，带有佩亚诺余项及带有拉格朗日余项的麦克劳林公式在高等函数极限与不等式研究当中有着极为广泛的应用。

2 泰勒公式教学前置

前置性教学是生本教育理念的重要表现形式，可以有效衔接前置性学习与课堂教学。 泰勒公式集中体现了微积分“逼近法”[4]的精髓，泰勒公式的使用可以简化数学运算，并且可以满足高精度的计算。 多数学生在初识高数课程时，其认知能力和逻辑思维大多都停留在高中阶段，脑海中没有明晰的连续和逼近等概念。 泰勒公式利用多项式来逼近函数，具有形式简单、易于理解和易于计算等优点。 通过对泰勒公式以及其扩展形式的进一步学习，为学生在高等数学在极限、微分和积分等方面的学习打下了坚实基础，极大提升了学生在高数课程学习中的理解能力。我们将从无理数逼近计算、复变函数及其他方面进行深入阐述。

2.1 无理数的逼近计算

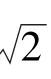
此题利用3 阶泰勒公式求解的一般步骤为:

由此可见，我们可以利用泰勒公式可以实现无理数的逼近计算并可以利用余项估计其误差。

2.2 泰勒公式在复变函数中的典型应用

欧拉公式[6]是将复指数函数与三角函数相联系的一个公式，eix＝cosx ＋isinx，e 为自然对数的底，i 为虚数单位。 欧拉公式将指数函数的定义域扩大到复数范围，并建立三角函数和指数函数的关系，在数学分析、复变函数论里也占有非常重要的地位，更是被誉为“数学中的天桥”。下面我们应用不带有余项的麦克劳林公式去验证欧拉公式。

验证欧拉公式:eix＝cosx ＋isinx

将上面的b 换成x，便得到了欧拉公式。 由欧拉公式，对任意一个复数z ＝ib，有

ea＋ib＝eaeib＝ea(cosb ＋isinb)

即复数z 的指数函数依然是一个复数，这个复数的模r ＝ea， 幅角θ ＝b。 若b ＝0， 则ez＝ea(cos0 ＋isin0) ＝ea，与实变函数f ( x) ＝ex在x＝a 时的函数值相同。

由此可见，我们可以利用泰勒公式实现在数学分析、复变函数论中的相关应用。

3 教学设计

泰勒公式[7]比较抽象，难以理解，学生一般很难吃透泰勒公式的实质，更难以实现对公式的灵活运用。 因此，泰勒公式一直是高等数学教学过程中的一个难点问题。 为使学生能够更好的理解泰勒公式思想，我们分别对极限问题、导数问题以及积分学问题进行典型案例教学设计。

3.1 基于泰勒公式的极限问题案例教学

极限是高等数学中的重要基础概念，连续、微分和积分等基本概念都是建立在极限概念的基础之上。 等价无穷小代换和洛必达法是学生们常选用的两个方法，但两种方法都具有一定的局限性。 等价无穷小代换只能用于乘、除因子，在用作加、减项的无穷小量时，则不能随意用其等价无穷小进行替换。 应用洛必达法则会造成有些函数求导十分繁琐，多次应用洛必达法则会使计算量增大。 此时，一般可以利用泰勒公式解决极限问题。

(1)关于极限证明的典型设计

泰勒公式在极限证明题的应用，常常会有化繁为简，化难为易的效果，下面我们以一道经典极限证明问题为例，讨论泰勒公式在极限证明中的具体应用。

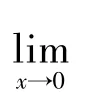
学生有时并不清楚利用等价无穷小sinx ～x，tanx ～x 解题时会造成分子、分母不同阶，进而得出原式为0 的答案。 利用泰勒展开式可以巧妙地解决这一困惑，由带有佩亚诺型余项的麦克劳林公式

通过应用泰勒公式，能够加深学生对于等价无穷小在实际做题中的理解与应用，在解决极限计算问题中进一步深刻体会高等数学中的“逼近”思想。

(2)关于极限计算的典型设计

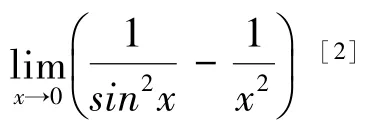
通过泰勒展开式的运用，我们可以清晰地看出，若步骤一或步骤二中使用等价无穷小x ～sinx 会因分子所忽略的余项影响计算结果，进而造成计算错误。 泰勒公式通过构建一个多项式近似函数，使得计算简化。

(3)利用泰勒公式求极限问题的注意事项

b)极限形式为f ( x) - g ( x) 时，将f ( x) ，g ( x) 分别展开到能令他们的系数不相等的最低次幂。

3.2 基于泰勒公式的导数问题案例教学

泰勒公式[8]在微分学中的应用极为广泛，在解决计算、证明问题时既十分方便又有规律可循。 一般地，对于题设条件中含有或蕴含有“函数具有二阶或二阶以上导数”的题型，都可考虑应用泰勒公式。

(1)关于导数计算的典型设计

在解决导数计算一类问题时，特别是在函数有多阶导函数时可以利用泰勒公式来进行证明。下面我们以一道典型导数计算问题为例，集中展示泰勒公式在导数计算中的具体应用。 设f(x)在[0，1] 上具有二阶连续的导数，f(0)＝f(1)＝0 且当x ∈(0，1) 时， ｜ f″(x) ｜≤2， 试证: ｜f′(x) ｜≤1。

证明:因为f(x) 在[0，1] 上具有二阶连续的导数，因此，f(x) 的一阶泰勒展开式存在

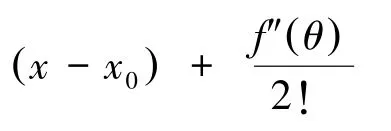
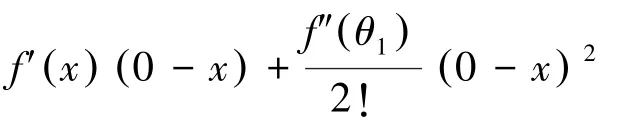
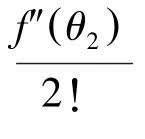
其中， θ1介于0 与x 之间， θ2介于x 与1之间。

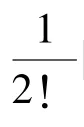
通过上述证明可以看出，关于导数计算的泰勒公式在不等式的证明过程中起到了非常关键的作用。

(2)关于导数综合题的典型设计

在导数的综合应用方面熟练应用泰勒公式及其扩展形式麦克劳林公式、拉格朗日中值定理，有着极大的实用性和便捷性。 下面我们以一道根的唯一存在性的典型例题进行说明。 设f(x) 在[a， ＋∞) 上二阶可导，且f(a) ＞ 0，f′(a) ＜0，对x ∈(a， ＋∞)，f″≤0，运用泰勒公式证明: f(x) ＝0 在(a， ＋∞) 内存在唯一实根。

因为f″(x) ≤0， 所以f′(x) 单调减少，又f′(a) ＜0，因此x ＞a 时，f′(x) ＜f′(a) ＜0，故f(x) 在(a， ＋∞) 上严格单调减少。 在a 点展开一阶泰勒公式有

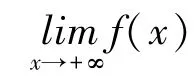
由简到繁，由特殊到一般，是理解泰勒公式这类抽象理论知识的极好方式。 本题通过巧妙的应用泰勒公式，极大地提升了解题速度和准确性。

(3)利用泰勒公式求导数问题的注意事项

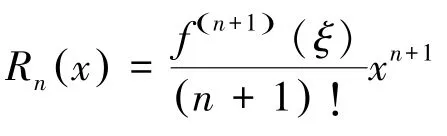
3.3 基于泰勒公式的积分学问题案例教学

泰勒公式在积分学中有着广泛应用，在解决精确计算、不等式证明和积分敛散性判断等问题时能够做到化繁为简，化陌生为熟悉，化复杂为简单的作用。

(1)关于不定积分的典型设计

设f ( x) ＝x3＋x2＋x ＋1，将函数f ( x) 在x ＝1 点展开，有

从解题过程不难看出，利用泰勒公式免去了因为利用待定系数所带来的繁杂运算，减少了错误发生的可能，进而简化运算。

(2)关于定积分精确计算的典型设计

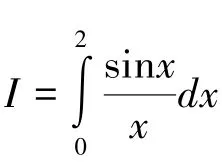
(3)关于广义积分有限区间敛散性判断的典型设计。

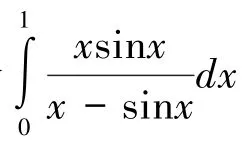
(4)关于广义积分无限区间敛散性判断的典型设计

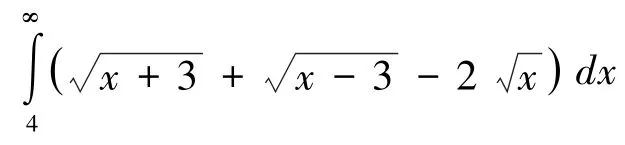
在对某些正项级数的敛散性的判定时，我们可以利用比较判别法，也可以利用比值判别法的极限形式，但是有些时候，泰勒公式是一个很好的桥梁，以实现级数的敛散性判定。

(5)利用泰勒公式求积分学问题的注意事项。

a)在解决有关泰勒公式的积分学问题时，应注意区分不定积分，定积分的实际应用；

b)在解决有关广义积分的敛散性判断问题时，应注意区分积分有限区间，无限区间的差异；

c)在解决某些具体题目时，泰勒公式不一定是最简便的做法。 应做到具体问题具体分析，灵活运用泰勒公式。

4 泰勒公式的广泛应用

泰勒公式是解决高等数学中许多问题的重要工具，众多复杂的数学问题，利用泰勒公式可以得到更加简便快捷的解决。 由于某些数值计算和理论分析的需要，对于一些稍微复杂的函数，我们经常需要用一些合适的多项式，即相对简单的函数来对原函数进行近似表示，泰勒公式[11]便是其中精确度比较高的一种。

泰勒公式在近似计算上有着独特的优势[12]，利用它可以将非线性问题化为线性问题，并能满足很高的精确要求，其在微分学相关计算与证明实例中的应用方法，借助泰勒公式解决问题更高效便捷。 带有佩亚诺余项抑或是带有拉格朗日余项的麦克劳林公式可应用于高阶不等式[13]的证明。 利用常见函数的泰勒公式，可以大大简化函数形式，求解时方便快捷。 还可以利用泰勒公式求极限问题，导数问题，利用泰勒公式求初等函数的幂级数展开式，方程根的存在性证明，级数的敛散性判断和方程的近似求解等等。 对于某些求不定积分的题型，若采取泰勒公式，将极大简化解题过程。

同时， 泰勒公式[14]在其它学科中也有着广泛而深远的应用.例如，在经济学风险评估、金融学中期望效用函数和均值-方差分析的关系、时间序列分析中的平稳化过程和弹性力学等方面都需要借助泰勒公式才能获得重要成果。

5 总结

在高等数学中，解决数学问题常常需要进行有限和无限的相互变换，这是泰勒公式存在的重要意义，通过认识这种函数展开与向量空间的联系可以更深的理解函数的微分学，成为解决数学问题强有力的工具。 我们深入探讨泰勒公式在分析和研究数学问题等方面的应用，在对于解决一些复杂的数学问题时，常常可以起到事半功倍的效果。 在具体应用泰勒公式时，要具体问题具体分析，灵活应用泰勒公式。 在实际教育教学中，通过实例探讨泰勒公式在微积分学中的相关证明及计算中的诸多应用，令学生们体会到应用泰勒公式解决问题的便捷性与实用性。