GNSS观测数据ZTD建模的质量控制方法

丁君生，陈俊平，王君刚

(1. 中国科学院上海天文台，上海 200030； 2. 中国科学院大学天文与空间科学学院，北京 100049； 3. 德国地学中心，波兹坦14473)

0 引 言

电磁波信号在穿过大气层时受到气体分子的影响，被延迟和弯曲，从而使得测量距离产生偏差[1]。其中穿过电离层产生的偏差叫做电离层延迟，而穿过未被电离的中性大气(包含对流层和平流层)产生的偏差统称为对流层延迟[2]。电离层延迟可以通过双频差分技术基本消除，而对流层具有非色散性质，其延迟无法通过双频数据改正[3]。在全球卫星导航系统(Global navigation satellite system，GNSS)数据处理中，对流层延迟通常作为待估参数解算或通过模型进行改正[4]。

模型改正法可以分为两类，第一类是基于实测气象参数的对流层模型，如Saastamoinen[5](以下简称为Saas)和Hopfield[6]等，其改正精度可达厘米级或分米级[7]。由于这类模型高度依赖实测气象参数，且有学者发现这类模型计算的ZTD与经验模型相比精度上没有优势[8]，故而这类模型在实时导航中的应用偏少。第二类是基于对流层关键参量的经验模型，这类模型不依赖实测气象参数，使用方便，仅需提供时间以及测站信息，便能得到厘米级精度的ZTD。其中有基于标准大气模型参数的UNB系列模型[9]和EGNOS模型[10]，UNB3模型在北美区域估计的ZTD平均误差约为2 cm[11]，EGNOS总体精度与采用实测气象参数的Saas和Hopfield模型相当[8]。还有基于再分析资料的GPT系列[12-14]、TropGrid系列[15-16]和IGGtrop系列模型[17]，GPT模型基于欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)提供的数值天气模型(Numerical Weather Model，NWM)产品，可提供测站气象数据，然后采用Saas等模型计算ZTD，精度优于EGNOS、UNB3模型。TropGrid基于美国国家环境预报中心(National Centers for Environment Prediction，NCEP)的NWM产品建立，与EGNOS相比全球平均精度提高了25%[18]。IGGtrop模型基于美国国家环境预报中心(National Centers for Environment Prediction，NCEP)再分析资料建立，精度优于EGNOS、UNB3、UNB3m[17]。

参数估计法将ZTD作为未知参数参与GNSS定位解算，其将ZTD的主项，即天顶对流层静力学延迟(Zenith hydrostatic delay，ZHD)作为延迟的先验值，将天顶对流层湿延迟(Zenith wet delay，ZWD)作为ZHD的改正值[19]。参数估计法精度最高，可达毫米级[20]，但是受限于GNSS测站的分布，无法获得任意位置的对流层延迟估计。

随着GNSS站网的加密以及数据传输速率的提升，高空间分辨率的ZTD数据出现爆炸式地增长，部分学者开始采用一些机构解算的GNSS对流层延迟数据，建立对流层延迟模型。这类模型保留了经验模型不依赖实测气象参数、建模简单、使用方便和精度优良的优点，同时能够最大程度保证在GNSS应用中的自洽。文献[21]采用国际GNSS服务组织(International GNSS Survice，IGS)提供的对流层天顶延迟产品，建立了一种简单的全球对流层天顶延迟模型，全球范围内RMS为4.9 cm。受限于IGS测站数量不足，该模型并不精细。文献[4]利用上海天文台GNSS分析中心解算的陆态网对流层数据建立了中国区域对流层天顶延迟网格模型SHAtrop，该模型建模精细，精度良好。然而在整个模型的建立过程中，缺乏有效的质量控制手段，不能够给其他区域建立类似的模型提供很好的参考。同时，该模型在ZTD时间序列拟合中，采用了带相位的周期函数，使用该函数拟合出的初相并不稳定，可能在制作网格以及使用网格的插值过程中引入误差。

为了填补这些内容的空缺，本文提出了一套ZTD建模质量控制方法，采用内华达大地测量实验室(Nevada Geodetic Laboratory，NGL)解算的高空间分辨率GNSS对流层数据，选取了近10年德国及周边区域[47°N-55°N，5°E-15°E]183个测站的实测ZTD，对该方法进行了检验。该方法从建模数据量的选择、网格分辨率对模型精度的影响和模型产品稳定度等方面对模型进行了质量控制。同时，本文提出了无相位周期拟合模型并对比分析了其相对于文献[4]中含相位模型的优势。最后，本文建立了在该质量控制方法和新拟合方法下所选区域的ZTD模型。新模型稳定可靠，精度优良，检验了该质量控制方法的可行性。

1 数据处理策略与模型质量控制

1.1 建模步骤

相比于传统模型，基于GNSS观测数据的ZTD模型与气象参数无关，其建模数据来源于区域或全球分布的GNSS永久观测站的实测ZTD，模型建立过程中充分考虑ZTD的时空分布特性，能够最大程度地保证模型在GNSS应用中的自洽。文中，为了使得模型网格尽可能的平滑以降低插值带来的误差，在数据处理策略上，首先剥离高程给ZTD带来的影响，即将测站ZTD归化到椭球面上，然后再网格化。

本文的建模步骤为：1)获取区域的GNSS测站坐标信息以及长时间的ZTD数据；2)分析测站高程与ZTD年均值的关系，采用指数模型计算ZTD随高程的衰减系数，根据计算获取的系数将ZTD归化到椭球面上；3)采用频谱分析方法提取测站ZTD时间序列里的周期信号，使用周期函数对时间序列进行拟合，获取各个测站的拟合参数；4)分析各个参数水平方向的分布特点，对各个测站的拟合参数采用双线性插值方法在经纬度上进行网格化，获取各网格点的参数，制作成网格文件。

模型的使用过程与建立过程互为逆过程，其步骤为：1)获取网格文件，通过搜索和用户最近的4个网格点，使用双线性插值方法获取用户所在经纬度的周期函数拟合参数；2)将参数带入周期拟合模型，获取给定年积日下用户所在经纬度椭球面上的ZTD；3)使用指数模型，带入衰减系数参数，将椭球面上的ZTD改正到用户所在高程，求得测站的ZTD。

建模及使用具体流程如图1所示，图1上部点划线框中为模型建模过程，下部点划线框中为模型的使用过程。对于用户而言，仅需提供测站坐标和年积日，代入模型，便能获取实时ZTD。

1.2 数据质量评估

高空间分辨率以及高精度的实测GNSS ZTD是模型建立的基础。2017年11月5日，NGL的Geoff Blewitt等人开放提供了自1996年以来全球超过1.6万个站点超过3400万天次的对流层产品[23]，每年新增测站数量约为1000个。NGL提供的对流层产品使用了JPL/Caltech提供的轨道和钟差，使用GIPSY软件进行解算，时间分辨率为5 min，产品遵循IGS标准格式。相比于IGS对流层产品，NGL对流层产品测站分布范围更广，分布密度更大，可用时间更长。NGL对流层数据的开放对于对流层延迟的精细建模研究具有重要的意义。

相比于全球模型，区域模型由于空间跨度较小，建模更加精细，往往能够获得更高的精度。鉴于德国区域NGL测站数量多且分布均匀，且该区域是用于建立欧洲气象基础模型的主要观测区域之一，为便于与GPT2w等基于NWM再分析产品的模型进行对比分析，本文选取了2009年1月1日至2018年12月31日期间德国及周边区域[47°N-55°N，5°E-15°E]217个测站的ZTD数据，用于实验分析。

NGL并未公布其对流层产品的精度，为了评估本文使用的NGL对流层产品的精度，以下以IGS ZTD为参考，统计了10年期间所选测区的10个共有测站的NGL ZTD的平均偏差(BIAS)和均方根误差(RMS)。统计方法见式(1)，统计结果见表1，从表1可以看出，测区内的NGL ZTD和IGS ZTD一致性良好，10个测站BIAS均值为0.87 mm，RMS均值为3.88 mm。该结果表明NGL解算的ZTD具有和IGS解算的ZTD相同的精度，可用于对流层延迟精细建模。(IGS提供的最终ZTD产品精度为4 mm；http://www.igs.org/products，2019.7)

(1)

式中：B为BIAS，R为RMS，ZIGS为IGS ZTD序列，ZNGL为NGL ZTD序列，N为序列长度。

1.3 数据量对模型的影响

图2中柱状图为所选测区内各个测站数据可用时间的频数分布直方图，从图中可知各个测站之间可用数据差异较大。前人的研究中[4,21]，仅简单剔除了数据量偏少的测站，未在数据量的选择对建模精度的影响上进行深入研究。为了解决不同数据量的测站用来一起建模是否合理、数据量越多是否越有益于提高模型精度等质量控制问题，实验选取了数据量满10年的15个测站，计算了分别使用1年至10年数据量建模，测站的平均拟合RMS值，结果如图2所示。可以发现，随着数据量的增多，RMS值在增大，幅度约为0.8 mm/年，但在数据量超过4年后，RMS逐渐平缓。由此可以得到结论：1)ZTD在年与年之间存在差异，这种差异在数据量超过1年的情况下会使得RMS值变大；2)这种差异的周期约为4年，在数据量超过4年后，RMS值趋于平缓，因此在数据量的选取上，建议不超过4年；3)这种差异的幅度为毫米级，将不同数据量的测站一起建模对精度影响有限。在本文中，考虑到在时间序列拟合过程中使用了年周期拟合模型，实验对217个测站进行筛选，在剔除数据量不足1年的测站后，选取了2015-2018共4年期间183个测站的ZTD数据进行建模。

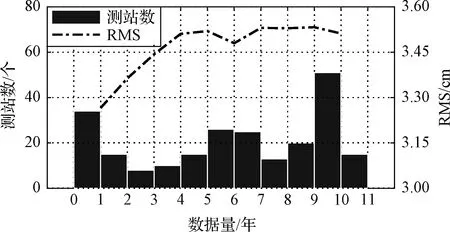
图2 数据可用时间频数分布和建模数据量 与模型RMS之间的关系Fig.2 Data available time frequency distribution & Relationship between modeling data volume and model RMS

表1 NGL解算的德国区域IGS测站ZTD精度Table 1 ZTD accuracy of the IGS station in The German region calculated by NGL (mm)

1.4 网格分辨率对精度的影响

测站空间分辨率的大小直接决定了模型的精细程度，而网格分辨率的选择与测站空间分辨率相关。前人的研究[4]中未阐明其网格分辨率的选择依据，无法获知网格分辨率对模型精度的影响。为了探究网格分辨率对模型的影响，以确定合适的网格分辨率，本文统计了在使用相同的数据、相同的建模方式下划分成不同大小网格下的模型精度(BIAS和RMS)以及模型使用的成本(网格文件大小及计算耗时)。实验结果如表2所示，由于网格数量与网格点分布相关，难以统计，本文中以网格点数量代替，表中平均测站数为测区内用以建模的测站个数与网格点个数之商。从表2可以发现：1)随着网格密度的增大，网格点数量、网格文件大小呈指数增长，计算耗时前期增长不大，后期增长迅速；2)RMS随着网格的变小逐渐变小，当分辨率小于1°×1°后，RMS趋于稳定，BIAS随着网格的变小有明显的下降；3)网格分辨率在小于1°×1°之后，网格平均测站数小于1。综合考虑，1°×1°的网格分辨率在本文中为最佳网格划分标准，在该标准下，既保证了高精度(BIAS小于1 mm)和高效率(耗时较低)，又能保证了低成本(网格文件占用内存较小)。从以上结果可以得到网格分辨率选取的一般标准：在保证平均每个网格内至少1个测站的前提下选择大网格。在该标准下，能够在充分发挥测站分辨率大的优势同时控制建模及使用成本。

1.5 模型稳定性

由1.3节可知，建模数据时长的增加并不能有效地提高模型精度，可见ZTD具有较高的稳定性。为了检验该结论并探究模型精度在模型使用过程中随时间的变化，实验选取了数据量满10年的15个测站2009-2012年共4年的数据进行建模，然后对2013-2018共6年时间的ZTD进行预报。图3为15个测站的预报残差平均值的时间序列，图中点划线为残差序列的线性拟合，可以发现，在长时间的预报过程中残差序列存在逐渐变大的趋势，残差序列变化率为1.42 mm/年。考虑到模型精度为厘米级，该趋势变化并不大，模型精度整体相对稳定，无需频繁(每年)更新，该模型可以在建模后的较长一段时间以其标称精度提供服务。

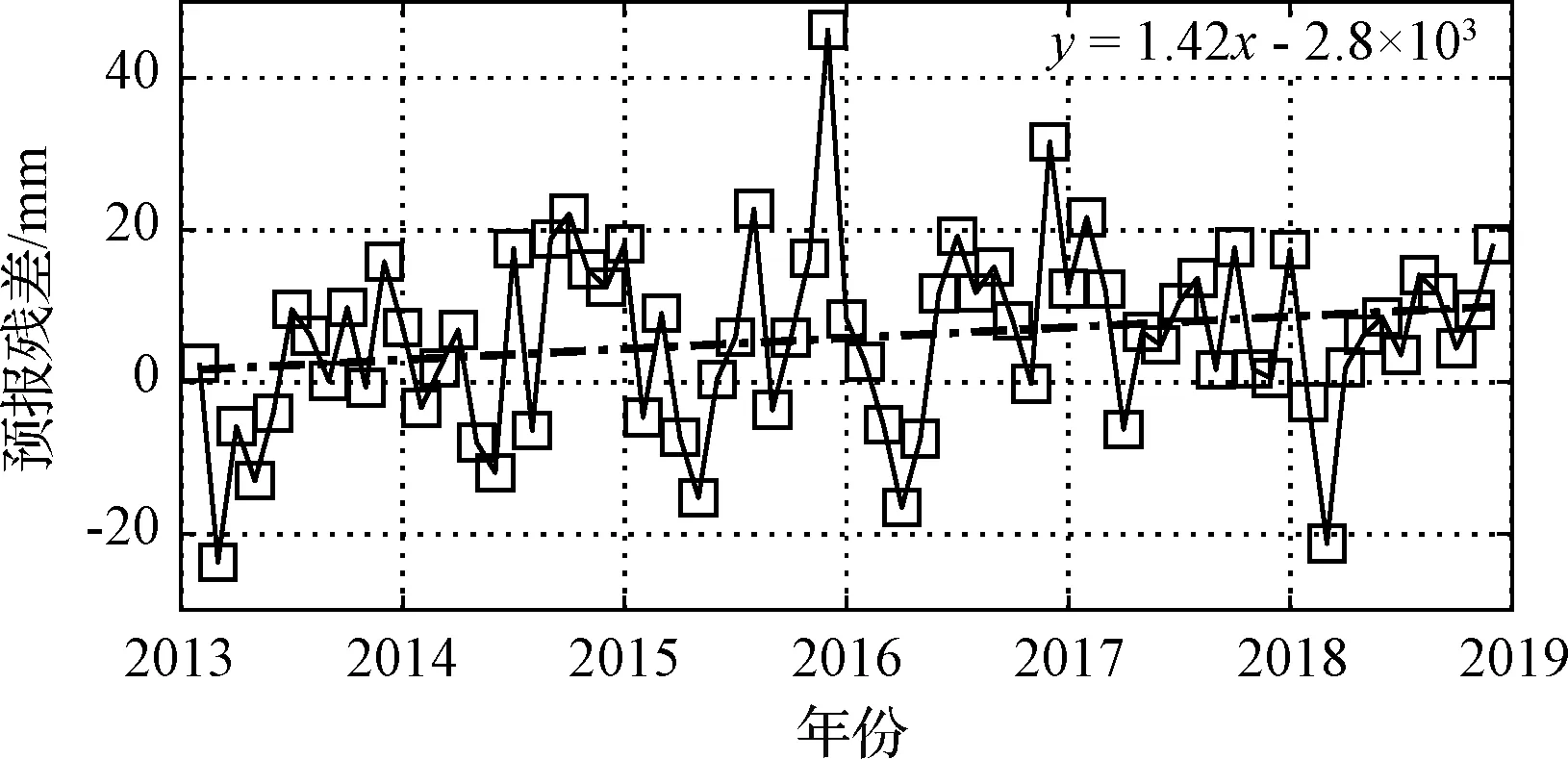
图3 模型预报残差Fig.3 Model prediction residual

2 结果与讨论

为了检验上述质量控制方法下的模型精度，本文对在该区域选取的183个测站数据，进行了ZTD时空特性分析，建立了相应的ZTD模型，该模型以下称为SHAtropDE(DE为德国的简称)。

2.1 高程归化

图4为各测站高程以及各测站的ZTD均值，本文中的测站高程均为基于椭球面的大地高。从图中可以发现，德国地势整体较为平缓，南部由于靠近阿尔卑斯山脉高程出现陡增，而ZTD年均值正好相反，在南部出现陡降，测站高程与ZTD近似呈反比关系，即测站ZTD年均值随着测站高程增加减小。ZTD与测站高程的关系通常用指数模型或者线性模型来表示[22]，以下为指数模型关系式：

Z(h)=Z0×exp(βh)

(2)

式中：Z(h)为测站所在高程ZTD，Z0为测站在椭球面上的ZTD，h为测站高程(m)，β为ZTD随高程的衰减系数。

实验通过对测站4年的ZTD年均值与测站高程进行指数模型拟合，得衰减系数β=-1.24×10-4。获取衰减系数后，即可将ZTD归化到椭球面上。

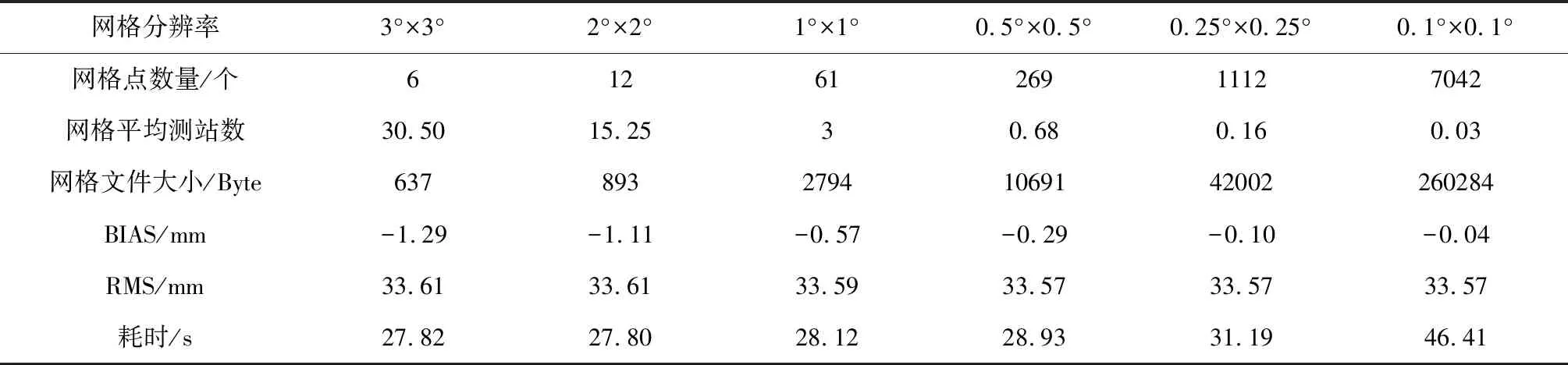
表2 不同网格分辨率下模型精度及使用成本Table 2 Model accuracy and cost of use at different grid resolutions

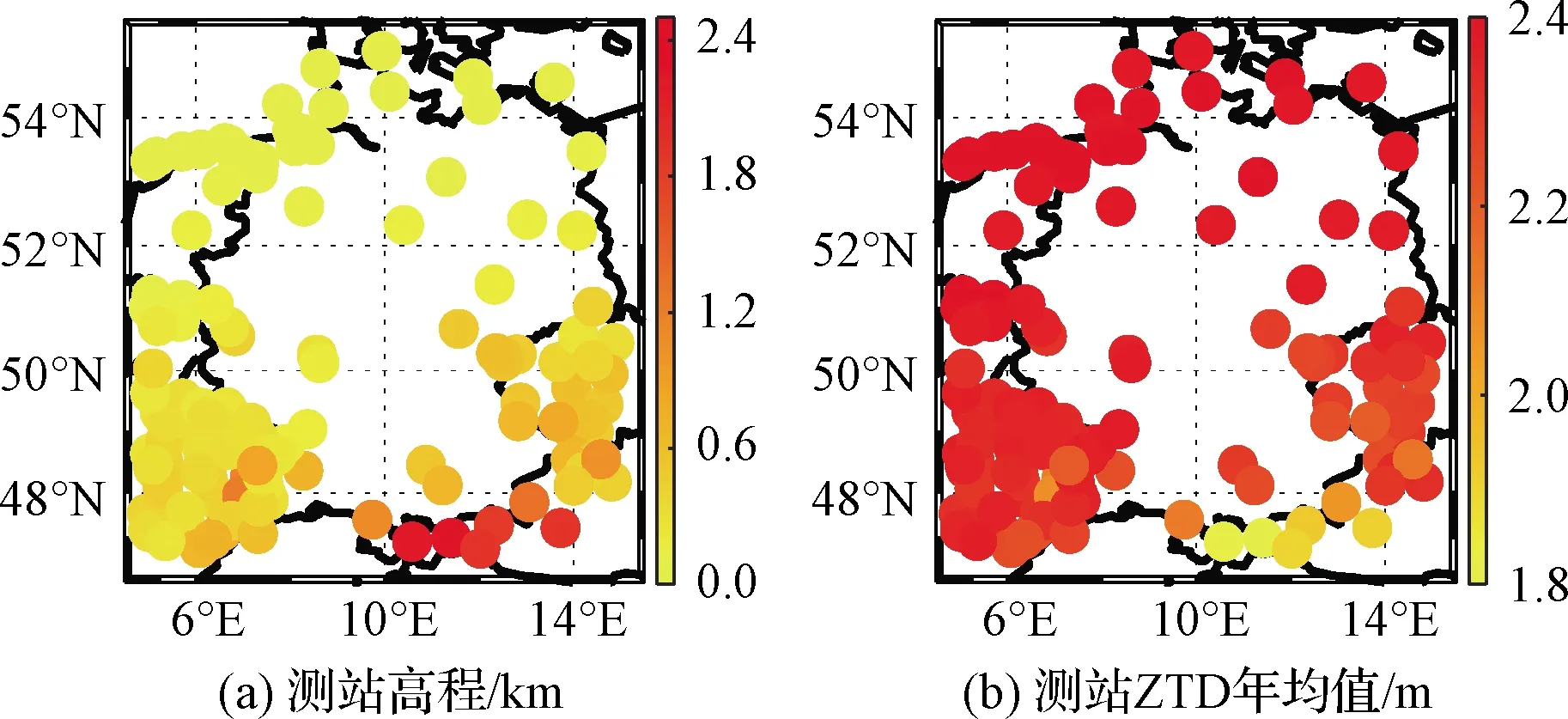
图4 测站高程和测站ZTD年均值Fig.4 Station elevation and station ZTD annual mean

2.2 时间序列周期拟合

由2.1节可知测站ZTD与测站高程相关，而对于单个测站而言，其高程固定，ZTD随时间的变化规律与高程无关。图5为PTBB测站的时间序列，可以发现ZTD时间序列存在明显的周期信号。时间序列的周期信号通常通过傅里叶频谱分析[24]来获取，实验对全部测站数据做傅里叶频谱分析后发现全部测站均存在显著的年周期信号。

在处理ZTD随时间的变化中，文献[4]采用了年周期+半年周期拟合模型，公式见式(3)。该模型含有相位参数，为了克服由该相位参数带来的模型误差，本文提出使用无相位拟合模型。为了判断在本实验所在区域中，年周期+半年周期是否同样优于仅年周期模型，本文提出了两种无相位模型，第一种为无相位仅年周期模型，见式(4)；第二种为无相位年周期+半年周期模型，见式(5)。

(3)

(4)

(5)

式中：A,A1,B1为年周期项振幅，B,A2,B2为半年周期项振幅，P1,P2分别为年周期和半年周期项相位，C为常数项，τ为年积日。

实验对式(4)和式(5)模型、式(3)和式(5)模型下的RMS进行了对比实验。实验结果如图6所示。图中分别以“H”“N”“O”代表无相位仅年周期模型、无相位年周期+半年周期模型和含相位年周期+半年周期模型。

从图6 (a)子图可以发现，无相位仅年周期模型和无相位年周期+半年周期模型RMS序列接近，但RMS差值序列全部为正，说明在本实验所在区域内所有测站在附加半年周期模型下精度高于仅年周期模型。根据图6 (b)子图，使用无相位模型精度高于含相位模型，证明了新模型的优越性。PTBB站使用式(5)模型的拟合结果以及拟合残差也绘制在图5中，图中对残差取了绝对值，从图5可以发现，拟合残差基本控制在±10 cm以内，且残差序列呈现噪声特性，不存在残余的周期信号，拟合情况良好。

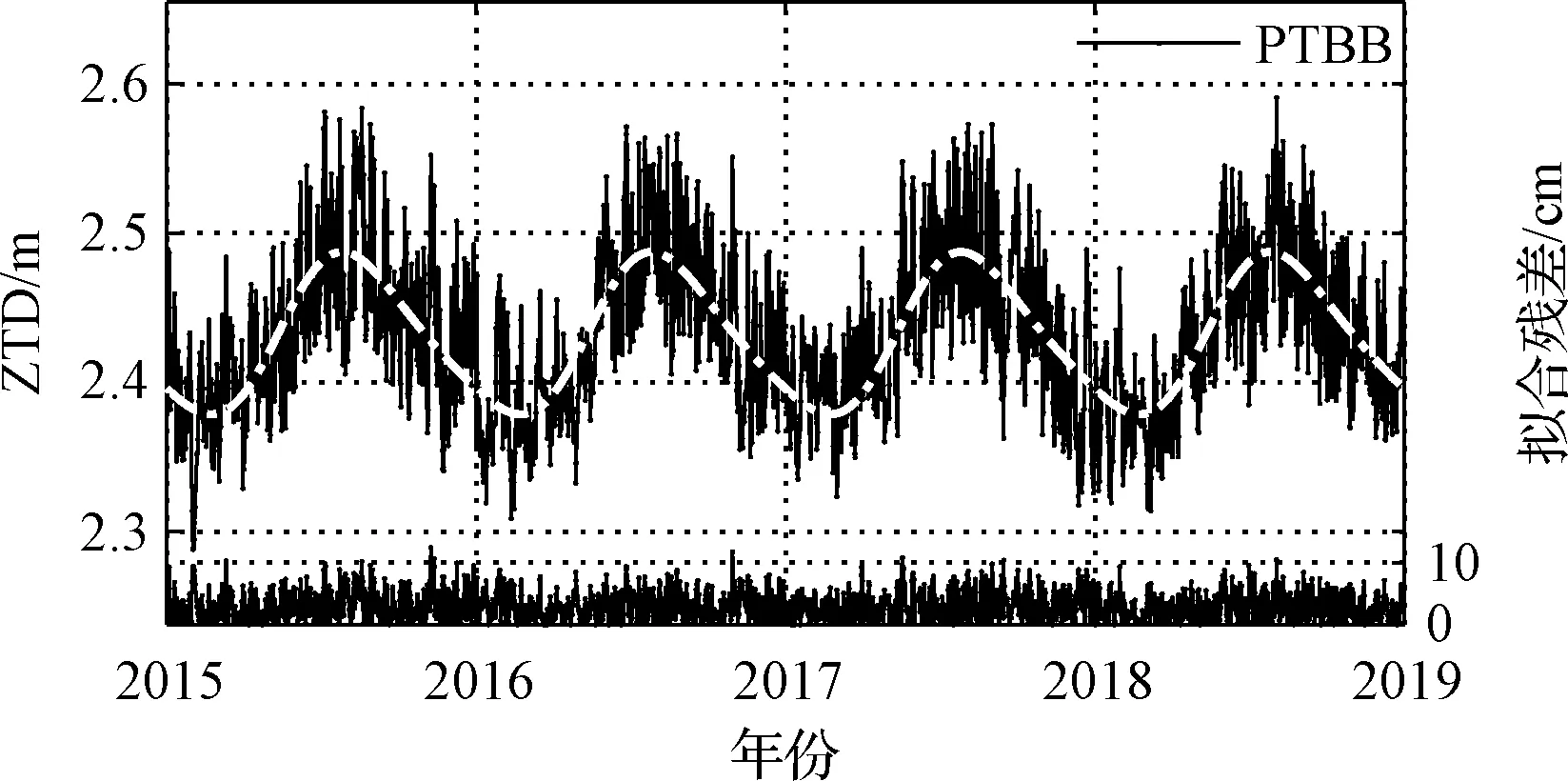
图5 测站ZTD时间序列与周期函数拟合结果及拟合残差Fig.5 Station ZTD time series and cycle function fit results and fitting residuals

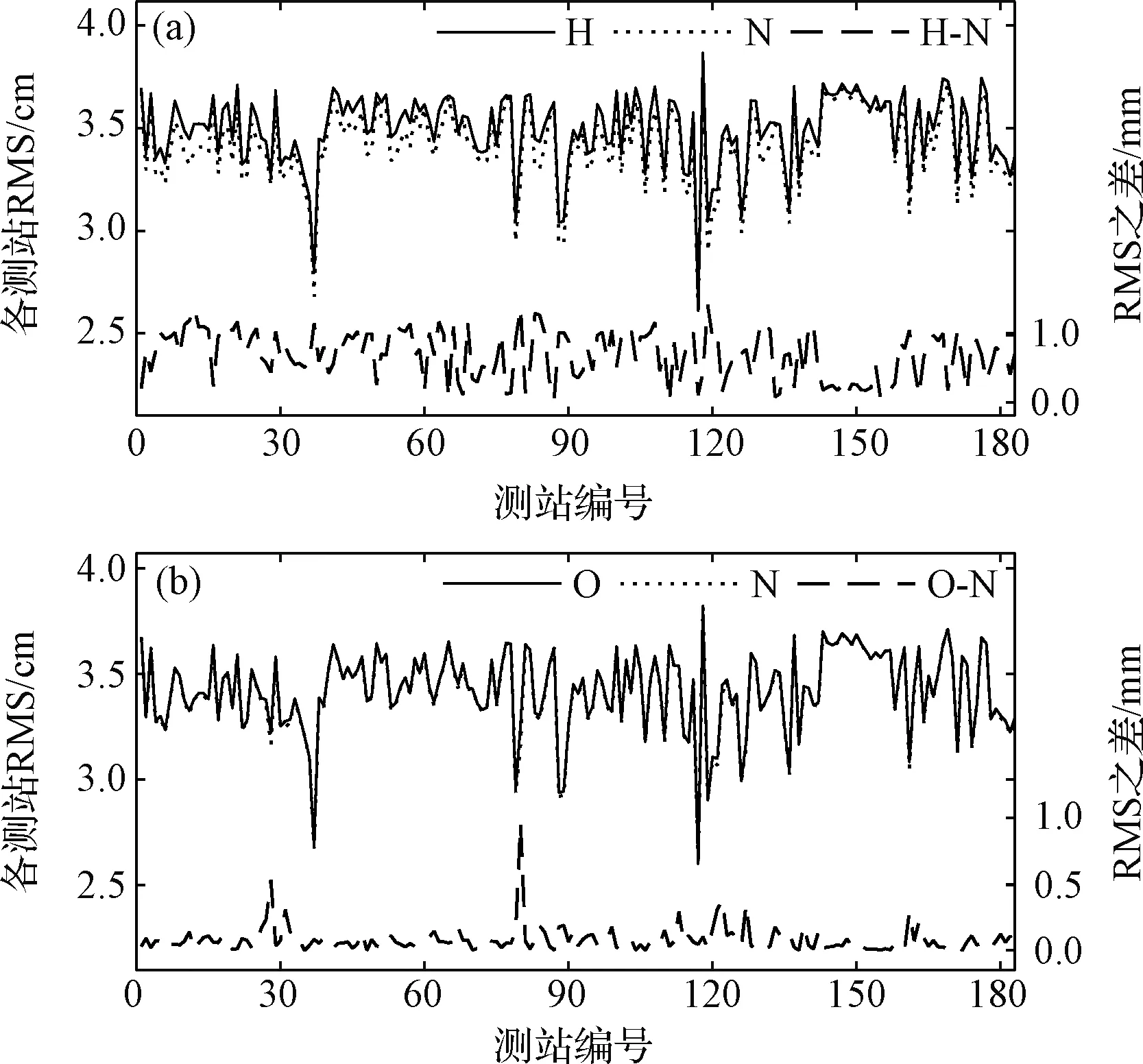
图6 三种拟合模型下各个测站RMS比较Fig.6 RMS comparison of each station under three models

2.3 水平方向网格化

实验选取183个测站中的170个用于建模，剩余的13个用于检验。图7为建模站做年周期+半年周期拟合的5个拟合函数参数和拟合残差的中误差。从图中可以发现：年周期项振幅A1表现为西北部大、东南部小，并有向东南方向层进减小的趋势，而B1无显著地域特性；半年项振幅A2可以看出存在南大北小的地域分布，而B2同样无明显地域特征；常数项C在西南区域较大，在南边界靠近阿尔卑斯山处较小，其余区域呈现由北向南增大的特点；拟合残差中误差RMS呈现从临海的西北区域向靠近阿尔卑斯山脉的东南内陆逐渐减小的特点，可见水汽活跃程度极大影响拟合精度。测站中拟合残差中误差最大为3.71 cm(VLIE∶5.09E, 53.30 N)，最小为2.90 cm(PAT2∶11.46E, 47.21 N)。

2.4 模型精度评估

为了评估SHAtropDE的精度，本文利用SHAtropDE计算了所选测区内183个测站2015-2018共4年的ZTD，同时计算了EGNOS、UNB3m和GPT2w模型在相同测站、相同时间段的ZTD，并以NGL解算的ZTD作为参考值，计算了各个模型的BIAS和RMS，计算公式见式(1)。各模型下各个测站的BIAS如图8(a)至(d)，RMS如图8(e)至(h)。

从BIAS和RMS可以看出，UNB3m模型整体精度最低，EGNOS和GPT2w精度相当，SHAtropDE模型精度最高。EGNOS和GPT2w的BIAS以及SHAtropDE的RMS均呈现南高北低的地域特性，SHAtropDE模型BIAS最小且分布均匀。

表3统计了170个建模站和13个检验站在四个模型下的BIAS和RMS信息(平均值，最小值，最大值)，从表3可以得到以下结论：SHAtropDE模型在建模站和验证站精度相当，平均BIAS小于1 mm，平均RMS为3.4 cm；SHAtropDE模型的整体精度最高，建模站相对于UNB3m、EGNOS、GPT2w+Saas平均改善了42.4%、35.8%、33.3%；验证站相对于UNB3m、EGNOS、GPT2w+Saas平均改善了30.8%、40.7%、38.6%。SHAtropDE模型基于实测ZTD建立，相对于传统经验模型有良好的精度改善，能够满足德国区域GNSS用户高精度ZTD改正需求。

3 结 论

本文提出了一套ZTD建模质量控制方法，并采用NGL解算的高空间分辨率GNSS对流层数据，选取了近10年德国及周边区域[47°N-55°N，5°E-15°E]183个测站的实测ZTD，对该方法进行了验证，得出了以下结论：

1)ZTD在年与年之间存在大小约为0.8 mm/年的拟合差异，这种差异的周期约为4年，使用超过4年的数据对模型精度提升作用不明显；

2)网格分辨率的选取应以保证平均每个网格内至少一个测站为标准。在该标准下，能够充分发挥测站分辨率大优势并控制建模及使用成本；

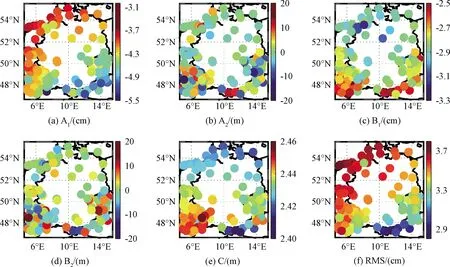
图7 各测站拟合残差及拟合参数Fig.7 Fitting residuals and fitting parameters of each station

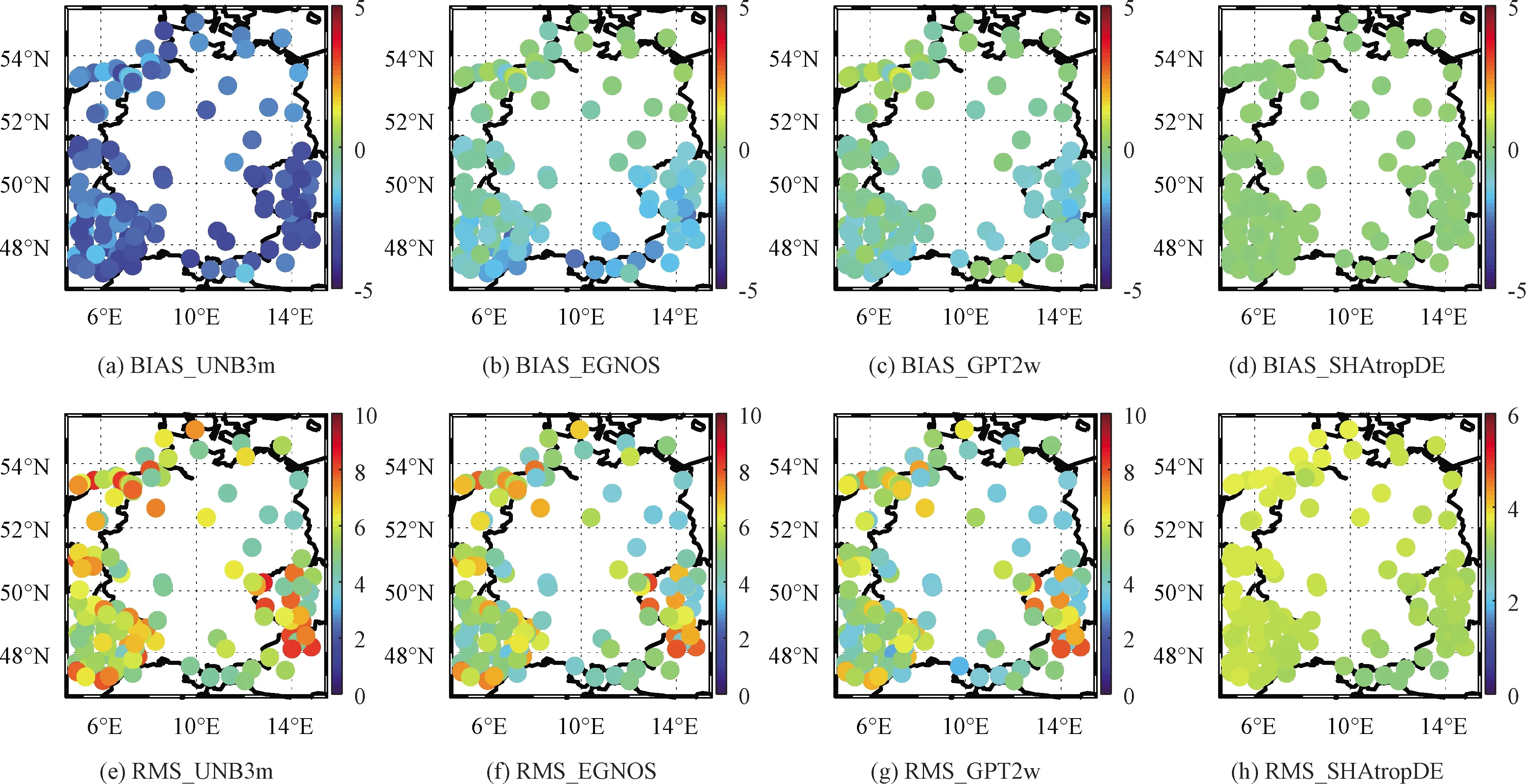
图8 各测站不同ZTD模型的系统偏差(cm)和RMS精度统计(cm)Fig.8 System deviation (cm) and RMS accuracy statistics (cm) for different ZTD models at each station

表3 SHAtropDE模型的精度与其他模型的对比Table 3 Comparison of the accuracy of the SHAtropDE model with other models (cm)

3)模型在长时间的使用过程中存在精度略微退化的现象，残差序列变化率为1.42 mm/年。模型精度整体相对稳定，无需频繁(每年)更新，可以在建模后的较长一段时间以其标称精度提供服务。

在本文质量控制方法下建立的新模型平均RMS为3.4 cm，相对于UNB3m、EGNOS、GPT2w+Saas平均改善了42.4%、35.8%、33.3%，能够满足德国区域GNSS用户高精度实时ZTD改正需求。该方法为此类ZTD模型的建立制定了技术规范，能够给其他区域的建立类似模型提供良好的参考作用，对于ZTD建模研究具有一定的参考价值。