高中数学解析几何问题的解题技巧

徐海棠

(江苏省盐城市第一中学 224000)

一直以来，解析几何问题都是高中数学考试中的重点考查内容，相较于代数问题，其具有更强的抽象性，很多同学在解答立体几何问题时不能够准确把握题目内容与基础条件，不能够灵活选择相对应的解题方法与解题技巧.因此，下文主要是结合常见的集中立体几何问题类型，提出相对应的解决方法，讲解一些解题技巧，以供参考.

一、中点弦问题——几何与代数相结合

“中点弦问题”是高中解析几何问题体系中较为常见的类型，也是各学期、年段的期中考试、模拟考试与高考中最容易出现的问题形式之一，结合以往的解题经验可以发现，在解析几何中点弦问题中，使用坐标系，实现数形转化是一种较为常用的解题技巧.很多时候，同学们在缺乏思路，不能够很好地解题的时候，使用数形结合的方法往往能够在较短的时间内找到解题的“切入点”.在解题过程中，可以分别把握几何中作为一般轨迹的圆、圆锥曲线，结合坐标系，探索曲线的对应方程，以此掌握这些方程下的几何性质.

例1 已知A、B是抛物线y2=4x上的两点，弦AB的中点是M(2，1)，求弦AB所在直线l的方程.

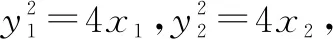
所以直线l的方程是y-1=2(x-2)，即2x-y-3=0.

此外，关于“中点弦问题”，还可以使用其他的解题方法，具体还要结合题目中的基础条件，以此提高解题正确率与解题效率.

二、轨迹方程问题——直接法

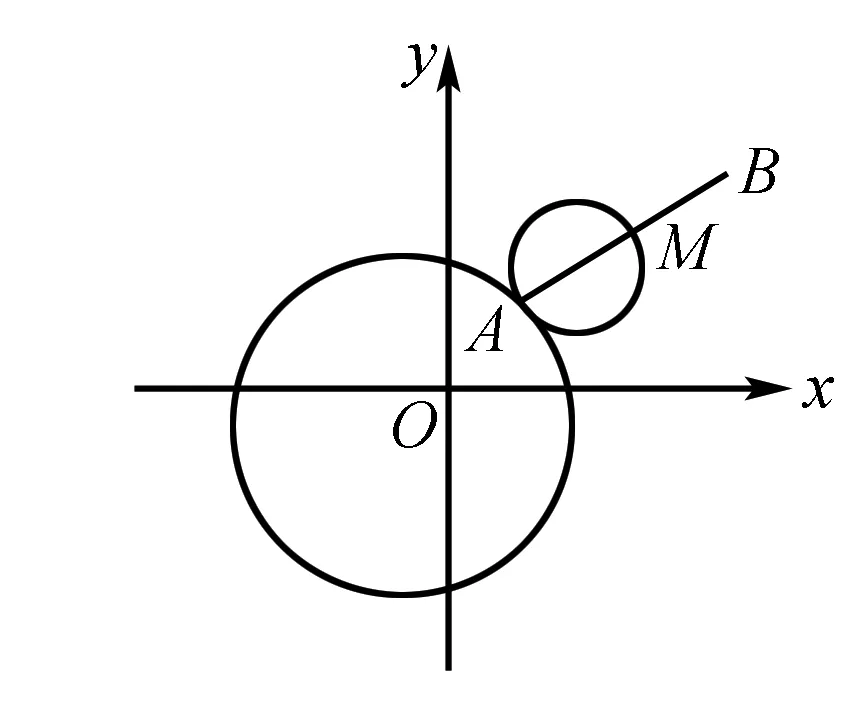
图1

轨迹方程问题，就是与几何轨迹对应的代数问题.一般情况下，能够满足一定条件的动点所形成的图形的问题可以称之为“轨迹方程问题”,或者是符合基础条件的点的全体所组成集合相关问题，可以看做是“轨迹方程问题”.轨迹，可以从两方面进行分析，一方面是在轨迹上的点都符合基础条件，为轨迹的必要性；另一方面，是不在轨迹上的点都不符合已经设定的基础条件，这叫做轨迹的充分性.在高中解析几何问题的解题过程中，可以发现空间轨迹一般都是“曲面”，而平面轨迹一般都是曲线(如图1).

关于轨迹方程，同学们可以通过“直接法”进行求解.所谓“直接法”就是在假设动点的运动条件符合几何的等量关系的基础条件下，同时基础条件明确，不需要特殊的解题技巧，可以将几何关系通过“x与y”体现出来直接得到轨迹方程.

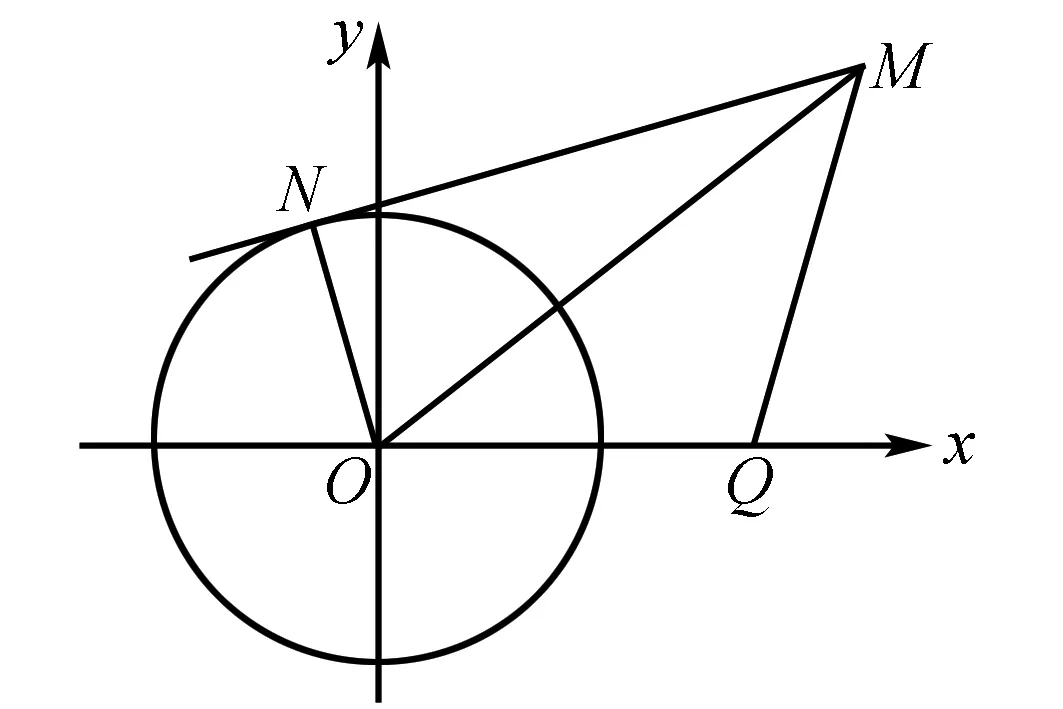
图2

在使用直接法时，要遵循以下思路，分别为：①建立坐标系；②设轨迹上的点P(x，y)；③列出动点P的相关关系式；④结合条件选用相应公式(斜率公式、距离公式)列出方程；⑤证明所求方程就是符合条件的P的轨迹方程.

例2 在平面直角坐标系中，已知点Q(2，0)，圆C：x2+y2=1，动点M到圆C的切线长度与|MQ|之比等于常数λ，且λ>0.求：动点M的轨迹方程，动点M的轨迹方程是什么曲线？

此时，就可以使用上述提到的“直接法”进行解题.

三、曲线问题——定义法解题

相较于上述的“中点弦问题”与“轨迹方程问题”，还存在一些几何问题，这些几何问题的基础条件更加复杂，可以统称为“曲线问题”，比如：抛物线问题、双曲线问题、椭圆问题等.定义解题法主要就是在已经分析或者说明动点P的轨迹确实符合某种特殊曲线基本特征之后，求出特殊曲线的相关参量数值，最终得到轨迹方程.

例3 已知两点A(-8,0)、B(8,0)为△ABC的两个顶点，AC与BC两边的中线长的和为30，求△ABC的重心轨迹方程.

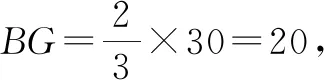
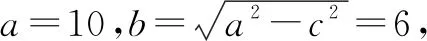
总之，解析几何问题难度较大，且题型复杂多变，在解题的过程中往往需要运用到大量的基础知识，比如：函数相关知识、坐标相关知识、向量知识等，还需要能够结合不同类型的解析几何问题，选择合适的解题方法，比如：数形结合、直接法、定义法、减少计算量”原则等，从而提高解析几何的解题效率，帮助同学们掌握解析几何解题技巧.