领会考点 研究题型 提升学生的解题能力——以苏科版教材“平面解析几何”为例

徐 崇

(江苏省常熟市梅李高级中学 215500)

高中数学教学面临的一个根本任务，就是在立德树人和核心素养培育的背景之下，培养学生的解题能力.这样的教学定位，意味着要将立德树人与核心素养培育，与很现实的培养学生的解题与应试能力结合在一起.而这也就意味着在日常的教学中，教师要重视学生的数学知识及其体系的建构，同时又要在此基础上切实培养学生的解题能力.面对这一任务，有研究者明确指出高中数学教师要基于新时代高考的核心功能和主要任务，进而领会《普通高中数学课程标准(2017年版)》《2018年普通高等学校招生全国统一考试大纲(理科数学)》的精神，研究普通高等学校招生全国统一考试数学卷中试题与服务选才这“一把尺”之间的关系，从高考解析几何试题中分析考查题型、内容、热点等角度展开研究，从而寻找到关于高考数学知识的基本考向以及备考思路.本文试以苏科版教材“平面解析几何”为例，谈谈笔者的探究过程与结果，以期对同行的相关研究起到抛砖引玉的作用.

一、领会考点，奠定解题能力提升的基础

平面解析几何是高中数学知识体系中的基础性知识，同时也是高考的必考内容，平面解析几何的基本思想实际上是用代数方法解决几何问题.从当前高考实际情况来看，几何性质考查内容主要以离心率为主，而相应的学生学习的难点主要与取值范围、最值等问题相关.也正因为这个原因，圆锥曲线的离心率、取值范围和最值问题成为平面解析几何知识考查的重要指向.这实际上是从考点的角度，对平面解析几何知识进行的研究，而要培养学生的解题能力，首先就必须以考点知识的领会来奠定解题能力培养的基础.

从宏观角度来看，平面解析几何部分的知识涉及到的考点虽然很多，但与圆锥曲线相关的考点，由于其具有综合性，以及利用圆锥曲线相关知识解决问题时能够涉及比较广泛的知识，因而既表现出一定的解题难度，又表现出相应的解题能力培养的空间.

当然作为对考点的研究，面向培养学生解题能力的需要，还必须研究更加细致的“点”.比如说，椭圆中的最值问题包括两种：一种是参数的取值范围问题，另一种是长度与面积的最值问题.最值问题一般都与动态变化相关，因此在解题的时候要引导学生认识到，前者往往需要根据图形的几何特征去建立起与某个参数相关的不等式或者函数，而后者则主要是通过建立关于某个参数的函数，然后运用基本不等式或函数知识去求解的.当然最终能力的形成，在于学生具体的练习过程，而这就涉及到题型研究.

二、研究题型，铺就解题能力提升的大道

通常情况下教师对题型研究往往进行得比较深，比较透，但笔者在教学中发现，要想有效地培养学生的解题能力，还必须带着学生去研究题型，要让学生对题型有非常感性的认识，这样他们在解题的时候才能做到心里有数.如果把解题和考试比作打仗，那对题型的研究实际上就是为了做到知己知彼而百战不殆.

例如有这样一道题目：已知点A(-2，0)、B(2，0)，动点M(x，y)满足直线AM与BM的斜率乘积为-1/2.记M轨迹为曲线C.(1)求C的方程，并说明C是什么曲线；(2)过坐标原点的直线交C于P、Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE并延长交C于点G.(ⅰ)证明:△PQG是直角三角形;(ⅱ)求△PQG面积的最大值.

虽然这是全国卷上的题目(2019年高考全国Ⅱ卷理科第21题)，但是笔者认为其对江苏的考生也有一定的指导作用.这道试题考查了曲线的方程、直线和椭圆的位置以及最值问题，考查的是学生分析问题与解决问题的能力.在问题解决的过程中，涉及到逻辑推理、直观想象、数学运算等数学核心素养；从实际解题的角度来看，试题解法灵活，内涵丰富，综合性强，为不同学生搭建了施展才能的舞台，是一道好题.认为它是好题，还有一个重要的原因，这就是这是一种有代表性的题型，这一题型所涵盖到的平面解析几何知识，以及涉及到的解题能力，都能够让学生在解题的过程中，获得知识的巩固与能力的提升.

比如说，在具体的解题过程中，可以让学生遵循一题多解的思路，将题目中给出的信息与问题，与原有的解题经验结合起来，以从多个角度寻找问题解决的方法.笔者在课堂上引导学生解题的时候，选择了这样几个角度(限于篇幅，这里以第2问为例)：

角度1：让学生先设出直线PQ的斜率为k，然后得出直线的方程，也就是y=kx(k>0)，然后与此前得到的C的方程联立，就可以求出x(用k来表示)；其后经过几次代换之后，则可以得到一个以k为系数的方程，即(2+k2)x2-2uk2x+u2k2-8=0；再然后就可以借助于韦达定理与斜率的知识求解.这个过程中，多次化简与消元，并借助于函数的单调性求出了△PQG面积的最大值.此过程中学生的思维量极大，多次转换才能实现难点的突破，这实际上就赋予了学生一个充足的培养自身解题能力的空间.

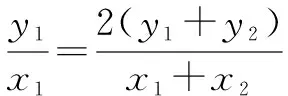
这是两个不同的解决问题的角度，尽管在课堂上花费一定的时间，但是无论是涉及到的数学解题方法，还是运用到的数学知识，都能够有效地帮学生拓宽眼界，提升学生的解题层次，从而提升学生的解题能力.

三、因材施教，落实解题能力提升的要求

在实际教学中笔者发现，由于学生之间的个体差异，同样一个考点的确定与相应的题型的选择，不同学生在训练的过程中，表现出来的接受能力以及解题能力的提升幅度是有所差异的.从这个角度来看，高中数学教师要想切实提升学生的解题能力，就必须做到以生为本而因材施教.

如同上面所强调的一样，平面解析几何一直是高中数学的重要内容之一，在历年的高考中也都是考查的重点，因此这是我们高考复习的重头戏.从近几年江苏高考的情况来看，涉及到平面解析几何的题目还是比较丰富的，本质上这是因为平面解析几何知识内容较多，方法性、思想性都很强，因此高中数学教师要在高三复习中提升复习效率，就必须有策略地部署复习安排.笔者在教学中，关于这一知识所进行的复习部署中，很重要的一点就是先去研究学生个体.当然由于班级授课制的关系，再加上所教班级不止一个，因此也不可能真正地面向每一个个体进行研究.但是将学生分成不同的层次，研究每一个层次学生在平面解析几何知识的学习中，所表现出来的知识理解能力、思维能力等，然后去实施教学，就可以取得比较好的效果.

总的来说，面向学生解题能力的提升需要，并在此基础上满足学生数学学科核心素养培育的需要，数学教师就必须认真研究考点，准确把握题型，然后再面向不同层次的学生，施以不同的解题教学策略，这样就可以切实提高学生的解题能力.而且事实表明，这样的教学思路是能够满足绝大多数学生的需要的，学生对这样的教学方式也是比较欢迎的，从教学效果的角度来看，坚持使用这样的教学思路，学生的解题能力可以得到明显提升，而数学学科核心素养也能够在这样的过程中得到培养.