引入微课故事 渗透数学思想——《集合》教学

夏燕萍

【教学内容】

人教版三年级上册第104、105 页。

【教学过程】

一、设疑引入，激发兴趣

1.谈话设疑。

师：学校在元旦之前举行了迎新文艺汇演，我们班有两个节目参加。

（媒体出示：参加唱歌的有4人，参加跳舞的有5 人）

师：猜猜看夏老师一共推荐了几人参加？

生：9 人。（板书9）

师：有不同想法吗？

生：8 人。（板书8）

师：到底是几人呢？

2.出示名单，引出重复。

师：唱歌队有杨明、陈东、李芳、王爱华，这4 个人形成了唱歌队的集合；跳舞队有陶伟、王爱华、于丽、陈东、丁旭，这5 个人形成了跳舞队的集合。

师：现在把这些同学全部框起来，这就是我们班所有参加迎新活动同学的集合。你从中发现了什么？

生：陈东和王爱华两个节目都参加了。

生：一共只有7 个学生。

师：陈东和王爱华既唱歌又跳舞，两人的名字重复出现。（板书：重复）

【设计意图：从参加唱歌、跳舞的人员统计入手，将其改编成了人数分别只有4 人和5 人同样类型的问题，发现重复现象，引出集合问题，从生活的实际出发，去发现问题、解决问题，从而收获新的知识。根据对于同一个问题产生的不同答案引发了“冲突”，激发学生自主探究的欲望，让学生积极主动地投入解决“一共推荐了几人”这一问题的活动中去，用个性化的思考和处理问题的方式解决问题，为他们自主构建知识的意义提供时空保障。】

二、问题引领，建构模型

1.明确要求，探索方法。

师：为了清楚地表示出我们班一共有多少人参加了表演，老师为大家提供了一张《学习单》。你能不能借助图、表或其他方式，让其他人能清楚地看出我们班参加人员的信息呢？请在《学习单》上把你的想法记录下来。

2.展示交流。

师：咱们班同学的想法很有创意，我从中选了几份，这些作品，你喜欢哪一个，为什么？

生：我喜欢用文字的方法来表示，很清楚。

生：我喜欢用连线的办法把重复出现的名字连起来。

生：我喜欢直接在表格上把重复出现的名字圈起来。

生：我喜欢用画圆圈的方式，这样一目了然，在科学书上我也看到过。

师：像刚才我们同学所表示的，有用文字表示集合的、有用符号表示集合的、还有用画图的，它们都有一个共同点，都用不同的方式表示了唱歌同学的集合和跳舞同学的集合。

师：谁听过集合？

生：体育课上老师会说集合。

师：在数学中，到底什么是集合呢？这就是我们今天要来研究的内容。（板书：集合）

用微视频的方式播放《集合的故事》：集合是什么呢？参加唱歌的同学就是一个集合，每位参加唱歌的同学就是这个集合中的元素。参加跳舞的同学就是一个集合。我们班全体同学就是一个集合，我们班全体女生也是一个集合，我们班全体男生也是一个集合。

难道集合只能是人组成的吗？当然不是。书架上的书是一个集合。所有大大小小的长方形是一个集合。所有2 的倍数是一个集合。像这样，把指定的具有某种性质的事物看作一个整体就是一个集合。正如刚才同学们所表示的那样，集合有用文字表示的，有用符号表示的，还有用维恩图来表示的，你知道维恩图是怎么产生的吗？

（介绍维恩图）

【设计意图：集合作为现代数学的基本语言，可以简洁、准确地表达数学内容。学生先尝试用图展示集合模型，找到集合的知识核心，《集合的故事》用儿童化的语言讲述生活中的集合故事，介绍维恩图的由来。学生在自己尝试的基础上再听一听《集合的故事》，不仅为自己的创举自豪，而且很快被维恩图所吸引。】

3.板演维恩图的形成过程。

师：今天老师也带来2 个集合圈，红色圈内表示参加唱歌的同学，蓝色圈内表示跳舞的同学，怎样正确表示唱歌、跳舞的维恩图呢？谁上来摆一摆？

师：这两个同学为什么在两个圈里？

生：因为他们两个两项节目都参加了。

4.认识维恩图各部分的含义。

师：大家仔细观察这个维恩图，你在图中能够找到几个大大小小不同的集合圈？可以和同桌交流一下，并用手圈一圈。

师：你认为几个？

生：三个。

师：有没有更多的？

生：五个。

师：那我们就请五个的同学来汇报一下。大家还有需要补充的吗？

师：你能像刚才同学那样用手圈一圈再完整地说一说吗？

师：在这个维恩图中，我们找到大大小小不同的六个集合圈。

【设计意图：皮亚杰说：儿童的思维是从动作开始的，切断动作与思维的联系，思维就不能得到发展。教师提供两个实物圈，让学生亲手摆一摆集合圈，在动中学，在摆中思考集合圈各个部分的含义，集体讨论找出大大小小不同的集合圈。】

三、拓展提升，发散思维

师：回到课前同学们猜的，7人的情况我们已经解决了，如果是9 人、8 人、6 人、5 人，又是怎样的情况呢？如何用图来表示呢？你想自己研究一下吗？

（媒体动态演示变化过程，定格表格图）

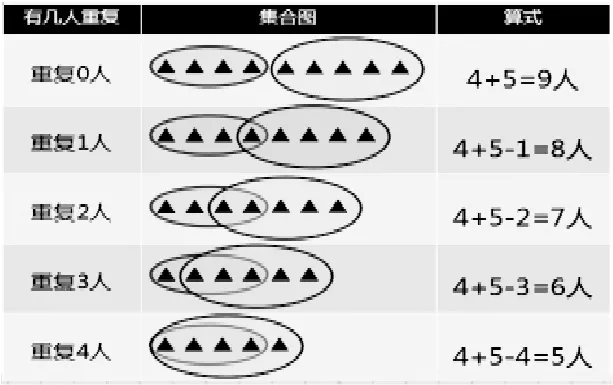
师：从这些图中，你发现了哪几个图很特别？

生：第一个图和最后一个图。

生：最后一个图就是说唱歌的所有人都是跳舞的人。

师：哦，原来跳舞的同学包含了唱歌的同学。

师：之前我们猜的，现在你能明白有这些可能了吗？

小结：用维恩图在解决问题过程中能够直观清楚地描述出它们之间的关系，并且会根据具体的情况呈现出不同的方式，可见维恩图在解决集合问题时非常有用。

【设计意图：知识的学习不能停留在一点，应触类旁通。教师为学生提供了集合可能产生的所有类型，帮助学生进一步建立集合的模型思想。集合分不交集情况、交集情况、包含情况，教师用同一件事，不同的人数，通过学生的独立思考、合作交流，采用画图、计算的方法再次验证了维恩图的神奇作用。】

四、联系生活，应用提升

1.动物问题。

师：（出示一组动物图片）这些动物有会游泳的，有会飞的。老师这里有两个维恩图，你会选哪一个？

生：选B，因为这些动物中既有会飞的，也有会游泳的。

师：你是分析了这些动物的特点之后决定选B 的。

师：（指图B）左边这个圈表示会游泳的，右边这个圈表示会飞的，那中间这一部分表示什么？

生：这些动物既会飞又会游泳。

师：又来了一只长颈鹿，我们应该把它放在哪个位置呢？为什么呢？

生：放在维恩图外面，长颈鹿是既不会游泳也不会飞的动物。

师：原来，维恩图的外面也可以表示有用的信息！

师：如果老师在这幅维恩图外再加一个集合圈，你认为它表示什么意思呢？

生：整个动物界。

师：同学们真是太棒了，会活学活用，集合问题不仅在动物界有，在数的集合中也有。

2.数的集合问题。

师：这两幅维恩图你想选择哪一幅呢？请你在《学习单》上选一选，填一填。

师：如果让你提出一个问题，你想提出一个什么数学问题呢?

生：一共有多少个数？

【设计意图：练习中以学生熟知的大自然中的动物为例，巩固集合的相关概念，说明各集合圈所代表的含义，使学生在有趣的、贴近生活的情境中，真正感受数学与生活的密切联系，提高应用意识。】