基于贝叶斯网络的机动岸舰导弹兵力作战效能评估∗

曾家有 刘天庆，2

（1.海军航空大学 烟台 264001）（2.92941部队 葫芦岛 125001）

1 引言

随着机动岸导兵力作战空间和远程对海打击能力的拓展和提升，其在海上封锁、岛礁攻防、基地防御、抗登陆、打击敌海上舰船编队等作战行动中的重要性更加凸显，尤其是机动岸导兵力强大的火力覆盖能力能够对海上来袭舰艇形成有效威慑[1]。然而，实际组织机动岸导与舰艇的对抗演练难度较大，过程也相当复杂，在缺乏实战依托的情况下，单单通过装备测试和实装演习对机动岸导兵力作战效能进行评估，不仅耗时耗力，而且由于作战过程存在大量复杂性和不确定性因素，基于小样本的试验很难得出科学合理的结果[2]。因此，选取科学有效的机动岸导兵力作战效能评估方法，对于助力岸导指挥员决策具有很强的现实意义。

近年来，部分国内文献就机动岸导的作战效能开展了相关研究，文献[3]运用层次分析法给出了机动岸导发射阵地的定量选择模型；文献[4]依据模糊层次理论建立了岸导武器系统的作战效能评估模型；文献[5]针对实战化条件下岸导训练需求，建立了相应的评估指标体系。然而，上述研究大都是基于岸导武器系统的效能评估，很少见到以岸导兵力作战效能评估为主要内容的研究。

本文采用贝叶斯网络模型，依据机动岸导兵力的特点及作战流程构建效能评价指标体系，进而建立评估模型，可在满足时效性要求的前提下对机动岸导兵力的实际作战效能进行分析评估。

2 贝叶斯网络概述

贝叶斯网络是一种应用范围较广的不确定性因果关联模型，其数学依据是概率论，建模与分析的核心是用条件概率分布来表达各个信息要素之间的相关关系，能够处理有限的、残缺的信息条件下的不确定性复杂问题[6]。

图1 三节点的贝叶斯网络结构图

对于离散变量，在给定其父节点状态时，该节点与其父节点的条件概率表反映了该节点与其父节点因果关系的强弱，若无父节点则节点状态为其先验概率。

假定一组有限离散随机变量的集合为X={X1,X2,…,Xk}，xi是Xi状态的取值，则p{X1=x1,X2=x2,…,Xk=xk}表示相关变量间的联合概率，Pai为节点Xi的父节点。此概率可以用条件概率链表示为

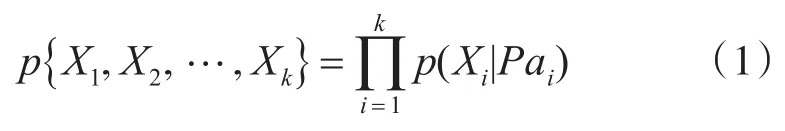
3 贝叶斯网络效能评估模型的构建

运用贝叶斯网络评估机动岸导兵力作战效能时，其建模流程可分为三步。Step1：确定影响机动岸导兵力效能评估的要素（贝叶斯网络的节点），并确定各要素状态的可能取值；Step2：将各要素间的因果关系转换为较为直观的拓扑结构图；Step3：确定父节点的先验概率和子节点的条件概率。

3.1 机动岸导兵力作战效能影响因素分析

一般来说，机动岸导兵力作战使用过程可划分为三个阶段：战斗准备阶段、战斗实施阶段、总结阶段[7]。战斗准备阶段主要完成战备等级转进、计划组织战斗等工作。战斗实施阶段主要工作包括机动开往待机阵地、待机阵地隐蔽待机、开往发射阵地、发射阵地展开、完成发射准备和导弹发射控制任务、按照命令撤离发射阵地等。总结阶段主要包括机动返回待机阵地或驻地、上报战斗要报等。具体作战流程如图2所示。

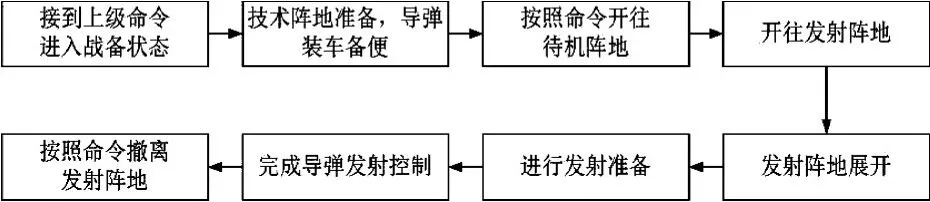
图2 机动岸导兵力作战流程图

分析机动岸导兵力的作战流程，影响其作战效能的因素很多，应着重从中选取能够反映机动岸导兵力特点、有实际背景依托的影响因素[8]。本文将机动岸导兵力作战效能划分为信息保障能力、对海突击能力、战场环境适应能力和战场生存能力等4个二级评价指标。

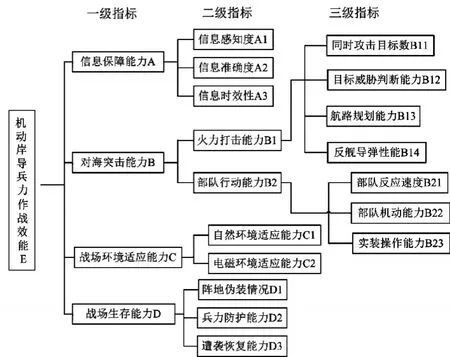
图3 机动岸导兵力作战效能评估影响因素

其中，信息保障能力是岸导兵力作战的重要支撑，若无法获得可靠的目标指示信息，机动岸导兵力将基本丧失作战能力，其影响因素主要为信息感知度、信息准确性和信息时效性。影响对海突击能力的主要因素为火力打击能力和部队行动能力；其中，火力打击能力主要包括同时攻击目标数、目标威胁判断能力、航路规划能力和反舰导弹性能等，部队行动能力主要包括部队反应速度、部队机动能力和实装操作能力等。对于战场环境适应能力，主要从自然环境适应能力和电磁环境适应能力两方面进行评估。对于战场生存能力，其主要影响因素为阵地伪装情况、兵力防护能力和遭袭恢复能力等。具体影响因素的选取如图3所示。

3.2 模型参数的设定

贝叶斯网络中，根节点的先验概率和子节点的条件概率（CPT）是进行最终评估的基础。本文采取基于隶属度加权的根节点先验概率求取方法，具体求解步骤如下。

3.2.1 确定属性等级

经岸舰导弹研制、作战使用等领域的权威专家判断，采用模糊分类的方法，建立机动岸导作战效能主要影响因素的属性等级集合。其中一个影响因素的属性集合为W={W1,W2,…,Ws}，其中Wi(i=1,2,…,s)为属性等级评语[9]。图3给出的主要评价指标中，机动岸导兵力作战效能E=｛好，一般，差｝，信息保障能力A=｛强，一般，弱｝，对海突击能力B=｛强，一般，弱｝，战场环境适应能力C=｛强，一般，弱｝，战场生存能力D=｛强，一般，弱｝。

3.2.2 采用熵权法确定根节点子指标的权重

首先统计子指标数据，并进行无量纲处理[10]，得A=(aij)m×n：

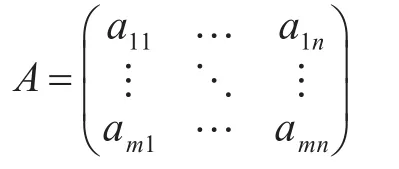
其中m（m≥10）表示专家数量，n表示根节点的n个子指标数量。

采用熵权法确定A中各子指标的权重，第j个子指标的信息熵为

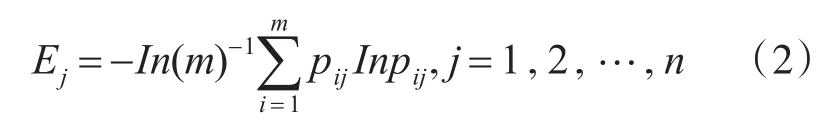
信息熵冗余度：

第j个子指标的权重为

3.2.3 计算根节点的先验概率

主要采用基于隶属度加权的方法[11]。第j个子指标隶属于等级Wi的隶属度为γij，通过子指标隶属度加权可以求得根节点属于等级Wi的先验概率为

故根节点的先验概率为

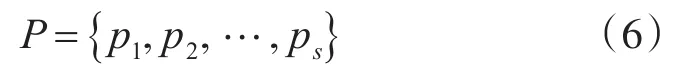
3.2.4 确定子节点的条件概率

通过邀请专家打分和统计处理的方法，确定子节点的条件概率。其中，m11表示在X1和X2属性为好的条件下，m个专家（m≥10）中有m11个专家认为X3的属性为好。对根节点子指标的进行打分以及确定子节点的条件概率，采用的是基于专家咨询和经验知识的德尔菲法，加之各影响因素的属性等级集合采用模糊分类的方法，难免带有一定的主观性[12]，但经过多组样本数据反复调试后，可以提高评估结果的可信度。由专家打分方式形成的条件概率如表1所示。

表1 节点X3的条件概率

其中，m11表示在X1和X2属性为好的条件下，m个专家中有m11个专家认为X3的属性为好。

3.2.5 求解效能评估结果

通过求得根节点的先验概率和子节点的条件概率，由式（1）和（2）可以计算出机动岸导的作战效能。

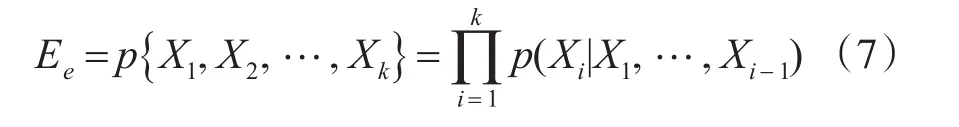
4 算例分析

本文假定机动岸导兵力领受对海突击任务，需评估其作战效能。以节点B1为例，首先邀位机动岸导的研制和使用专家成评估组（专家数量m=10），采用模糊分类的方法建立子指标 B11、B12、B13、B14的属性等级集合，规定75分以上为好，75分以下为差[13]，如表2所示。

根据表2给出的子指标数据，通过式（2）～（4）计算可得根节点B1的子指标权重为

根据表2中的数据和评价等级规定，可得到节点B1的子指标隶属度[14]，如表3所示。

表2 根节点B1的子指标数据

表3 根节点B1的子指标隶属度

根据式（5）计算得节点B1的先验概率为PB1={0 .599,0.401}。同理，根据专家组给出的分值，通过式（3）～（5）可得到根节点B2的先验概率分布，PB2={0 .571,0.429}。

B1、B2的先验概率确定后，由专家组确定叶节点B的条件概率表[15]，如表4所示。

表4 叶节点B的条件概率

确定条件概率表后，由式（7），可得到节点B的效能评价结果：EB={0.435,0.272，0.293}。同理，根据专家评分确定出父节点A、C、D的效能评价结果后，由条件概率表可得到机动岸导兵力作战效能的评价结果。

根据以上给出的求解步骤，利用可视化程度较好的Netica软件进行仿真运算[16]，步骤如下：

1）根据图2给出的评估影响因素建立贝叶斯网络有向无环图（DAG）。

2）输入根节点的先验概率及子节点的条件概率。因篇幅限制，先验概率及条件概率的求解及输入过程不一一列举，仅列举节点E的部分CPT输入过程，如图4所示。

3）完成参数输入后，运行仿真软件，即可得到评估结果：E好=0.446，E一般=0.438，E差=0.116，如图5所示。

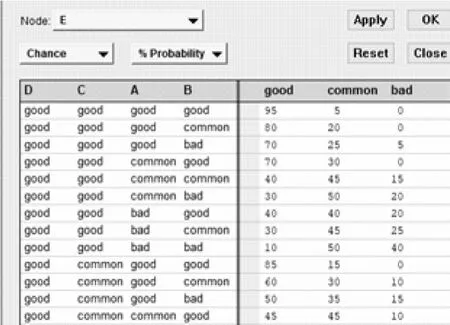
图4 节点E的部分CPT输入

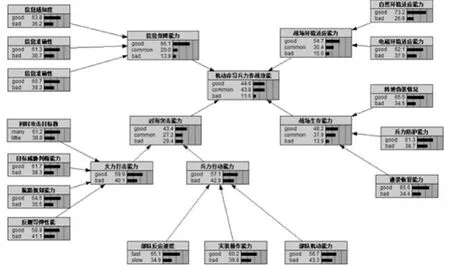
图5 仿真运算结果

通过实际算例可以看出，机动岸导兵力作战效能总评为好。随机更改节点A、B、C、D的参数设置，观察E的变化幅度，其中E随节点A和B的变化幅度较为明显，说明信息保障能力和对海突击能力对机动岸导兵力的作战效能影响较为显著，符合客观实际，证明该模型具有一定的合理性。

5 结语

本文依据机动岸导兵力组成和基本作战流程，梳理了机动岸导兵力作战效能评估影响因素，提出了基于贝叶斯网络的效能评价模型，对评估过程进行了具体描述，并通过实际算例，论证了评估方法的可行性。依据该模型，可对机动岸导兵力的作战效能进行初步评估，为指挥员决策提供参考依据。但是，组织机动岸导兵力作战是一个复杂过程，不确定因素和不可控因素较多，且利用贝叶斯网络进行评估时，难免会带有本领域专家的主观因素，因此，在科学、合理、客观地确定贝叶斯网络中的先验概率和条件概率[17]，提高评估模型的有效性方面，还需进一步结合实际数据进行反复检验，以此更新和优化整个评估体系。