特殊和一般的辩证方法在数学学习中的应用
魏选平
摘要:本文详细介绍了由特殊到一般的教学方法,在小学、中学及大学学习中的体现,反映出辩证的哲学思想,此方法对现实的数学教学具有很强的指导性。
关键词:特殊 一般 哲学 数学教学
一 引言
世界上任何事物都处于相互联系之中,矛盾的普遍性寓于特殊性之中,并通过特殊性表现出来,该规律在高等数学学习上也有指导意义。基于同类问题的最简单特殊问题与同类复杂问题间的平行的相似性,由最简单特殊问题研究、概括总结推广出同类复杂问题的解决方法。纵观各年级的数学学习,都先由特殊的实例概况归纳出本质规律,从而熟能生巧地总结概括推广出概念、定理,公式。这些定理、公式可解决同类事物中的所有复杂问题,由小学、初中、高中、大学数学的学习过程,无不体现出由特殊到一般,再由一般到特殊的规律。这种规律和方法具体体现在小学、初中、高中、大学数学学习的知识点和知识体系上。
二 小学、初中、高中、大学数学学习中的体现
1 小学学习中的体现
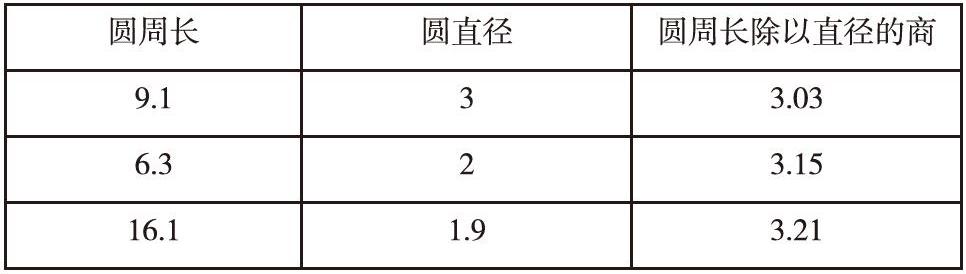
圆的周长公式也可由生活中的特殊到一般规律归纳出来。例如,车轮滚动一周的长度就是周长,如何测车轮周长用圆片试试看,圆片向右滚动一周,用线绕圆片一周可测量出圆的周长与直径有关,找3个大小不同的圆片分别测量出园的周长和直径,做一做,填一填。如下表 所示。
测量会有误差,可多测几次求平均值,会发现园的周长总是与直径的3倍多一点,从而得出圆的周长除以直径 的商是一固定的数,称其为圆周率,用字母表示,计算时常数取3.14,从而可用圆的周长公式求出所有圆的周长。该例从生活中的简单的特例概况出圆的周长公式。利用所求不同的圆的周长,这是由特殊到一般公式,再由一般公式到特殊问题的问题。
2 初中数学学习中的体现
勾股定理的學习可联系生活实际,对于任意三角形,只要是直角三角形,它的三边的长度就为一对勾股数,反过来,只要一三角形的三边长互为勾股数,则该三角形一定是直角三角形。从而总结出勾股定理。即任意直角三角形中,两直角边的平方和一定等于斜边的平方。由勾股定理可解决不同直角三角形的边角问题,尤其是从直角三角形的形状特性可总结出其性质规律,由勾股定理和直角三角形的性质可解决所有直角三角形问题。这是由特殊到一般公式,再由一般公式到特殊问题的问题。
3 高中的体现
初中七年级下册讲了变量的关系,变量的三种表示方法(解析式、列表法、图像法),也是高中的幂函数、对数和指数函数、三角函数的表示方法。对高中的幂函数、对数和指数函数、三角函数学习中,都可以用函数表达式先列表,找出几个特殊的点,然后,用光滑的曲线连接起来,就构成了函数的图形,通过观察、分析、总结出函数图形的特征和本质,用自己的语言描述一下,就得到了函数的性质。那么,这种用变量的关系总结出的简单的方法,可以用到高中一般复杂函数的学习中。无不体现出由简单到复杂,由特殊到一般的学习方法。
4 大学高等数学学习中的体现
4.1 在学习导数的定义时,先通过讲曲线上任意一点处切线和变速直线运动物体的瞬时速度这两个实例,在通过观察、分析和总结这两个实例的共同的相似的本质和特征,在熟能生巧的基础上,按照由特殊到一般的方法推广和深入,从而用自己的语言概括总结出导数的定义。
4.2 在学习微分方程的概念时,先讲简单的实例,已知曲线通过一定点,且在该曲线上任一点处的切线的斜率,求这曲线的方程。这道实例的解的过程是,首先设曲线方程,再根据导数的几何意义列出微分方程,最后用数学方法解出微分方程的解。对于这样的简单实例的解题过程,加以概括、总结和提炼,按照由特殊到一般的方法加以推广和深入,也可得到适用于所有微分方程的本质概念。微分方程也是方程。所有微分方程和小学四年级的方程间具有平行的相似性。小学学过,含有未知数的等式是方程。大学的研究对象为函数,所以,含有未知函数导数的方程为微分方程;小学学过,能使方程成立的未知数的值为方程的解。同样,能使微分方程成立的未知函数的值为微分方程的解;小学学过,含有未知数的最高阶次数为方程的次数。同样,含有未知函数的最高阶导数的阶数为微分方程的阶数。显然,小学的简单方程和大学的微分方程间具有平行的相似性,由这种相似性,可以由小学的简单方程的学习,平行递推出大学的微分方程的学习,从而使微分方程的学习变得通俗易懂。
三 结论
综上所述,小学、初中、高中、大学数学学习中的知识点和知识体系都体现出了由特殊到一般,再由一般到特殊的规律,这就启示我们在数学学习中只有抓住同类简单特殊问题与一般复杂问题间的相似性,才能由小学、初中、高中的简单特殊问题的学习和研究,熟能生巧地推广和概括出大学的一般复杂问题的学习。小学、中学、大学数学学习中的每一个重要公式、概念、定理都是从生活中简单特殊的实例总结概括归纳出来的,由这些基本定理公式又可解决形形色色的同类所有问题。也体现出了由特殊到一般,再由一般到特殊的规律。只要掌握了从特殊到一般的方法,就能提高学生的自学能力,就能增强教师的教学能力。一般来说,特殊的实例都很简单,一般问题都很复杂,这种方法也是从最简单的问题中学会复杂问题的解决办法,这不能不说是一种智慧。有了这种智慧,不但能学好数学,也能学会分析和解决新问题的能力。

