随机振动响应峰值因子的预计理论研究

张玉杰，黄超广，段丽慧

（航空工业一飞院强度所，西安 710089）

在现代飞机结构设计中，需要合理地预估振动过程中可能的最大响应或应力，以便进行动载荷设计或动强度评估[1-2]。尤其对于具有不确定特性的随机振动过程（常用功率谱密度GPSD和均方根GRMS表征）[3-4]，准确预计最大振动响应，则显得更为重要。

对于随机振动，通常采用GRMS的放大倍数（峰值因子）来预计响应峰值[5]。传统方法采用3GRMS准则，即设定峰值因子为3。其数学内涵为高斯随机变量在（–3GRMS，3GRMS）区间外取值的概率（超越概率）为0.27%。由于涉及概率问题，3GRMS准则一直饱受争议。Himelblau、Fackler、Lubrs 等[6-8]推荐使用3RMS 准则。麦道公司[9]采用4GRMS确定最大等效静载。Scharton[10]设定峰值因子为 5。DiMaggio[11]和Ahlin[12]则提出了不同的峰值因子预计理论。

目前在飞机设计中，可供参考的一类预计随机振动响应峰值的方法是根据指定的超越频次或超越概率指标。例如， 对于连续突风载荷设计， FAAADS-53[13]推荐的超越频次为2×10–5次/飞行小时。F-22 抖振强度设计[14]中给出的超越指标为全寿命周期内超越概率为10–4。

下面简要研究目前几种实用的峰值因子预计理论，以便指导随机振动下结构的动强度设计。

1 理论分析

1.1 超越概率理论

假设随机振动过程满足某种分布，常用分布包括高斯分布、瑞利分布和威布尔分布，根据分布的超越概率预计峰值因子。标准瑞利分布下幅值A大于λGRMS的超越概率表达式为：

因此，峰值因子λ与超越概率P之间的函数关系为：

表1 显示了高斯分布和瑞利分布下，不同峰值因子对应的超越概率。可见，超越概率越小，峰值因子越大。相同超越概率下，瑞利分布对应的峰值因子大于高斯分布。

表1 峰值因子与超越概率Tab.1 Peak factor and exceeding probability

1.2 超越频次理论

超越频次是指单位时间（秒）内超越某个幅值的次数，表达式为：

式中：N为时间段T内的超越次数。

结合超越概率的含义，可得超越频次与超越概率的关系：

式中：vp为单位时间内幅值出现的平均次数。由随机振动理论可知，vp可表示为振动响应GPSD谱矩的形式[15]：

将式（1）所示的瑞利分布超越概率代入式（4），可得：

设定时间段T内的振动响应峰值的超越次数N=1，则式（6）变为：

因此，峰值因子的表达式为：

由式（8）可知，对于同一组振动信号样本，峰值因子λ随信号作用时间T的增长而增大。

1.3 损伤等效理论

文献[16]基于高斯分布和损伤等效原则，给出了峰值因子的表达式：

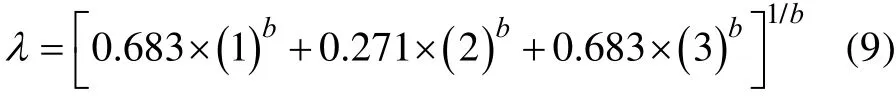
式中：b为材料疲劳S-N曲线的斜率，通常取4~12。

文献[17]介绍了一种快速近似计算随机疲劳寿命的方法，简称三段法。该方法同样基于高斯分布假设：1 倍、2 倍、3 倍均方根振动应力水平（简写为1σ、2σ、3σ）在总循环次数N中的占比分别为68.3%、27.1%、4.33%。由此给出的峰值因子的表达式为：

比较式（9）和式（10）可知，文献[16]将3σ的占比由4.33%误写为68.3%，显然是不对的。

表2 显示了不同b值下由式（10）计算得到的峰值因子。可见，λ随b的增大而逐渐增大，但增幅较小，λ最大值小于3。从物理含义上讲，式（10）所示的峰值因子是用来衡量整个振动过程的平均损伤，不适合表征振动响应峰值与RMS之比。

表2 不同b 下的峰值因子Tab.2 The peak factors under different b

1.4 GPSD 时域拟合理论

对振动响应GPSD进行数值变换模拟可以得到对应的时域样本。目前常用的GPSD时域拟合方法[18-20]包括：三角级数法、白噪声滤波法、二次滤波法、逆傅里叶变换法和蒙特卡洛法。提取时域样本的绝对最大值Gmax和均方根GRMS，由式（11）计算峰值因子：

1.5 三角级数理论

文中基于三角级数提出一种预计峰值因子的方法。理论上任意振动信号均能写成三角级数的形式：

式中：A为幅值；ω为圆频率；φ为相位；n为总级数。

若认为信号频率较为离散，耦合效应微弱，满足工程常用的稀疏模态假设，则y(t)的最大值为各个正弦信号幅值之和：

y(t)的均方值为各个正弦信号均方值之和。因此，y(t)的均方根为：

保守起见，可取式（17）上限 2n预计峰值因子。可见，峰值因子λ只与信号中包含的峰值频率个数n有关。特别地，对应单频简谐信号（n=1）， 2λ= ，即幅值与均方根之比为 2 ，符合实际。

2 案例分析

图1 显示了某型飞机在试飞过程中测得的加速度时间样本，时间长度为16 s，采样频率为6144 Hz。图2 显示了不同样本长度对应的GPSD，具体采用MATLAB 中的Pwelch 函数进行计算。可见，不同样本长度下的GPSD曲线基本吻合，表明样本属于平稳随机过程。

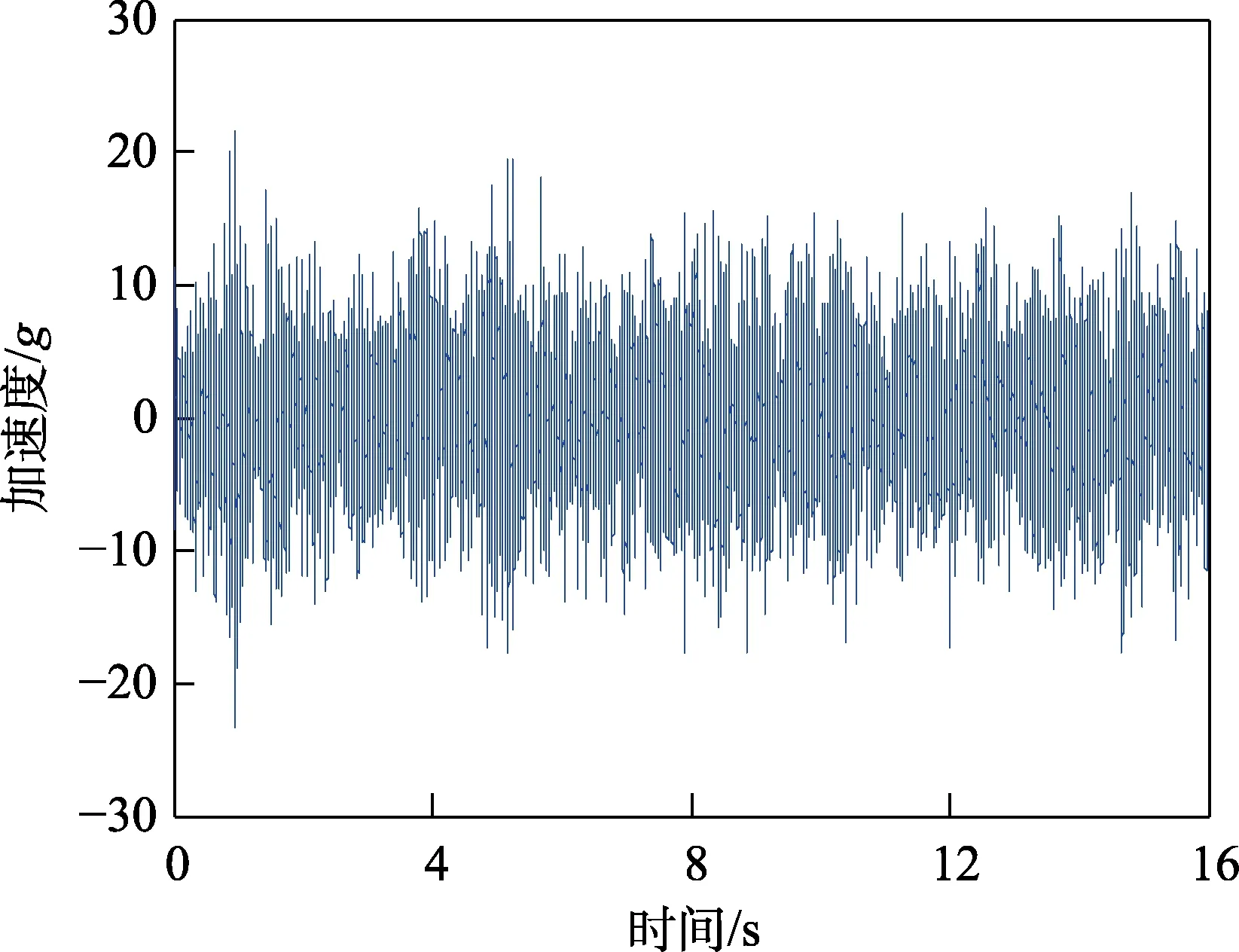
图1 振动加速度时间样本Fig.1 Vibration acceleration time sample

图2 不同样本长度下的PSDFig.2 The PSD’s Under different sample length

以图2 所示4 种不同长度样本对应的GPSD作为输入，研究超越频次理论和PSD 拟合理论预计的峰值因子。这里采用逆傅里叶变换法对GPSD进行时域拟合。图3 显示了样本长度8 s 对应的原始GPSD和时域拟合，可见，两者吻合度较高。表3 对比了峰值因子的真实值（基于测试时域样本）以及两种理论的预计值。可见，基于GPSD时域拟合理论预计的峰值因子似乎更接近真实值。需要注意的是，由于GPSD时域拟合计算中假设相位随机，因此，每次拟合得到的时域信号不尽相同，导致峰值因子也存在差异。

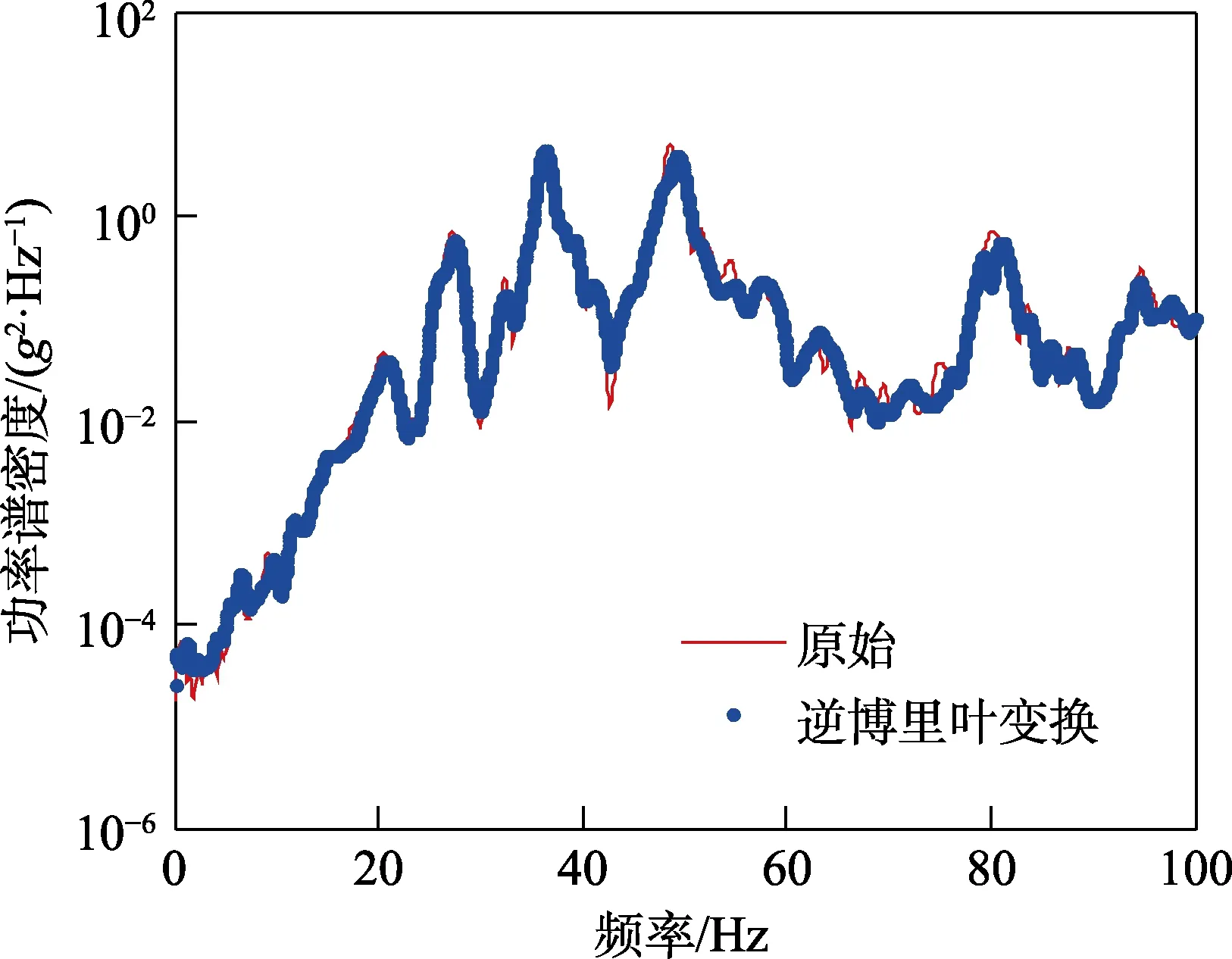
图3 原始PSD 与时域拟合后PSD 的对比Fig.3 Comparison between original PSD and fitted PSD

表3 峰值因子对比Tab.3 Comparison of peak factors

针对图3 中8 s 样本的GPSD，分别进行10、100、1000、10 000 次逆傅里叶变换，记录每次的峰值因子，得到4 组峰值因子样本。分析表明，每次拟合得到的时间历程，其均方根值恒定，最大值不同。因此，峰值因子的差异主要由最大值引起。将每组的峰值因子λ按从小到大的顺序排列，定义归一化次数k为排序号i与总数n的比值（i≤n，n=10、100、1000、10 000），此时k在统计学上称为累积概率，与前文中超越概率P之间的满足关系：k=1–P。

λ随k的变化曲线如图4 所示，可见，λ随着k的增加而增加，增幅逐渐增大。当k>0.9 之后，增幅急剧变大，λ最小值约为2.9，最大值约为5.3。4 组曲线基本重合，并且从变化特征上满足某种指数分布。图5 显示了采用高斯分布对数据进行拟合的结果，可见，k随λ的变化曲线满足高斯分布。因此，采用GPSD时域拟合理论预计峰值因子本质上仍属于概率问题。

下面采用三角级数理论预计峰值因子。由图2 可以看出，GPSD曲线中包含9 个较为明显的离散峰。因此，根据式（17）计算得到λ=4.243，与4 组样本峰值因子真实值的平均值4.092 的相对误差为3.69%，从而验证了所提方法的有效性。该方法的不足在于，缺乏离散峰个数的合理判据。后续将针对该问题展开进一步的研究。

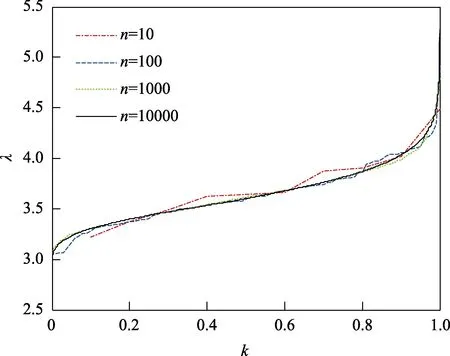
图4 峰值因子随归一化次数的变化曲线Fig.4 Variation curve of peak factor with normalization times

3 结论

简要介绍了4 种峰值因子预计理论，并基于三角级数理论提出一种新的预计方法。结合试飞振动数据进行了类比分析，所得结论如下所述。

1）超越概率理论、超越频次理论、损伤等效理论和PSD 时域拟合理论本质上属于统计学理论，峰值因子与概率分布密切相关。

2）基于GPSD时域拟合理论预计的峰值因子波动较大，根源在于拟合得到的时域最大值不同，峰值因子与归一化次数（累积概率）满足高斯分布。

3）所提三角级数理论能够较好地预计峰值因子，但离散峰个数缺乏合理判据，需要开展后续研究。