基于直升机耦合分析的振动响应预测研究

冯志壮，代志雄，刘晨

（中国直升机设计研究所 旋翼动力学重点实验室，江西 景德镇 333001）

自直升机问世以来，对其振动问题的研究就没有停止过，振动问题伴随着直升机整个研发、使用、维护等过程。常规单旋翼带尾桨直升机的振动激励主要有来源于旋翼的气动谐波载荷，通过主减等传递通道作用于机体，引起机体的振动响应[1-2]。机体的运动又会反馈到旋翼桨毂处，引起桨叶的运动，进而影响旋翼气动力的变化[3-5]。因此，直升机振动分析是一种旋翼与机体耦合系统的响应分析过程[6]。

最早的直升机振动问题的研究常常采用试验方法，研究成本和研究周期都较长。计算预测则采用直接法，即将孤立旋翼桨毂谐波计算结果作用于机体的桨毂处，得到弹性机体响应的谐波综合结果。该方法理论及计算简单，适合工程中简单的估算，但旋翼谐波载荷及复杂的机体建模都会影响计算的精度，且该方法常采用桨毂固定的方式计算桨毂力矩，得到的结果不能准确反映旋翼与机体之间的耦合作用[7-8]。因此不适用于定性预测分析，无法揭示机体振动现象的本质。

早期的旋翼/机体耦合动力学响应分析方法中，气动力均采用准定常或半经验公式，机体则采用刚体或基于梁单元简化模型，精度较低。耦合方法也有采用阻抗匹配法，该方法需首先得到机身在桨毂处的导纳及旋翼整体振型对应的阻抗[9]，适用于耦合系统的固有特性分析[10]。国内有采用多体动力学程序建立旋翼系统结构动力学模型[11-13]，柔性体采用Nastran 输出结果。该建模优点在于将结构模块化，增删结构方便，缺点在于无法反映桨叶旋转真实气动特性。目前我国正在积极开展直升机旋翼机体耦合动力学分析[14-17]及试验[18]相关研究，关于直升机振动响应预测的研究是基于旋翼与机体分开建模分析的方式。为了将直升机动力学、振动预测和减振等问题联系起来，目前亟需结合理论研究和试验验证的基于耦合建模的直升机全机动力建模分析技术。

文中针对直升机气动环境复杂、旋翼与机体结构耦合振动大的特点，基于气动时间有限元分析模块，耦合机体动力学建模结果，完成旋翼直升机旋翼机体耦合动力学分析模型。对背景直升机三个典型前飞状态进行了振动预测及与试验对比的分析研究。

1 耦合动力学建模

直升机在飞行状态下，各片桨叶的振动载荷在桨毂处合成、滤波，再经桨毂传向机体，引起整机振动。为了研究旋翼机体耦合振动特性，需要建立有效的动力学分析模型。建立旋翼系统与机体结构耦合动力学分析模型的具体思路如下所述。

机体结构、旋翼系统动力学模型：机体结构动力学模型是振动控制综合分析模型的基础模型，采用有限元法建立。针对某型直升机，直接采用Patran 建立机体结构动力学模型，分析提取机体动力学特性参数。旋翼动力学模型根据旋翼机体耦合动力学建模研究思路及需求，采用15 自由度中等变形梁模拟旋翼结构，结合动态入流理论建立对应的旋翼动力学分析模型。

耦合动力学模型：在Patran 中以自由无约束模型计算机体结构的动力学特性，根据旋翼的动力学特性，筛选出机体主要刚体模态及弹性模态的振型，提取关键点模态参数，编制机体关键点振动数据库，耦合到旋翼动力学分析模型中，进而形成耦合计算程序。为了减少方程中的变量数目、简化计算，文中所有参数均已无量纲化。

1.1 旋翼动力学有限元模型

建立可靠的动力学模型，是准确预估直升机动力学响应，进而设计高效的减振措施的前提和基础。文中以某型直升机旋翼为原型，以中等变形梁理论建立了相应旋翼结构动力学有限元模型，如图1 所示。

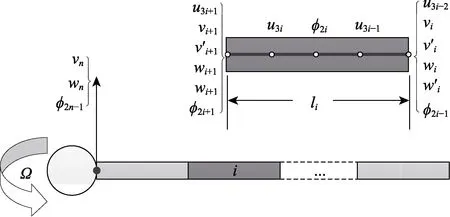
图1 旋翼结构有限元模型Fig.1 Finite element model of rotor wing structure

将以Ω为转速绕桨毂旋转的桨叶划分为N段梁单元，长度为li。对于非根部的第i段旋翼单元，有由轴向运动u、扭转运动φ、摆振方向运动v及挥舞方向运动w组成的15 自由度单元，保证了单元间相互运动的连续性。对于不同形式旋翼桨毂的连接处，采用不同的建模方式。以文中铰接式旋翼为例，铰接点为根部旋翼单元，因此删除第N段桨叶左端自由度，增加挥舞、摆振及扭转自由度。

桨叶的气动力模型采用考虑了环量力与非环量力的准定常模型，为对比计算结果与试验值，入流模型采用Pitt 动态入流模型[19]，通过时间有限元法[20]，求解桨叶的气弹响应。得到时间有限元自由度下的桨叶模态响应函数为：

式中：d(x)为模态响应函数收敛判定函数。

再根据旋翼模态振型，将桨叶模态响应函数还原为桨叶中等变形梁自由度下的加速度、速度、位移响应。根据计算所得位移、速度、加速度等计算桨叶载荷谐波值。通过已知桨叶的速度、加速度及相应的入流信息，计算桨叶各剖面的来流速度。通过高斯积分的方法，将由来流速度引起的气动力积分，得到桨叶的总气动载荷（桨根力及力矩）。

通过已知桨叶的速度、加速度、位移可以求得桨叶的惯性力，与上述桨叶气动力求和，可得桨叶的根部受合力情况。根据桨叶载荷，拟合求解桨毂总的谐波载荷FH为：

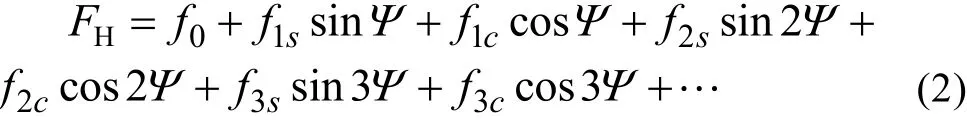
式中：fn为旋翼载荷的n阶分量，n=0 为均值，nΨ为旋翼旋转倍频相关谐波量。

1.2 机体起落架动力学有限元模型

以某型直升机为例，在Patran 中建立了机体结构的有限元模型，机体结构动力学模型包括除主旋翼以外的结构。本算例涉及的机型可分为尾段和机体段，尾段细长，且主要由承力结构组成，以梁单元、壳单元及集中质量来模拟。机体段结构非常复杂，比尾段结构短，而外形尺寸大，几乎直升机的全部装载质量都集中在机体段。起落架采用前三点式起落架，两者以梁单元加MPC 连接杆及集中质量来模拟。根据该型机特点，选取10 个机体点（见表1），作为考察的关键点。

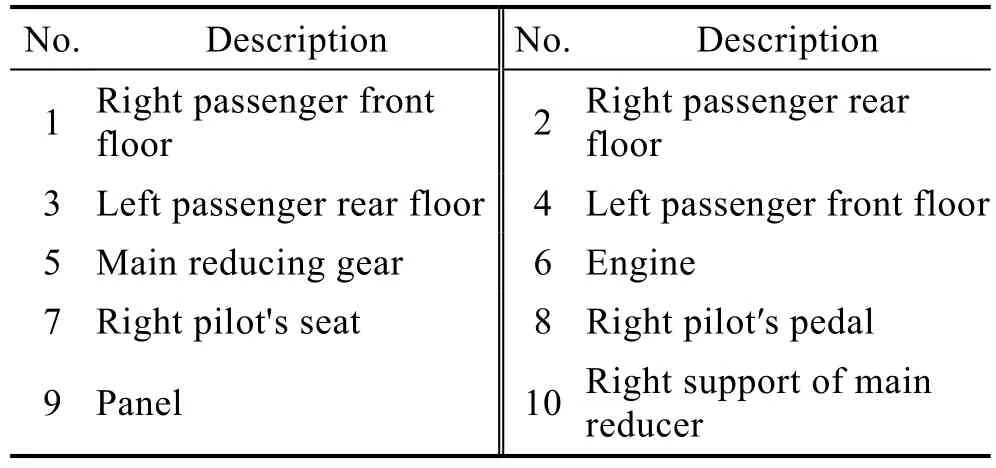
表1 直升机机体考察关键点Tab.1 Key inspection points of airframe

耦合计算过程中，选取包括了机体主要振型的前20 阶（100 Hz）作为机体动力学耦合部分。机体前8阶模态频率计算值与试验值（去掉试验值中局部模态结果）对比结果见表2。

表2 机体固有频率计算结果（单位：rev-1）Tab.2 Natural frequency calculation results of airframe (unit: rev-1)

通过上述对比可以发现，机体模态计算结果与去掉局部振动模态试验结果基本一致，证明本有限元仿真计算结果能有效反应直升机机体真实的结构动力学特性。

在上述机体结构动特性分析的基础上，从机体结构动特性计算结果中选取刚体和弹性模态的总阶数、模态质量、模态阻尼、模态频率，以及对应这些模态的桨毂中心模态位移。为了建立耦合分析模型及对比2 倍旋翼转速频率下的机体响应结果，选取旋翼转速频率2NΩ范围内合适的模态，提取包含桨毂中心模态振型矩阵Φ、模态阻尼矩阵C、模态刚度矩阵K、模态质量矩阵M、频率等模态参数。得到关于机体的响应函数x为：

同样，将x写成与旋翼动力学分析相对应的谐波分量形式，则可表示为：

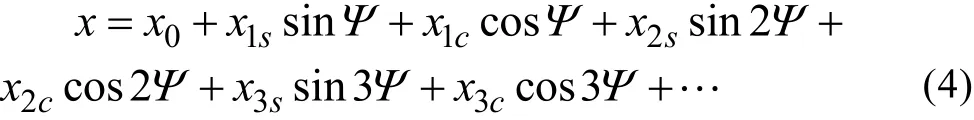
FH的第i阶谐波分量FHi引起的各阶模态的响应函数xi为：

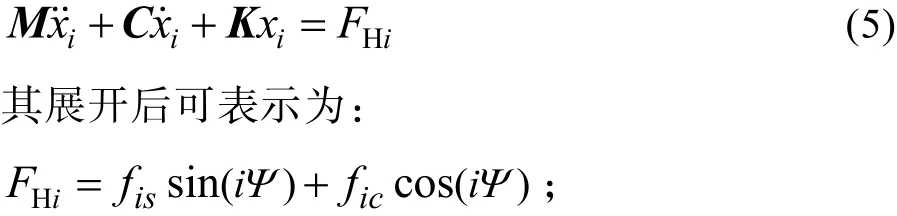
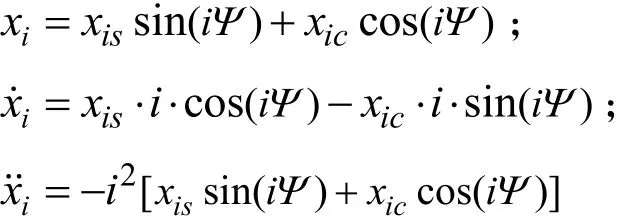
1.3 谐波法求解机体响应

根据上述机体谐波分量响应可知，代入可得展开形式的i阶谐波分量运动方程为：

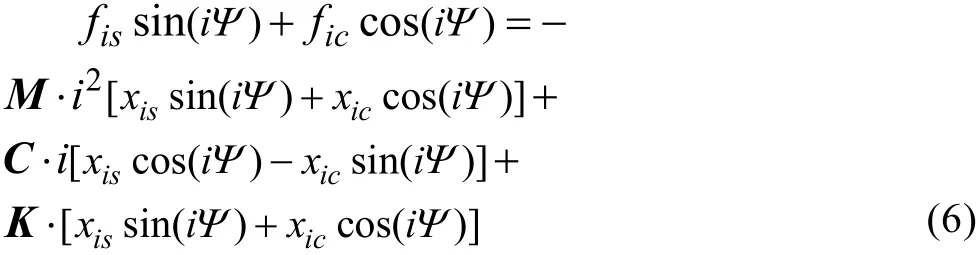
由高阶谐波分量iΨ不为0 可知：

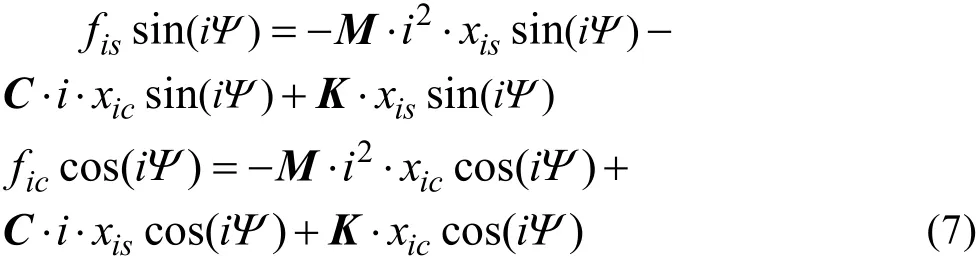
若要式（7）成立，必须保等式两边正弦与余弦分量的系数相等，则有：

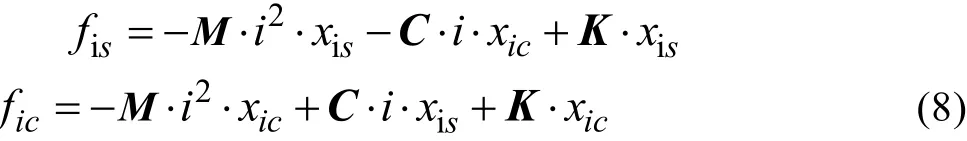
旋翼i阶谐波激励力在机体x阶模态产生的响应结果函数为：

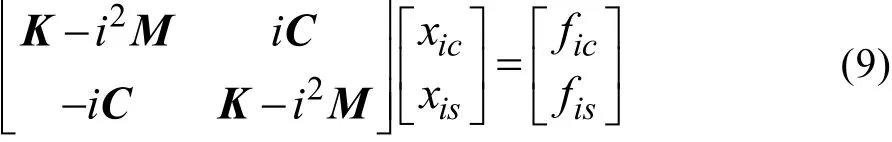
由此即可求得机体每阶模态的响应结果，以及谐波形式的响应速度、响应加速度。根据该谐波计算结果，即可求出对应的时间节点机体各点的响应以及桨毂处的节点响应。根据桨毂处的节点响应，可代入旋翼动力学模型中重新计算桨毂总的谐波载荷FH，得到新的机体模态响应结果，循环这一过程，迭代计算直至响应函数收敛，即可得到旋翼/有限元机体响应分析结果。

2 旋翼动载计算

文中以某型直升机为例，采用上述方法进行耦合动力学分析。通过旋翼动力学分析可以得到单片桨叶额定转速下在空中动特性计算结果，见表3。

从上述计算结果可知，采用文中计算方法得到的桨叶固有频率结果与试验值拟合较好，前六阶计算值误差小于5%。桨叶前六阶模态计算结果的振型（无量纲）如图2 所示。

表3 旋翼额定转速固有频率计算结果Tab.3 Natural frequency calculation results of rotor ring rated speed rev-1

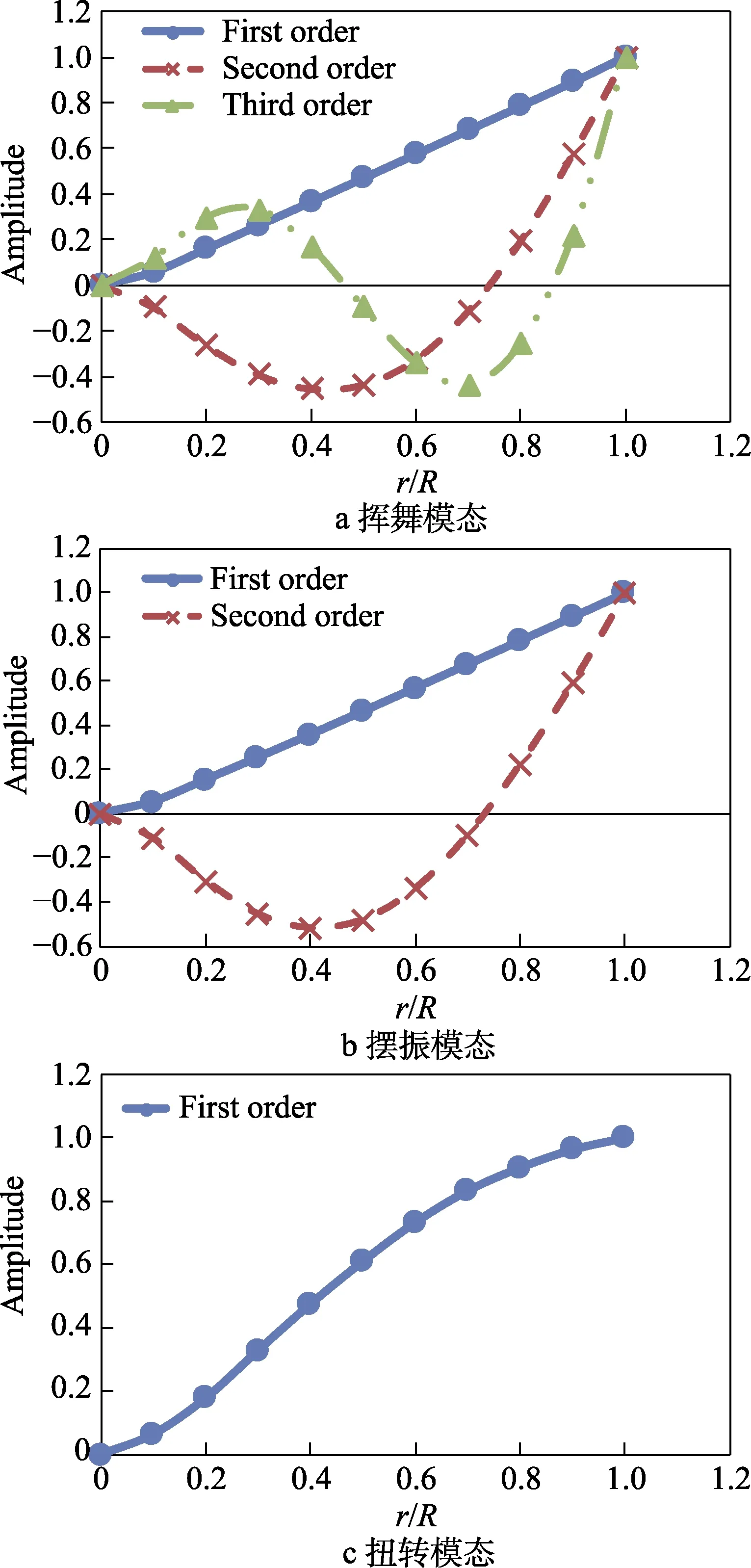
图2 桨叶前六阶模态振型Fig.2 The first six modes of blade: a) swing mode;b) shimmy mode; c) torsional mode

在桨叶结构动力学分析的基础上，进行了前飞状态的桨毂载荷分析。分别计算了直升机在前进比为0.22、0.275、0.302 三种前飞状态下的桨毂载荷，并以空机质量无量纲化。前进比为0.302 时桨叶根部载荷的计算结果（因为展向力主要为桨叶高速旋转产生的离心力，对机体振动响应影响较小，因此未列出）见表4。

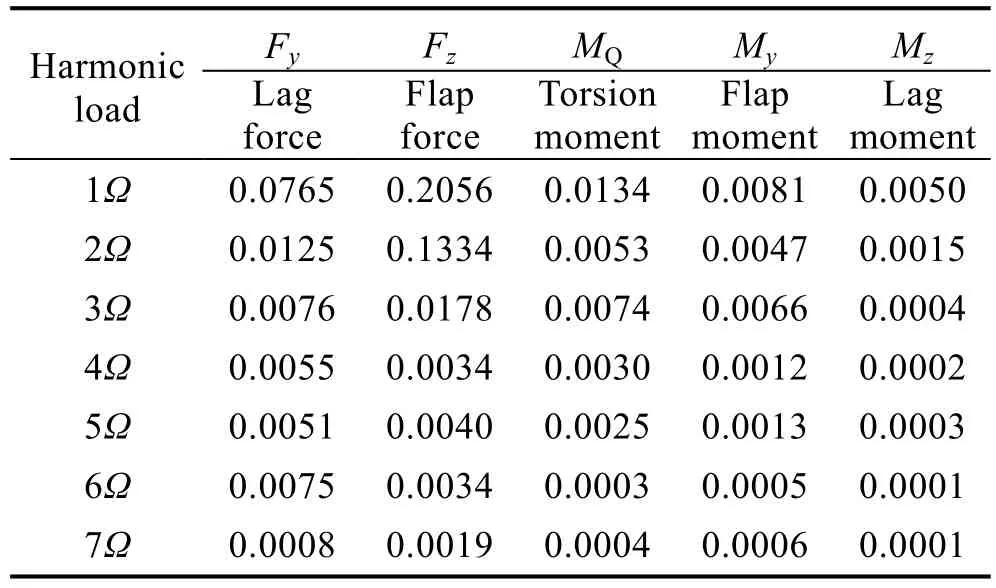
表4 桨叶根部载荷计算结果Tab.4 Load results of blade root

由图2 可知，桨叶摆振力及挥舞力谐波载荷逐级减小，同时旋翼垂向（挥舞力Fz）幅值比其他方向的载荷要大得多。提取桨叶中段桨叶载荷与试验值对比见表5。

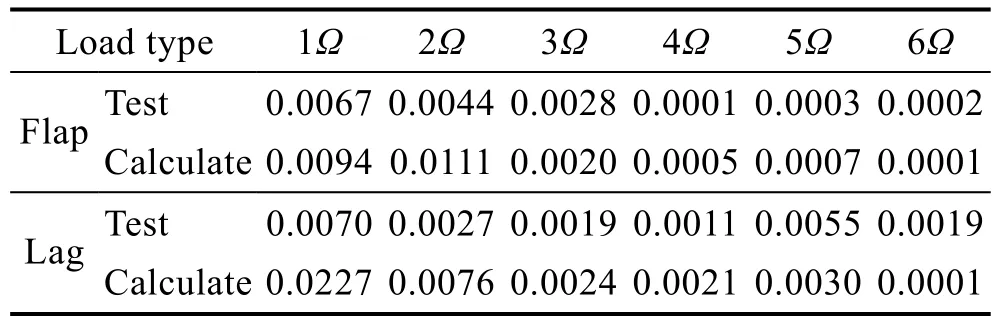
表5 桨叶中段载荷结果对比Tab.5 Load results of middle blade

从上述结果可以看出，计算值与试验值存在一定的误差。这是由于试验测试对应的真实飞行状态下，直升机处于相对平衡的状态，影响载荷因素（如自然风、飞控系统反馈等）时刻在变化。桨叶段挥舞及摆阵方向的载荷幅值随着谐波阶数的增加而减小，但试验值摆阵方向五阶载荷明显高于四阶，计算值也有相同趋势。分析原因可能为：旋翼摆阵三阶固有频率与之相近，使得振动放大导致的。而计算建模存在一定的误差，导致计算结果三阶与5Ω仍有2.26%的差别，因此放大效应小于试验值。

3 机体振动响应预测

在旋翼动力学分析的基础上，采用文中建立的耦合动力学模型，进行旋翼与机体耦合振动计算，分别计算了前进比为0.22、0.275、0.307 时机体的振动响应。提取前进比为0.307 时机体模型测量点的振动频谱，绘制如图3 所示的频率特征曲线。

由图3 可知，机体主要的振动频率为旋翼转速频率的整数倍。从计算值与试验值对比还可以得出，计算结果频率成分单一，不存在其他干扰频率。这与计算时采用谐波耦合方法，仅保留了桨毂载荷谐波成分有关。而试验状态下的激励不仅有来自主旋翼的振动载荷，还伴随有发动机转速频率的激励及尾桨激励。同时，试验数据机体上中减速器壳体的信号比较杂乱，这与壳体本身结构及安装有关。

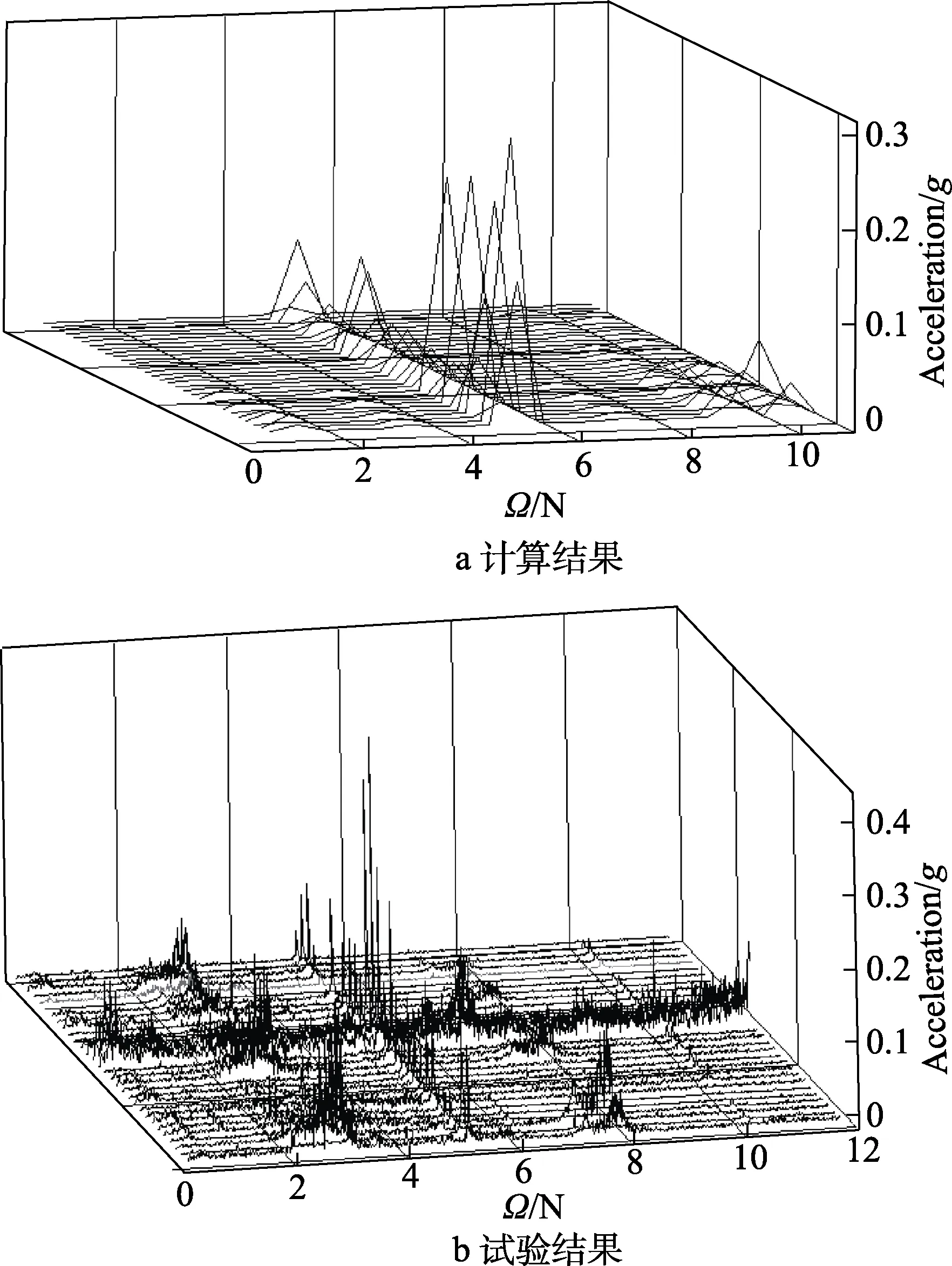
图3 机体测点振动频谱Fig.3 Vibration calculation results (a) and test results(b) of key points

前进比为0.307 时，NΩ与2NΩ试验值与计算值测点振动响应如图4 所示。

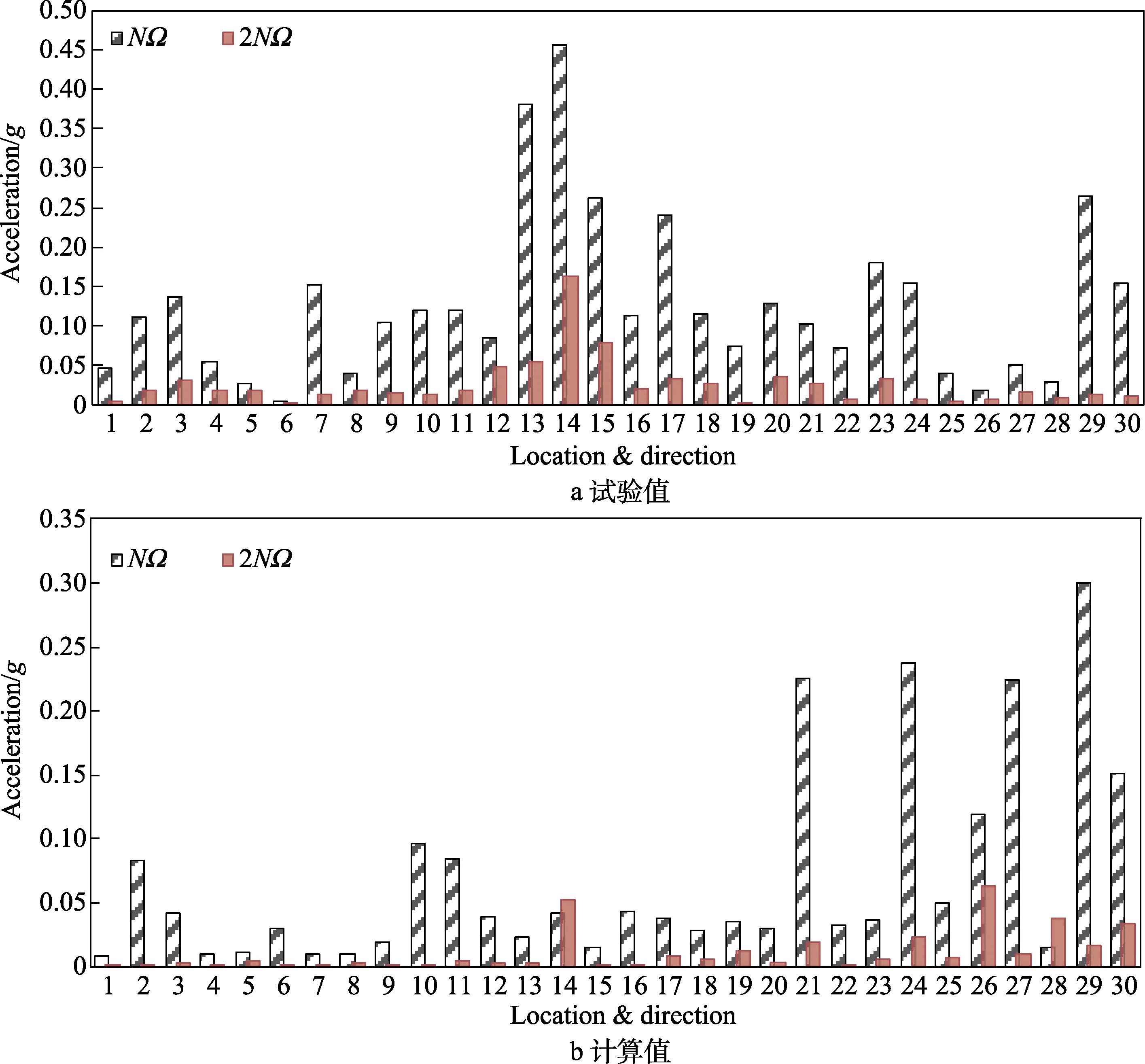
图4 前进比为0.307 机体测点振动响应Fig.4 Vibration test results (a) and calculation results (b) of key points at advance ratio of 0.307

由图4 可知，NΩ的振动响应明显高于2NΩ，这与桨叶剖面高阶载荷低于低阶载荷的规律一致。对比NΩ与2NΩ响应的计算及试验值可知，与频谱分析结果一样，部分测点的试验值与计算值存在较大差别，这与计算建模难以准确模拟机体的全部状态有关。

不同前进比时5Ω机体测点振动响应计算值与试验值的对比如图5 所示。

由图5 可知，在旋翼激振NΩ主振频率点，机体振动响应计算值与试验值变化规律相同，部分点存在较大差别（如中减速器壳体对应的13、14、15 通道）。初步分析产生这一现象的原因，是Patran 中的有限元模型不能真实地反映直升机该结构的安装及使用环境，导致以机体模态分析为基础的耦合分析产生误差，即耦合分析的准确性与机体有限元建模的精确性关系较大，但因为建模采用的是模态综合及传递率的方法，除桨毂外，其他各点之间相互影响较小。由图5 还可以得出，随着前进比增大，NΩ的振动响应随之平稳增大，其变化规律与桨毂激励载荷随飞行速度的变化规律一致。

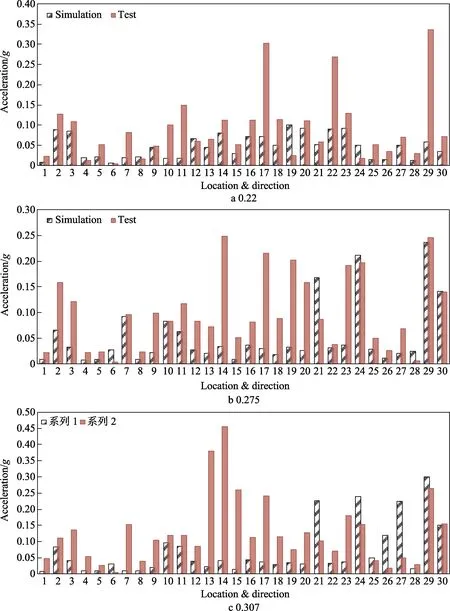
图5 不同前进比机体测点振动响应Fig.5 Vibration results of key points at different advance ratio

总之，采用文中方法预估的机体结构振动响应随飞行速度的变化、输出点振动量值分布，以及各点三方向的响应量值之间的关系，都符合真实的直升机振动响应变化及分布规律。这表明该方法在直升机响应预估上具有较好的实用性，但结果的准确性依赖旋翼模型及机体建模的准确性。

4 结论

针对直升机机体振动响应预测问题，建立了一种基于旋翼机体耦合动力学分析的全机振动响应预测方法。通过建立的计算方法，进行了背景直升机在三种前飞状态下的响应预测分析，同时通过与试验的对比分析，验证了该方法在揭示耦合振动问题的谐波响应本质问题。通过分析得到的主要结论如下。

1）桨叶载荷分析与试验值存在一定误差，这是由于模型难以模拟真实飞行环境，桨叶弦向力及挥舞力谐波载荷逐级减小，旋翼挥舞力幅值较其他方向的载荷大。

2）文中的耦合分析方法能有效地揭示旋翼机体耦合状态下的谐波分量关系，直升机机体响应以旋翼旋转主振频率NΩ 为主。

3）随着前进比的增大，背景直升机机体NΩ 的振动响应随之平稳增大，这与桨毂载荷随飞行速度增加而增加的变化规律一致。