基于SPIHT 的医学图像压缩算法研究与改进∗
王 玲 李 兵 罗 玉
(西华大学计算机与软件工程学院 成都 610039)
1 引言
现代医学中,医学影像检查如CT、MRI 已成为医生诊断和治疗的重要手段。尤其是大型医院每天面临大量的医学影像资料存贮,对所需的存储设备提出了更高要求。同时随着远程医疗服务的推行,医学图像传输对网络带宽和实时性提出了更高要求。为了节省存储容量,满足海量CT 图像数据长时间存档的需求,并且提高压缩性能,减少网络传输时间,医学图像压缩算法研究成为重要关注问题[1~2]。
文献[3]将医学图像分割为感兴趣区和非感兴趣区并对此分别采用无损压缩和有损压缩,在保证图像诊断效果的同时提高压缩比。文献[4]针对图像压缩质量提出一种奇异分解和Contourlet变化相结合的有损图像压缩方法,相较于单独使用这两种方法能获取更高的峰值信噪比。文献[5]进一步提出将离散小波变换(Discrete Wavelet Transform,DWT)、离散余弦变换(Discrete Cosine Transform,DCT)和奇异值分解相结合的有损图像压缩混合编码,明显改善系统的压缩比和计算时间。文献[6]通过遗传算法与Huffman 编码对医学图像中提取的感兴趣区域来进行无损压缩,相比现存的一些压缩方法有较高的压缩比。文献[7]基于最佳样条小波变换的改进设计了一种高效的编码解码器,相比JPEG2000 标准[8]中常用的双正交小波变换在同样压缩比下有更好的峰值信噪比。但上述这类基于软件思维设计的图像压缩方案难以从性能和速度上提高网络数据的传输效率,阻碍了远程医疗的在线服务[9]。为减少存储空间并获取更有效的传输性能,许多学者为此纷纷提出了基于硬件设计的图像压缩方案。文献[10]提出一种无乘法器、低复杂度的DCT 设计方案,并能通过GPU 快速有效实现。文献[11]对DWT 的存储要求和关键路径设计了一种内存高效的多层次结构体系,改进硬件性能,减少片上存储资源。文献[12~13]充分利用现场可编程门阵列(Field Programmable Gate Array,FPGA)并行、高速的片内资源,降低片外存储器的使用,为数据编码和传输提供了充分条件;文献[14]为满足复杂设计系统,利用片上系统(System on a Chip,SOC)实现SOC 的系统控制和FPGA 的运算处理,可方便图像数据的存储、压缩、显示,充分展现了SOC技术软硬结合的优势。
在上述图像压缩算法研究的基础上,文中主要从系统资源并行实现的角度,对医学图像压缩方法展开研究。利用FPGA 丰富的硬件资源和并行设计特性,通过提升小波变换降低算法复杂度,减少乘法器数量,进一步利用改进的SPIHT压缩算法提高图像编码压缩质量与效率。从硬件实现结构解决了软件在处理图像压缩上的局限性,对医学领域中图像压缩处理具有一定的研究价值及参考意义。
2 医学图像压缩基础
医学图像压缩的目的是在保证临床医生诊断的前提下减少原始图像冗余,以尽可能少的数据比特表征尽可能多的诊断信息。医学图像在利用小波压缩时是将图像数据进行小波变换,实现数据由空间域变换到小波域,然后再对变换后的小波系数进行编码压缩处理。医学影像检查时由于受检者的活动、呼吸等造成的干扰信息较多,因此常常需要对医学图像进行滤波预处理[15~16]。利用小波变换对医学图像进行噪声滤除既保证了原始图像的质量又减少了图像间的冗余信息。以离散余弦变换为核心的JPEG标准因其方块效应在医学图像压缩领域不能得到很好的应用。而JPEG2000标准中所采用的离散小波变换是面积固定形状可变的有限波,支持有损压缩和无损压缩,其优良的时频特性可对原始信息在时间和频率上进行局部化分析。
3 提升小波变换及其改进
3.1 提升小波变换
经典小波变换是在傅里叶变换的基础上发展起来,其算法复杂且内存占用率大。1996 年,Sweldens 提出不依赖于傅里叶变换的小波提升方法[17](lifting scheme),通过分解、预测、更新三个步骤使原始图像分解为不同频率的子带,整个过程不需要外扩存储空间,可节约存储单元。JPEG2000静态图像标准中的两种提升小波变换方法:整数5/3 提升小波和实数9/7 提升小波。这类小波是B 样条正交小波基的一种,与Haar、Daubechies、Symlets等小波基最大的不同是它的非对称性,即分解滤波器和重构滤波器的长度不同,但其思想同biorNr.Nd小波基一样,是双正交小波对Mallat算法[18]的一种使用。小波变换分解的级数越多其分辨率越低,每一级小波变换都将待变换的图像数据进行行变换和列变换,分解为HH、LH、HL、LL 四个子带,分别表示对角线、垂直、水平方向的高频分量和低频分量,如图1所示。

图1 离散小波变换的频率分解图
3.2 5/3整数提升小波变换
提升小波变换算法由分裂、预测和更新来得到表征图像细节的高频分量和近似图像的低频分量。对于医学图像,其图像信息的准确性至关重要。5/3整数提升小波变换算法的优势之一在于它的整数提升,即忽略归一化因子的情况下,在提升步骤中将取整算子[x+1/2]作用于预测算子P(1/2)和更新算子U(1/4),从而得到小波变换的整数提升算法,使得原始图像数据精确重构。其硬件实现框图如图2 所示,其中圆圈代表加法器、减法器、乘法器,方框代表延迟器和提升算子的系数值,算法过程由式[12](1)、(2)、(3)表示如下。

图2 提升算法硬件实现结构图
分裂:

预测:
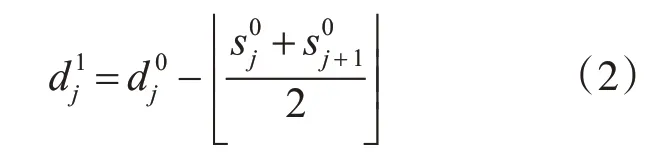
更新:

式中,xj是给定的一维输入信号,分别是信号xj经过经过高通和低通滤波且通过亚采样后的信号。
事实上小波变换要求图像是无限长的输入序列,而图像数据是有限长度的行与列,为避免图像边缘失真在进行图像小波变换时先对像素进行边沿扩展。图像数据延拓方法主要有周期延拓、对称延拓、零延拓、重复延拓和光滑延拓等。JPEG2000标准中对边界数据采用周期性的对称延拓,本文综合考虑医学图像的保真度和硬件实现条件,采用边缘不易失真且无需大量缓存器保存边界值的对称延拓法来处理边界数据。其修改后提升小波算法的预测和更新过程如式(4)、(5)所示。
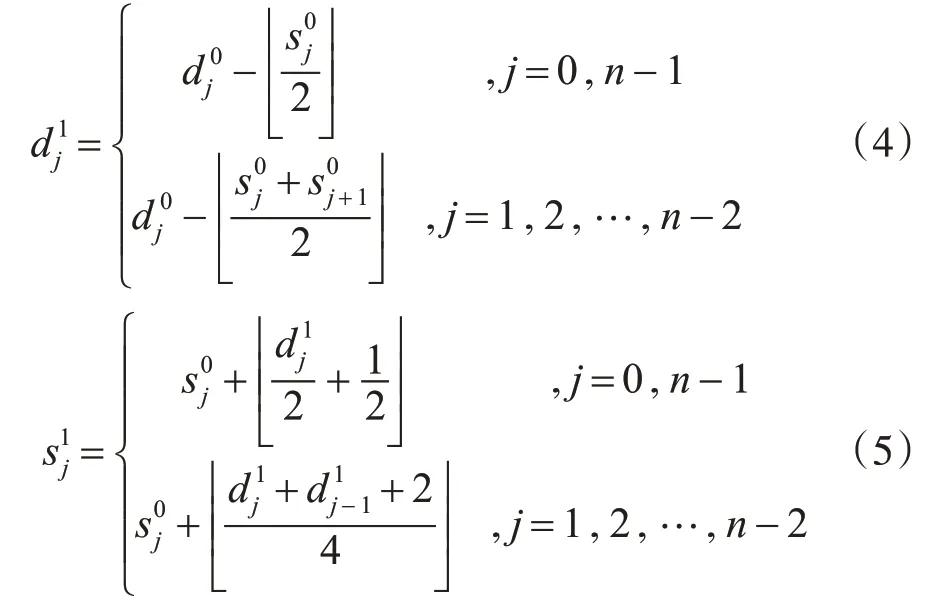
由以上公式算法可知在5/3提升小波变换中主要涉及加法及减法运算,其中少量的除法运算,通过硬件中的移位运算右移一位或者两位即可实现。此外利用小波变换的局域性,通过FPGA 资源的并行流水设计,实现图像行列变换同时进行。在图像读取完成后只需延迟几个缓存周期即可处理完整幅图像的三级小波变换,大大缩短了图像编码压缩的时间周期。同时利用FPGA 可实现变换模块与编码压缩模块的并行处理,使图像编码压缩的整个过程更高效。FPGA对上述算法的实现框图如图3 所示,经过三次2D-DWT 的流水线设计可使后续的编码模块从缓存中读取变换后的小波系数进行后续图像的编码压缩处理。
4 SPIHT压缩算法及改进方案
4.1 SPIHT算法分析
多级树集合分裂(Set Partitioning in Hierarchical Trees,SPIHT)算法相比嵌入式零树小波(Embedded Zero Wavelet,EZW)和优化截取内嵌码块编码(Embedded Block Coding with Optimized Truncation,EBCOT)节省了大量硬件资源和内存单元,具有很好的渐进传输特性。另外,SPIHT 算法的复杂度较低,峰值信噪比较高,是FPGA 系统实现医学图像编码压缩的较好选择。SPIHT 编码结合EBCOT 的位平面编码与EZW 的嵌入式编码,采用空间方向树有效表示小波系数,其树结构如图4 所示。

图3 基于FPGA的三级5/3整数提升小波变换算法框图
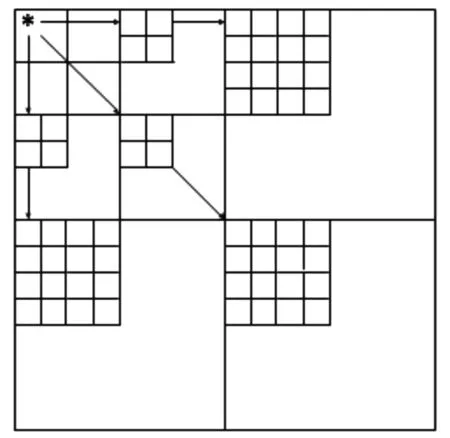
图4 SPIHT编码算法的树结构
SPIHT 算法[19]主要步骤由重要性测试、三个链表、四个集合作为算法基础,通过初始化、排序扫描、精细扫描来完成。其相关理论基础如下:
1)重要性测试。对于N 级小波变换,SPIHT 算法通过一系列阈值T0,T1,…,TN-1来确定小波系数的重要性。假设小波系数的坐标集为X={(i,j)},对于阈值T=2n中指数n 为正整数,且其中| c(i,j) |代表小波变换后系数的绝对值。对于某个小波系数或某个集合的重要性通过如下公式[19]来判别:

当Cn(X)=1 时,就称集合X 关于阈值2n是重要的;否则,称其在本级重要性测试中是不重要的。
2)三个链表。SPIHT 算法中引入三个有序表来存储系数值的坐标位置,分别是:重要系数表(LSP)、不重要系数表(LIP)、不重要子集表(LIP),带类型(D型,L型)。
3)四种集合。
O(i,j):节点(i,j)直接孩子的集合;
D(i,j):节点(i,j)直接孩子及子孙的集合;
L(i,j):节点(i,j)间接孩子即非直系子孙的集合,且L(i,j)=D(i,j)-O(i,j);
H(i,j):树根的坐标集(对应N 级小波变换,H为LLN、LHN、HLN、HHN)。
其算法步骤主要如下:
1)阈值和有序表的初始化。根据小波变换后的系数确定初始阈值,定义

2)排序扫描。按EZW 零树的Mortan 扫描顺序依次检查LIP 中的所有小波系数,判定其重要性,然后再顺次处理LIS 中的每个表项,并对D 型和L型分别处理。
3)精细扫描。给出2)中扫描时重要系数在当前位平面中的修改值。
4)进行下一次排序扫描和精细扫描。SPIHT算法在完成1 次排序扫描和精细扫描后,将输出阈值、排序扫描位流、精细扫描位流及3 个有序表的初始化信息给解码器。同时将阈值和3 个有序表的当前状态值用于下一次扫描的信息。
4.2 SPIHT压缩改进
图像经过三级5/3整数提升小波变换后被分解为高频和低频各个子带系数矩阵,对高频小波系数进行阈值优化。在此基础上利用SPIHT 算法编码时对不同子带根据实际情况进行不同深度的编码精炼次数。对LL低频近似子带采用更多的精炼次数获取高质量重构图像,而对HH 高频细节部分适当减少精炼次数甚至不编码以此提高图像压缩比。其具体压缩过程如图5所示。
5 实验结果与分析
实验将每像素8 比特,512×512 大小的医学图像首先经5/3 整数提升小波变换三级分解,如图6所示,再将变换后的小波系数使用改进的SPIHT算法编码,通过Matlab仿真验证算法。
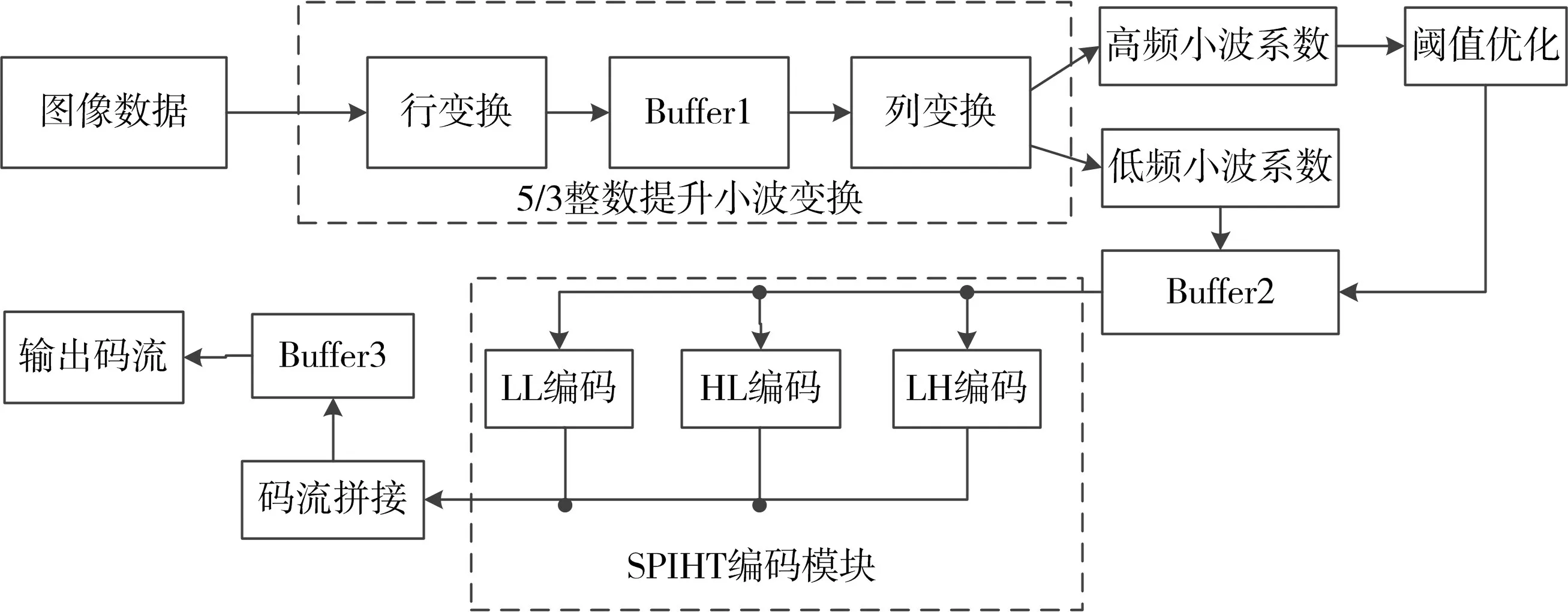
图5 改进的SPIHT编码压缩框图

图6 三级5/3整数提升小波变换
采用经过格式转换处理的5 张医学CT 图像和标准Lena 图像作为实验测试对象,利用图像保真度准则中的客观评价参数压缩比(CR)和峰值信噪比(PSNR)、重构误差方差(MSE)来评估图像压缩性能及重构图像与原图像的失真程度[20],如表1 所示。若图像大小为M*N,f(x,y)表示原图,fˆ(x,y)为解码重构图像,其MSE 被定义为原始图像与重建图像的均方误差如式(7)所示;峰值信噪比被定义为原始图像信号方差与重构误差方差之比如式(8)所示,其中K 为原始图像像素值的动态范围,对于本实验每像素8 比特的图像,K=28-1;压缩比是压缩前后表征图像的比特数之比,如式(9)所示。

通过表1 可知在5/3 整数提升小波变换的基础上采用图像各个子带进行SPIHT编码压缩的方法,相较于整幅图像一起编码执行时间更快,压缩比更高且峰值信噪比相比JPEG2000 算法几乎没有损失,解码重构图像较为清晰(如图7 所示)能够满足医学图像的诊断效果。
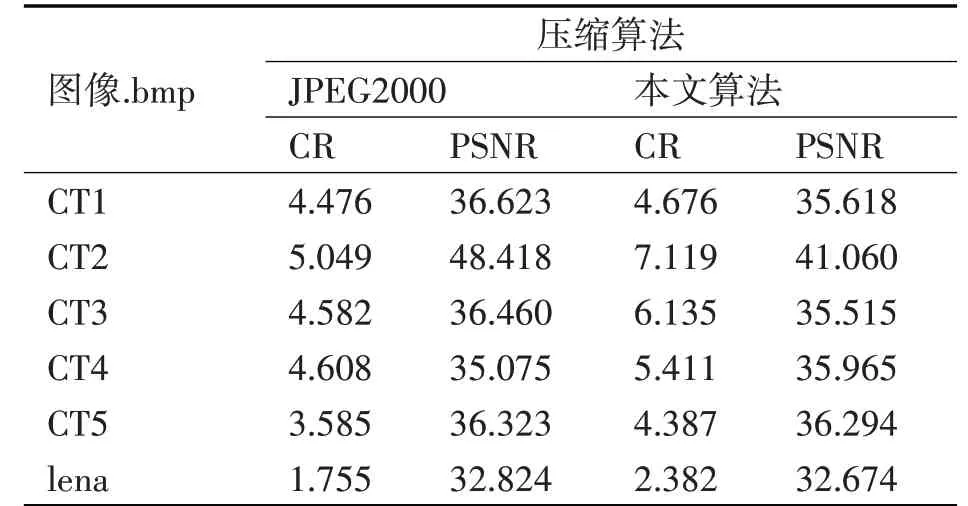
表1 压缩算法的性能评估参数

图7 医学图像压缩前后对比图
6 结语
文中通过采用双正交5/3整数提升小波变换获取到较好且适用于硬件实现的小波系数后,再采用改进的多级树集合分裂编码算法对小波系数进行编码压缩,从而实现对DICOM 医学图像格式文件的压缩处理。实验证明提升小波变换通过硬件思想优化算法,降低算法复杂度,适用于FPGA 资源并行流水的设计,可提高图像编码压缩的执行效率且保证了图像重构精度;通过对各个频率子带的阈值优化及不同深度的精炼实现医学图像的高质量压缩。以上工作可进一步从FPGA硬件系统实现角度实现图像的高效压缩,是提高压缩算法性能的较好研究方向,具有相对实用的价值,可一定程度上缓解医院PACS系统中图像数据的存储和传输负荷。

