数字图像相关法中散斑图的质量评价∗

冯益春 沈子华 朱媛媛

（上海师范大学信息与机电工程学院 上海 200000）

1 引言

数字图像相关法［1～4］是一种非接触式光学测量技术。它通过搜索目标区域变形后的位置来计算目标区域的位移场。该方法要求被测物体的表面具有随机分布的散斑，这些散斑就是物体变形的载体，会随着物体的变形而变化，因此通过检测散斑点的运动可以获取物体的变形信息。

目前可以人工制作随机分布的散斑，制作方法通常是在物体表面喷洒黑白油漆。而自然界中有些材料的表面也具有天然的散斑。这些散斑各不相同，它们的直方图分布、平均灰度等也完全不同。

散斑质量跟数字图像相关法的测量精度有着密切的关系，因此研究人员提出了众多的评价参数对散斑质量进行评估。潘兵［5］等提出了局部参数即灰度梯度平方和这一参数来评价图像子区的散斑质量，并验证了灰度梯度平方和越大，则位移测量的标准差越小。之后潘兵［6］等又提出了平均灰度梯度这一全局参数来评价散斑质量，经过验证，优质的散斑图应该具有较大的平均灰度梯度。Sun和Pang［7］提出了图像子集熵的概念，如果图像子集熵越大，那图像所包含的信息量越大。Hua［8］等人基于图像子集熵提出平均子集波动这一个全局评价参数对散斑质量进行评价。刘小勇［9］则通过引入信息论中香农熵的概念来评价散斑图像的质量。除了定量评价散斑质量的参数外，法国科学研究中心的计量小组［10］研究了图像不同的编码类型对数字图像相关测量精度的影响，他们经过实验验证，发现数字图像相关法（DIC）的测量精度会随着图像比特数的增加而增加，比特数越高，图像包含的信息量越大，散斑图像所包含的特征越多。G.Crammond［11］等采用形态学对散斑图像子集中散斑的半径大小与密度之间的关系进行了研究，验证散斑的半径大小对位移的精度有很大的影响。Lecompte［12］等、Zhou［13］等和王志勇［14］等也以散斑颗粒的大小为参数对散斑图像的质量进行了相关研究。

本文通过灰度共生矩阵提取散斑图中的能量、对比度、相关性和熵这四个特征参数，并用实验验证这四个参数对散斑质量的影响，证明了其有效性；再以平均灰度梯度作为散斑质量评价的基础参数，结合能量、对比度、相关性和熵这四个特征参数，一同作为神经网络的输入参数，训练出分类模型，利用分类模型来评估散斑的质量。

2 散斑质量评价特征参数

2.1 平均灰度梯度

合适有用的评价参数对于散斑质量的评估至关重要。平均灰度梯度的概念由潘兵［5］等提出，它是一个全局参数，其公式为

潘兵［5］等发现并验证，平均灰度梯度越大，表示散斑图像的质量越好。在一定程度上表示灰度的对比越明显，也更有利于通过数字图像相关法进行子区的搜索。

2.2 灰度共生矩阵

在平均灰度梯度的基础之上，为了更好地评价散斑质量，通过统计灰度共生矩阵中的能量、对比度、相关性和熵这四个参数，并对这四个参数进行了有效性验证。

灰度共生矩阵（GLCM）是20 世纪70 年代初由R.Haralick［15］等提出的，它通过计算图像中一定距离和一定方向的两点灰度之间的相关性，来反映图像在方向、间隔、变化幅度及快慢上的综合信息，能充分反映图像的纹理信息。

灰度共生矩阵可通过计算图像中特定距离和特定方向上两像素灰度的相关性，反映出图像在方向、间隔、变化幅度的综合信息。一般在图像处理中，图像灰度等级为256，而256的灰度等级计算量较大，也会导致灰度共生矩阵过大，因此在计算灰度共生矩阵时，将灰度等级降低至16 级，在保证效果的同时也提升了计算速度。

基于灰度共生矩阵可计算出14 种统计量。经过分析得出多个无关联参数的组合可较为准确地判断散斑质量。因此本文选取了能量、对比度、相关性和熵这四个参数作为散斑质量评价的参数。

1）能量：

式中E 表示图像的能量，i，j 表示16 级的灰度，p表示灰度共生矩阵，能量表示灰度共生矩阵元素值的平方和，可以表明图像中灰度分布均匀的程度和纹理粗细程度。如果灰度共生矩阵中元素分布较为集中，能量值会偏大。能量值越大表明分布越均匀、纹理越规则。

2）对比度：

式中C 表示图像的对比度，反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深，其对比度越大，视觉效果越清晰；反之，对比度小，则沟纹浅，效果模糊。灰度共生矩阵中远离对角线的元素值越大，对比度越大。

3）相关性：

式中R 表示图像的相关性，其中μx,μy为均值，σx,σy为标准差。相关性是指灰度共生矩阵元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时，相关值就大；相反，如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理，则水平方向矩阵的相关性大于其余矩阵的相关性。

4）熵：

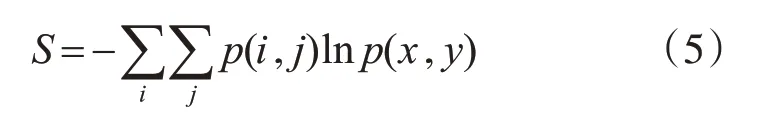
式中S 表示图像的熵，是对图像所具有的信息量的度量，它表示了图像中纹理的非均匀程度或复杂程度。

3 散斑质量评价参数的有效性验证

平均灰度梯度对散斑质量的影响已由潘兵［5］等验证，即平均灰度越大，散斑质量越好。本文通过模拟实验来验证基于灰度共生矩阵得出的能量、对比度、相关性和熵这四个参数与散斑质量的关系，即验证能量、对比度、相关性和熵对位移标准差测量结果的影响，若能量、对比度、相关性和熵对位移的标准差影响较小，则可判定这四个参数不能用于对散斑质量的评价。

实验中我们需要对图像位移的标准差进行测量，第一步是通过最小平方距离函数确认出图像变形后的位置；第二步统计目标子区图像中每个像素点变形前后的位移差；第三步求出目标子区平均位移与预设位移的差值

最小平方距离函数为

式中f(Xij)为参考散斑图像，g(δij)为经过平移后的散斑图像，是像素点Xij平移后的位置，为测出来的位移。

均值误差为

本次模拟实验目的在于验证能量值、对比度、相关性和熵对均值误差的影响，实验中排除了图像采集、光照、子区大小以及非理想加载等条件对位移测量结果的影响。实验共进行了50 组，本文只对其中一组散斑实验进行分析。图1 中的四幅散斑图来自于实验一，散斑图A、B、C 通过试件表面随机喷涂黑白漆而产生的图像，散斑图D为随机点涂材料薄膜而产生的图像。利用上述公式求得四幅散斑图对应的能量值、对比度、相关性和熵，具体数值见表1。

图1 实验所需的散斑图A、B、C、D

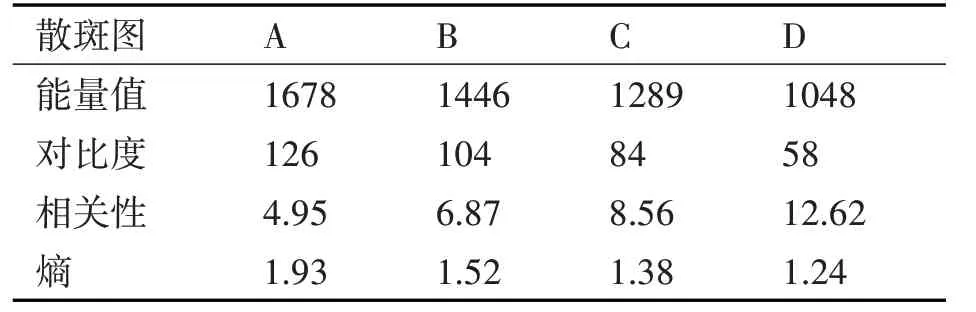
表1 实验所用四幅散斑图的能量、对比度、相关性和熵

在模拟实验中，将图一的各幅散斑图连续平移20 次的图像作为变形后数字图像，相邻两幅散斑图的间距为0.05pixel，最大的平移距离为1pixel。再利用最小平方距离相关函数计算这些平移后的散斑图像中60×60 均匀分布的像素点的位移，最后计算这些像素点位移的均值误差。

图2、图3、图4 以及图5 显示的是四幅散斑图平移量0～1pixel 时，60×60pixel 的图像子区位移的均值误差。结果表明对于不同的散斑图，均值误差的大小也不同，结合表1，可以发现，当散斑图的能量越大，对比度越大，相关性越小，熵越大，位移的均值误差越小即散斑质量越好，所以以上四个参数可作为评价散斑质量评价的有效参数。

图2 散斑图A平移1pixel后的位移均值误差

经过上述实验的验证，可以得出能量、对比度、相关性和熵对散斑图像的质量有一定的影响。结合已论证的平均灰度梯度，因此本文选取了能量、对比度、相关性、熵以及平均灰度梯度作为散斑质量评估的参数。

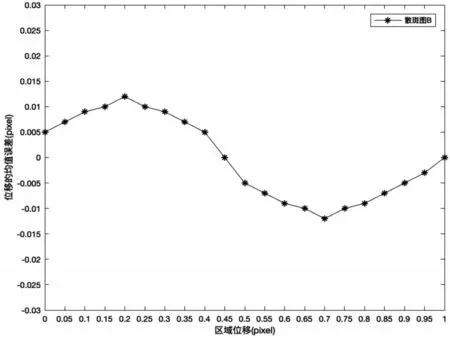
图3 散斑图B平移1pixel后的位移均值误差

图4 散斑图C平移1pixel后的位移均值误差

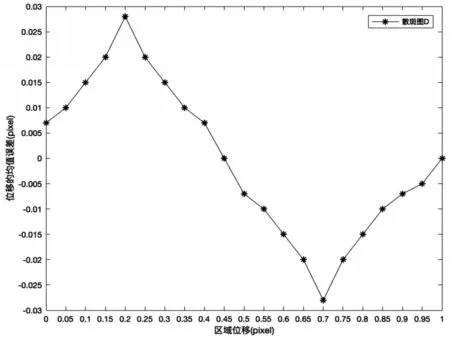
图5 散斑图D平移1pixel后的位移均值误差

4 散斑质量的实验结果与分析

本文基于灰度共生矩阵提取了能量值、对比度、相关性和熵四个参数，结合平均灰度梯度，将以上五个参数作为输入向量，通过神经网络训练出分类模型，最终输出散斑的质量评价。

实验中模拟了实际场景对散斑的影响条件，如光照、随机度等，图6 和图7 分别是实验装置图，和示例散斑图。本次实验共采集了优质和劣质的散斑图各200张，这200张散斑图作为训练集，同时准备了质量好和质量差的散斑图各50 张，用作效果验证。

图6 实验装置

图7 示例散斑

为了得到较为准确的分类模型，使用了不同组合的参数进行训练，方案A表示能量、对比度、相关性和熵的组合；方案B 表示能量、对比度、相关性、熵和平均灰度梯度的组合；两种方案的结果如表2所示。

表2 A、B两种方案的正确率对比

表2 明显看出B 方案的正确率有大幅增长，也表明了平均灰度梯度这一参数相比其余参数更具备明显的特征，所以通过B 方案的参数组合，可以得到较为准确的分类模型，对散斑质量进行优劣的分类。

5 结语

本文首先通过灰度共生矩阵提取散斑图中的能量、对比度、相关性和熵这四个特征参数，并用实验验证这四个参数对散斑质量的影响，证明了其有效性；为了较为准确地评价散斑图像的质量，以平均灰度梯度作为散斑质量评价的基础参数，结合能量、对比度、相关性和熵这四个特征参数，一同作为神经网络的输入参数，通过神经网络训练后，得到较为准确的二分类模型，进而实现散斑图像的质量评价。结果表明，在参数有效的条件下，利用感知器的分类能力，可以得到较为准确的散斑质量评价。