基于集成CW-RNN 的时间序列预测研究∗

刘 絮 郑建国

（东华大学 上海 200051）

1 引言

时间序列目前的分析方法可以分为两类：基于统计学的时间序列分析和基于数据驱动的时间序列挖掘。基于统计学的时间序列分析方法是比较早期的研究方向，主要思想是将整个时间序列看做为一个整体，采用统计的方法构建一个全局的模型。基于数据驱动的时间序列挖掘方法是着重于提取数据的序列关系，不需要满足统计学中的某些前提假设。

基于数据驱动的时间序列挖掘方法中，机器学习训练模型过程中最需要解决两个问题：参数可以学习到当前数据和历史数据之间的关系；训练出来的模型有较强的泛化能力。其中，循环神经网络（RNN）的隐藏层内神经元之间互相连接，隐藏层内上一次迭代的输出为下一次迭代的输入，使其适用于处理有短期序列相关的数据。但是，在使用随机梯度下降学习模型参数时，多次迭代中参数容易出现梯度消失，这就使得距当前时间点较远的历史信息很难被网络捕捉到。该问题的改进方法有长短期记忆网络（LSTM）［1］、使用二阶梯度优化，例如Hessian Free（HF）［2］、在一阶梯度优化训练过程中加入动量并恰当地设计初始化果［3］、Clockwork RNN（CW-RNN）［4］等。

单独来源的数据训练的模型具有局限性，当对预测需要考虑更多与其相关的变量时，可采用分析模型中的向量自回归（VAR）。并使用集成算法将多个来源的数据模型结果融合，使模型包含更多信息，提高其泛化能力。在集成算法中，stacking集成算法可以融合不同类模型，并实证其在预测准确度上较其他算法更加优秀［5～6］。

基于以上，本文提出一种适用于多维度时间序列的预测模型。采用stacking 算法，将CW-RNN 提取的时间序列自回归信息，与VAR 拟合的相关变量信息融合。本文的主要贡献是：将CW-RNN 模型用于时间序列预测问题，提高自回归的预测准确度，并使用stacking集成算法融合多个模型结果，有效提高泛化能力，使预测的整体准确度更高。

2 CW-RNN结构简述

2.1 前向传播过程

Clock-work Recurrent Neural Network（CWRNN）是一种循环神经网络，其结构包含输入层、隐藏层和输出层。独特之处为隐藏层的神经元之间并不是标准RNN 的全连接。而隐藏层神经元被分成了g 个模块，每一个模块中有hn∈{h1,…,hg}个神经元，并且每个模块有不同的驱动间隔Tn∈{T1,…,Tg}。在每一个模块内部，kn个神经元之间是全连接，但是在不同模块之间的神经元的连接只是从驱动间隔大的模块到驱动间隔小的模块。将模块按照驱动间隔从小到大，从左往右的顺序排列，可以得到只有一层隐藏层的CW-RNN 结构如图1所示。

图1 一层隐藏层的CW-RNN结构示意图

CW-RNN 的正向传播计算和标准RNN 相似，只是增加了时间t 对隐藏层信息传递的影响。在CW-RNN 中，输入层权重矩阵WI，和隐藏层权重矩阵WH都被分成了g 行，每一行分别对应一个模块。

其中，WO为输出层的权重矩阵，bO是输出层的偏差，fO(·)为输出层神经元的激活函数，为隐藏层在时刻t的输出，其计算公式为

其中输入层权重矩阵WI和隐藏层权重矩阵WH都被分成了g 行，见式（1）。 x(t)为在t 时刻的输入，bH是隐藏层的偏差，和分别是隐藏神经元在t 时刻和t-1 时刻的状态值，同时也是输出层的输入，见式（2）。

CW-RNN 的隐藏神经元与标准RNN 相比不同点在于：1）CW-RNN 隐藏层模块之间的连接只存在于大时间间隔模块到小时间间隔模块之间，所以隐藏层权重WH就是一个上三角矩阵，WHi可以表示为

2）在不同时刻t 隐藏层内激活的神经元不同，在t 时刻时只有满足时间驱动间隔Ti∈{T1,…,Tg}可以被t整除（t mod Ti=0）的模块才有输出。在实际计算式（3）时，只有与可以激活的模块相对应的WH和WI会使用。即可将权重WH看做为分段函数：

CW-RNN 独特的隐藏层结构使其既能存贮长期记忆，又能捕捉到高频信息。时间驱动间隔较大模块的权重更新次数较少，能存储距运行时刻t 较远的信息。并且模块之间的连接只是从驱动间隔较大的模块到间隔较小的模块，所以间隔较大的模块的权重参数不会受到频繁输入数据的影响，可以较好地保存长期信息。时间驱动间隔较小模块的输入不仅包括输入层传递的新数据，还包括了较大时间间隔隐藏层模块的输出，等于接收到高频序列关系信息。CW-RNN 的最终输出共同取决于所有隐藏层神经元，可以将所有长期和短期信息都考虑在内。

在训练CW-RNN的参数时，与标准RNN相似，参数学习算法是Backpropagation through time（BPTT）［7］。对于CW-RNN 来说，其反向传播仅作用于在时刻t 激活的模块。和前向传播相似，未激活的模块依旧使用t-1 时刻的值，且其权重不会更新。

2.2 CW-RNN相关算法

本部分将简单概述RNN 相关的模型配置和算法理论，其中包括参数学习算法和参数初始化方法，为后文的实验提供理论支持。

2.2.1 常用的梯度优化方法

1）随机梯度下降（SGD）在更新梯度时引入了动量［9］，通过负梯度和上一时刻权重更新值vt-1的线性组合来更新当前的参数θt，C 为整体的损失，定义见式（6），该方法参数更新Δθt的公式为

其中，ϵ 为学习率，α 为上一时刻梯度的权重，表示之前的梯度对当前时刻梯度下降方向的影［3］。动量的作用是尽量排除掉异常数据对梯度方向的误导。

2）适应性梯度算法（AdaGrad）中学习率依据累计平方梯度，独立适应所有模型参数。其更新过程如下：

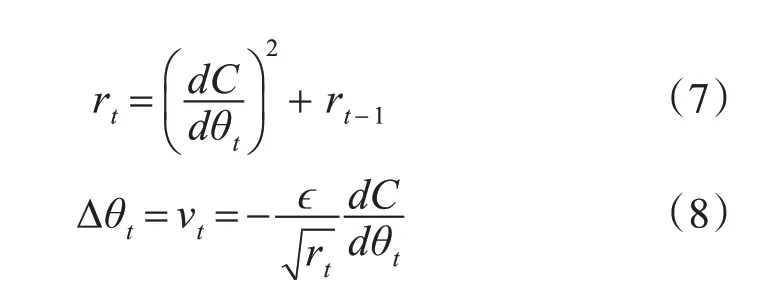
其中，ϵ 为学习率，一开始较大，用于快速梯度下降。随着优化过程的进行，对于已经下降很多梯度的参数或者有较小偏导的参数，减小学习率；对于还没怎么下降的参数或者是具有较大偏导的参数，保持一个较大的学习率。这就可以根据式（7）中的rt来衡量该参数梯度历史下降的程度。故该方法适用于稀疏样本的问题，即每次梯度下降的方向和涉及的参数会存在较大的差异［9］，或者说在参数空间中更为平缓的倾斜方向效果会更好［10］。

3）均方根传播（RMSprop）对式（7）中的rt的更新增加了一个衰减系数γ 控制历史梯度对学习率的影响比重，即将梯度累计改为指数加权的移动平均。

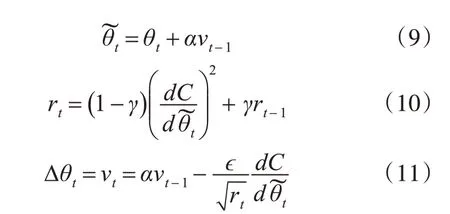
其中，ϵ 为学习率，γ 为衰减系数，用于控制移动平均的长度范围。RMSprop 中式（10）使学习率衰减的幅度依赖于当前梯度和历史梯度的大小。动量结合了自动调节学习率和梯度方向，RMSprop 具有较强的鲁棒性，能够很好的处理随机问题［11］。

4）适应性矩估计（Adam）通过计算梯度的一阶矩估计和二阶矩估计，为不同的参数设置独立的自适应学习率。

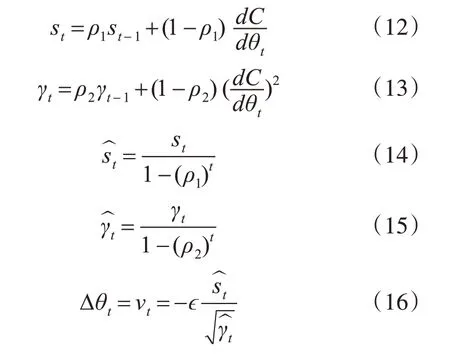
其中，ϵ 为学习率，式（12）和式（13）计算了梯度的指数移动均值st和平方梯度γt，并且ρ1和ρ2表示矩估计的指数衰减速率。此时为了抵消初始化的偏差，使用式（14）和式（15）对偏差进行修正，得到偏差修正的估计和［12］。Adam 算法的计算比较高效，可以较快地收敛，对超参数的选择有较强的鲁棒性。

2.2.2 网络权重初始化算法

在深度学习过程中，权重初始化的设置对模型收敛速度和学习的效果有十分重要的影响。目前比较常用的权重初始化的方法有标准初始化和Xavier初始化。标准初始化使得有n个节点的神经网络的初始化权重W满足均匀分布为

使用深层的神经网络，随机数初始化一旦随机分布选择不当，会导致参数很难被更新［13］。

Xavier 初始化方法的基本思想是保持输入和输出的方差一致，可以有效地避免梯度消失，使得信息可以持续的传递。在有n 个节点的网络中，初始化权重W满足均匀分布：

Xavier 初始化权重系数后，正向传播的激活函数值和反向传播的梯度值明显比标准初始化的要稳定，网络训练会更快，更容易收敛到局部最优。

3 集成CW-RNN模型

本文中的集成CW-RNN 模型分为三部分：CW-RNN 自回归部分、VAR 模型部分和stacking 集成部分。将神经网络灵活的预测能力和时间序列统计模型严谨的态度相结合，并用集成方法将两者的预测结果组合，尝试具有更强泛化能力的预测方法。

3.1 自回归部分

CW-RNN为时间序列因变量Y的自回归，可根据Y 的客观特征设定其滞后阶数，并保证滞后阶数为输入层的神经元个数。CW-RNN 的模型复杂度依据数据量和模型训练的拟合度进行调整。

在本文中，CW-RNN的激活函数使用tanh［4，13］。并在权重初始化时，尝试使用标准初始化和Xaiver初始化［14］。理论上隐藏层每一个模块内神经元的个数可以任意，但方便起见，模块内使用相同的神经元个数。第i个模块的驱动间隔采用Ti=2i-1［4］。在参数训练过程中实验使用较为稳定的RMSprop算法和Adam算法［12］。

3.2 相关变量回归部分

为了将因变量Y 预测值中考虑到与其相关的自变量X 的影响，本文引入VAR 模型。在变量数大于样本数的情况下，可采用偏最小二乘估计对模型的参数进行估计。VAR 模型的的一般数学表达式为

式中，Y 为内生变量，取p 阶滞后项，X 为外生变量，取r 阶滞后项。 A1…Ap和B1…Br为待估计的参数。 εt为随机干扰项，不与自身滞后项和式（19）中等号右边的变量相关［14］。

为了得到平稳的时间序列，将时间序列差分直到可通过ADF 单位根检验。并使用格兰杰因果检验为平稳时间序列选择滞后阶数［15］。

传统标准化方法通常是全局标准化，即利用全局范围的数据的最大值xmax和最小值xmin对数据做约束：

但是因为时间序列相邻时刻之间存在相关性，且在时间维度上数据是不断产生的，如果要使用式（20）来进行标准化，在较长的且有趋势的时间序列上不利于不同时段数据的比较。在此基础上，引用信号处理中归一化的方法［16］，结合傅里叶变换中加窗的思想，对于时间序列的归一化可采用加窗归一化。将时间序列S 加窗分成长度为L 的n 段窗口，si∈{s1,…,sn} 。归一化公式为

归一化后得到的序列为R={r1,…,rn} 。该归一化时考虑了相邻时间序列的相关性，由参数α 和β 控制。

3.3 stacking集成

集成学习是将许多模型的预测结果，以不同的方式组合起来，共同决定最终结果的方法。集成学习方法主要有stacking、bagging和boosting。后两者均是通过随机和重采样的方法组合多个同一种模型，stacking 是一种可以将多个不同类的模型组合起来的方法，且已被证实效果要好于其他两种集成方式［5］。本文将把CW-RNN 和VAR 模型的预测结果通过stacking的方法，采用线性函数，将两者的预测结果组合起来，并得到最终的预测结果。

4 某上市公司股票成交价实证分析

本文的研究目的是检验预测模型的效果，根据时间序列数据的可获得性，选取某上市公司的股票成交均价作为因变量，取该上市公司的资产负债信息和宏观经济指标作为自变量。VAR 部分采用季度成交价，CW-RNN采用每日成交价，stacking部分将自回归结果转化成季度后，再集成VAR 模型得到最后的季度预测价格。

数据依据时间维度被划分为三部分，其中前1/2 部分用于CW-RNN 和VAR 两个初级学习器的参数训练；中间1/4 部分作为初级学习器的验证数据集，并用于生成集成用于训练stacking 集成次级学习器部分的训练数据集；最后1/4 部分用于验证次级学习器的泛化效果。数据这样设置是为了减少整体模型产生过拟合的风险，且较为全面地反映模型的整体效果。

4.1 自回归部分

时间序列的自回归部分将先对CW-RNN 的训练方法进行调整与比较，再将其与相同配置的LSTM 和标准RNN 进行比较，衡量标准为均方根误差（RMSE）。

根据式（17）的标准初始化和式（18）的Xavier初始化方法，同时与参数学习算法RMSprop 和Adam 进行比较，实验10 次的均方误差的均值和标准差如表1 所示。此处以及本文之后的预测均为向前一步预测，暂不考虑向前多步的预测问题。

表1 CW-RNN模型初始化方法和参数学习算法RMSE比较

通过假设检验的方法对算法的显著性进行判断。在使用Adam 算法和标准初始化的效果更好，故下文将使用标准初始化和Adam 算法进行CW-RNN的参数学习。

本文将CW-RNN 与标准RNN 和LSTM 网络这两种循环神经网络相比较，此处三个模型都使用完全相同的超参数：隐藏层神经元为tanh、1层隐藏层神经元、隐藏层神经元个数为160 个、参数训练使用Adam 算法、参数标准初始化等。实验10 次的对比结果如表2所示。

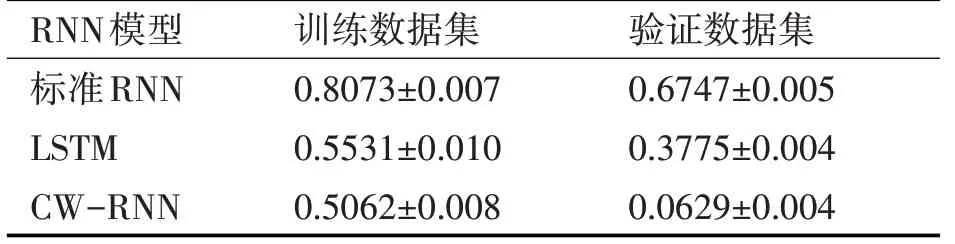
表2 CW-RNN模型与标准RNN和LSTM的RMSE比较

CW-RNN 与 标 准RNN 相 比，CW-RNN 与LSTM和标准相比，有较好的泛化能力，更适用于预测回归的问题。故在该时间序列场景下，使用CW-RNN 的效果更好，后续本文将使用该CW-RNN作为集成学习的初级学习器之一。

4.2 stacking部分

此部分将CW-RNN和VAR模型两个初级学习器集成在一起，集成stacking 方法采用线性回归。训练数据集采用CW-RNN和VAR模型验证数据集生成的数据。集成后的模型和单独的初级学习器比较结果如表3所示。

表3 集成模型的RMSE比较

集成CW-RNN 比单独CW-RNN 和单独VAR模型的效果要好。特别是在验证数据集上，集成模型的RMSE比单独CW-RNN要低了大约41%，说明集成多维数据的模型可以提高泛化能力，更适合于处理预测问题。

5 结语

本文通过stacking 集成算法，融合CW-RNN 和VAR 模型。并利用某上市公司股票的成交均价作为算例，对时间序列的回归和预测做了实证检验，并可以得出结论：1）CW-RNN 可以较好地用于时间序列问题的预测上，优于标准RNN 和LSTM。2）用stacking集成方法也有助于提高回归预测的准确度，优于单独的CW-RNN 和单独的VAR。该模型适用于多维度的时间序列预测情况，且可以有效提高准确度，具有很强的实用价值。