发展数学抽象能力 提升学科核心素养
杨秀丽
(福州第十一中学,福建福州 350001)
一、问题的提出
《普通高中数学课程标准(2017 年版)》将数学抽象确定为数学学科的核心素养之一。教师对数学抽象的重要性是认同的,但在实际教学中存在以下两个问题:教师教学方法传统单一,只注重结果,缺乏经历得到完整概念的教学抽象过程;对数学抽象的认识不到位,不知道可以从哪些方面入手培养学生的数学抽象。那么,如何认识数学抽象?在教学过程中,可以从哪些方面具体地落实数学抽象的培养呢?
二、对数学抽象的认识
(一)数学抽象的内涵
数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程。主要包括:从数量与数量关系、图形与图形关系中抽象出的一般规律和结构,并且用数学语言予以表征。[1]数学抽象具体有两个维度:一个维度是数量关系,[2]例如,从1 个人,1 个苹果,1 根木棒中抽象出数字“1”,从形状、大小不同的三角形中抽象出“三角形内角和等于180°”;另一个维度是图形与图形的关系,[2]例如,从现实生活中抽象出三角形、四边形、圆等图形的概念,从形状、大小不同的等腰三角形中抽象出“三线合一”的性质。
(二)数学抽象的价值
史宁中教授将数学的基本思想归结为三个,数学抽象就是其中之一。不仅如此,数学抽象还被认为是理性思维的基础、数学的本质特征,它贯穿于数学学习的整个过程。从过程来看,通过抽象,我们从具体情境中得到数学的概念、性质、模型等;从结果来看,在获得知识的过程中同时还积累了数学抽象的经验,发展了数学素养。由此来看,数学抽象既具有学科价值,又充分体现了教育价值。
三、教学过程中对数学抽象的培养
《普通高中数学课程标准(2017 版)》指出,数学抽象主要有以下四个方面的表现:获得数学概念和规则,提出数学命题和模型,形成数学方法和思想,形成数学结构和体系。无论是新知学习还是复习巩固,数学抽象都蕴含其中,教学过程中可以从以下这几个方面培养、发展学生的数学抽象。
(一)学会抽象数学问题的共性并获得概念
数学抽象能力作为数学最基本的思想,它将数学中所包含的数学概念、数学定理、数学公式加以概括,用抽象的形式加以呈现给学习者,使得一类共同的问题得出普遍性的结论。[1]数学抽象是形成数学概念的重要途径,数学概念的形成就是对数学问题进行抽象化概括的过程。所有的数学概念都是通过抽象获得的,有的是从现实世界中直接抽象出来的,有的则是在数学内部,对已有知识进一步抽象而成的。例如,在函数概念的教学时,我们提供以下几个情境:
1.汽车以60km/h 的速度匀速行驶,行驶路程为skm,行驶时间为th。
2.某景区门票的售价为30 元/张,一天售出m 张门票,门票收入为n 元。
3.圆形水波中,圆的半径为rcm,圆的面积为Scm2。
4.用10m 长的绳子围一个矩形,矩形的一边长为xcm,它的邻边为ycm。
虽然这些情境反映了不同事物的变化过程,但它们都涉及两个变量,而且这两个变量之间都具有一种共同的属性,即当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应。现实生活中还存在很多这样的例子,于是,我们从这些具体的情境中抽象出“函数”的概念,随着学习的深入,在函数概念的基础上,我们又进一步抽象出正比例函数、一次函数、二次函数、反比例函数等概念。在具体的情境中获得数学概念,可以经历概念的“抽象化”和“数学化”。
(二)能抽象问题规律,提炼命题,建立数学模型
命题学习是数学学习的一个重要环节,而数学命题也是通过抽象、推理提炼出来的。例如,前面所说的正比例函数,在抽象出概念之后,我们先分别画出函数y=2x,y=x,y=-1.5x,y=-4x的图象,再思考以下几个问题:
1.从“数”的角度看,这4 个函数的自变量x的取值范围是否相同?y 的取值范围呢?
2.从“形”的角度看,这4 个函数的图象是否存在共同或不同之处?
3.你认为函数y=0.3x与上述4 个函数中的哪个(或哪几个)在图象上具有相同的特征?能否写出一些与函数y=-1.5x在图象上具有相同特征的函数;(这里的特征是指2 中所得到的共同之处)
4.能否从这些具体的例子中归纳出一般性的结论,并用数学语言表述。
通过上述问题的思考,我们得出正比例函数y=kx(k 是常数,k≠0)的图象是一条经过原点的直线。当k>0 时,直线y=kx 经过第一、第三象限,y 随x 的增大而增大;当k<0 时,直线y=kx 经过第二、第四象限,y 随x 的增大而减小。
在正比例函数图象及其性质的学习中,我们经历由具体到抽象、由图形语言和自然语言到符号语言表达的过程,并在此过程中发展数学抽象的素养。
除命题外,我们还将现实世界或数学内部在数量关系或空间形式上一些带有普遍性的规律抽象出来,并用数学的形式或结构予以表示,这就形成了数学模型。例如,三角函数模型、指对数函数模型等。
由于命题和模型具有一定的“工具性”,所以从某种意义上来讲,命题和模型的抽象要难于概念的抽象,对抽象素养的培养也更具发展性。
(三)认清问题本质,抽象数学思想方法
数学思想是在人们对数学知识的认识过程中逐步形成的,它存在但“无形”,这些思想方法来源于知识的认识过程并运用于后续的认识活动中。在数学命题和模型的抽象过程中往往蕴含着数学的思想方法。例如,在上面所提到的正比例函数性质的学习过程中,通过“数”和“形”两个角度研究正比例函数,由此抽象出“数形结合”的思想;根据k 的符号,对正比例函数y=kx的性质进行分类提炼,由此抽象出“分类讨论”的思想。这些思想方法在后续的一次函数、二次函数、反比例函数的学习中不断运用。再如,平面向量的教学可以类比物理中矢量教学,将未知的问题化归为已知问题,用类比方法学习,抽象出“化归”的思想。由于数学思想方法的“无形”,所以它更显得高度抽象。
(四)能把相关数学知识抽象形成知识体系
数学抽象的更高水平体现在对相关数学知识抽象形成知识体系。我们按照章节进行新知识的学习,虽然每一个章节相对独立,但实际上不同章节之间的知识存在着联系,能抽象出不同章节知识之间的联系并建立知识体系,是学好数学的有效方法,更是发展数学抽象的重要途径。笔者开过一堂《方程的根与函数的零点》公开课,上课前先让学生讨论:一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图像有什么关系?要求学生完成以下表格。(如表1)

表1
学生观察讨论容易得出方程的实数根就是函数图象与x 轴交点的横坐标。方程的根是从“数”的角度研究问题,而函数图像与x 轴交点是从“形”的角度研究问题,正体现了数形结合思想。教师进一步给出函数零点概念。学生归纳等价关系:方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点。这种等价关系,为我们分析问题解决问题提供了函数与方程的数学思想方法。让学生从已知的知识抽象出未知知识,辨别它们之间的联系,使知识结构体系更完整,提高学生数学抽象的能力。
四、数学抽象在解题活动中的运用
在学习过程中,通过符号、概念、命题、模型等学习以及思想方法的提炼,我们的数学抽象素养得以逐步地发展,再将这种素养运用于解题以及后继的学习中,下面以一道例题简单说明数学抽象在解题中的运用。(如图1)

图1
由于实际背景对学生来说陌生,数据繁杂,学生感到困难,教师应当引导学生分析题中数据,教会学生如何将实际问题抽象为恰当的数学模型。
活动:问题1:观察上表的数据,你发现了什么规律?问题2:根据数据作出散点图,观察图形,你认为可以用怎样的函数模型刻画其中的规律?(如图2)
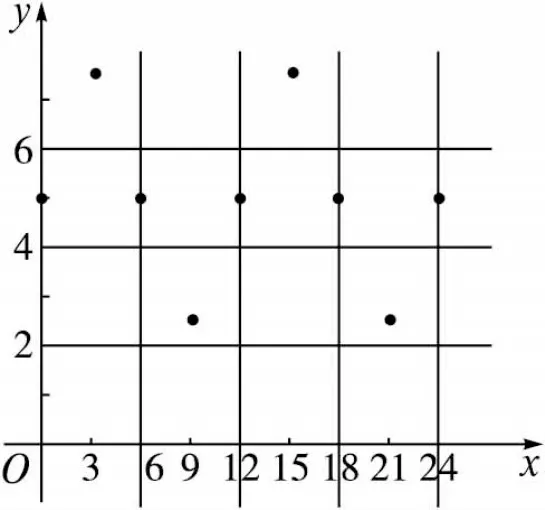
图2
教师引导学生根据散点的位置排列,从实际问题中发现周期变化的规律,根据散点图中的最高点、最低点和平衡点,引导学生将所发现的规律抽象为三角函数模型。港口的水深与时间的关系可以用形如y=Asin(ωx+φ)+h 的函数来刻画。再将实际问题抽象为数学符号来表示,其中x是时间,y 是水深,我们可以根据数据确定相应的A,ω,φ,h 的值即可。这时注意引导学生与“五点法”相联系。教师指导点拨,并纠正可能出现的错误,直至无误地求出解析式,进而根据所得的函数模型,求出整点时的水深。教师有必要准备丰富的教学素材,帮助学生体验从实际背景中“抽象数学问题—构建数学模型—寻求数学方法—解决实际问题”的过程。[3]
在本题的解题过程中,蕴含了函数与方程、建立数学模型等重要的数学思想方法,如前所述,这些思想方法正是在长期的学习过程中不断抽象出来的,运用这些思想方法就是对数学抽象结果的升华。
数学抽象可以让学生更好领会数学本质,提高数学思维能力,通过抽象问题本质,教会学生自主学习,独立思考,达到培养学生核心素养的目的。这就需要我们在教学过程中引导学生用心感悟,慢慢体会,并通过运用使其得以发展,最终形成自身的一种素养。

