基于HMM的电动汽车行车轨迹纠偏优化

刘伟东，赵 新，李 磊，刘小琛，李 丹

(1.国网天津市电力公司 电力科学研究院，天津 300021；2.国网天津市电力公司 营销部，天津 300010)

0 引 言

由于电动汽车广泛应用的基础设施如充电设施较少，限制了电动汽车的进一步发展。电动汽车行车轨迹数据可应用在电动汽车充电设施的整体规划中，精确的电动汽车行车轨迹数据可以结合城市规划及交通情况，为充电设备选址规划提供数据支撑[1-4]。特别是在无人驾驶电动汽车领域，精确的轨迹能够确保无人驾驶汽车的高安全性[5-7]。行车轨迹的经纬度等定位数据信息变化频繁，其可以结合GPS、电子地图和可视化等技术进行轨迹绘制和定位的特点，从而可以将汽车行驶过程中不符合道路特征的定位数据信息进行纠偏，以正确获得行车轨迹，进而获得更为准确的定位数据，解决轨迹不准确等问题。现有文献提出了基于数据拟合、概率统计和预测等方法以解决轨迹不准确问题，但还是存在定位频率低引起定位轨迹信息不连续等问题。隐马尔可夫模型(hidden Markov model，HMM)是一种统计模型，当前已有研究将其与物联网技术集成应用在轨迹预测中[8-10]。本文将采用HMM模型进行电动汽车的行车过程中定位轨迹的数据不准确问题进行纠错，并提出了隐马尔可夫纠偏定位点优化算法以提升定位精度，可为电动汽车的充电设施的选址提供精确的行车轨迹数据来源。

1 相关理论

隐马尔可夫模型是一种关于时间序列的概率模型，是经典的预测模型。其中的马尔可夫链概念是指在给定已知信息和状态的情况下，只使用当前信息去预测未知的信息，已知的信息称为可见状态链，未知的状态称为隐马尔可夫链。其应用在预测方面，仅使用当前已知的状态去预测未来的未知状态，隐马尔可夫模型的具体定义请参见文献[10]，此处简述本文用到的部分相关概念及定义如下

P(Xn+1=x|X0,X1,X2,…,Xn)=P(Xn+1|Xn)

(1)

式中：Xn代表当前的状态，Xn+1代表在已知当前状态的情况下Xn+1的状态。Xn+1和Xn有关，与X0,X1,X2,…,Xn-1无关，这种假设性前提则是一阶马尔可夫链；如果未来状态只与前两个状态有关，那么称为二阶马尔可夫链；……，以此类推。

隐马尔可夫模型用能观察到的马尔可夫可见状态链去预测隐马尔可夫链。针对车辆轨迹的纠偏问题，原理上属于预测问题，可用隐马尔可夫模型，即在已知监测位置信息的情况下来预测实际的行车轨迹位置信息，将偏离实际位置较大的定位数据进行剔除。

假设K为所有可见状态链的状态集合，G是所有可观测到的状态集合

K={q1,q2,…,qM},G={g1,g2,…,gN}

(2)

I为长度是t的状态序列，O是对应观测序列

I={i1,i2,…,it},O={o1,o2,…,ot}

(3)

设状态数为N，观测数为M，隐马尔可夫模型(λ)通常用λ=(A,B,π) 表示。其中，A是状态转移概率矩阵，B是观测概率矩阵，π是初始状态概率向量，具体如下

A=[aij]M*M

(4)

式中：aij=P(it+1=qj|it=qi), 1≤i,j≤M。

B=[bj(k)]M*N

(5)

式中：bj(k)=P(ot=gk|it=qj), 1≤k≤N, 1≤j≤M。

π=(πi)

(6)

式中：πi=P(i1=qi), 1≤i≤M。

2 行车轨迹纠偏模型

建立的基于隐马尔可夫的行车轨迹模型主要包括如下部分：

(1)可见状态链：从待定位车辆的定位感知设备(例如GPS定位终端、手机位置传感器等)中获取电动汽车所在位置的经纬度。

(2)观测序列：Y=(Yx|x=1,2,…,S)， 其中S代表有定位设备在S个位置处采集到的经纬度定位数据信息。如图1所示，黑色实心点A、B、C、D为观测序列。

图1 行车轨迹模型中的相关序列

(3)交通道路路网节点：RN=(P,R)， 其中P=(pi|i=1,2,…,m) 表示道路上的结点，比如交叉路口、道路起点等，R=(rj|j=1,2,…,n) 代表轨迹中路网上的各条道路。如图1所示，白色空心点P1～P6等为交通道路中的路网节点；图1中各路网节点所在的道路即为路网上的各条道路rj。

(4)隐藏序列：Z=(zi|i=1,2,…,t)， 车辆所处真实位置，即为需要预测与纠偏的真实行车轨迹定位序列。

下面分别介绍该模型中的观测概率、状态转移概率和初始状态概率。

(7)

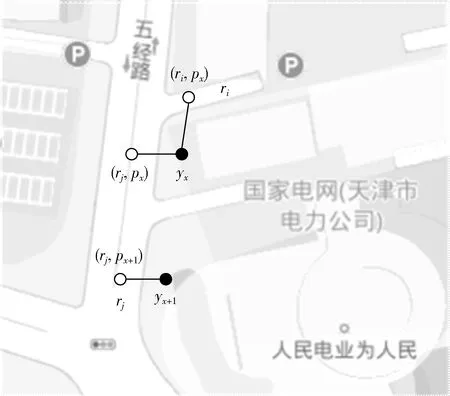
图2 车辆轨迹观测概率

(2)状态转移概率：与候选定位点之间的真实距离成正比，表示如下

p(px+1=zj|px=zi)∝e-α dij

(8)

式中：dij表示候选定位点zi与zj之间的距离，α是影响zi与zj之间最短距离元素的参数。

(3)初始状态概率：p(y1|p1=z1)。

在时间t状态为i的所有路径 (i1,i2,…,it) 中概率最大的值是

δt(i)=maxP(it=i,it-1,…,i1,ot,ot-1,…,o1)
i=1,2,…,M

(9)

由此可推导得出δ

δt+1(i)=maxP(it+1=i,it,it-1,…,i1,ot+1,ot,…,o1|λ)=
max[δt(j)aji]bi(ot+1)
i=1,2,…,M;t=1,2,…,T-1; 1≤j≤M

(10)

那么在时间t状态i的所有路径中概率最大的第t-1个结点为

Ψt(i)=argmax[δt-1(j)aji]i=1,2,…,M

(11)

在此模型中，通过计算与位置点的距离来决定隐藏状态点，应用Viterbi算法求解隐藏状态点的观测概率。

3 隐马尔可夫纠偏定位点优化算法

由于HMM模型存在如下两种假设：①齐次马尔可夫假设；②观测独立性假设。齐次马尔可夫指的是隐马尔可夫链任意时刻的状态只与它前一时刻的状态有关；观测独立性指的是任意时刻的监测只依赖于该隐马尔可夫链的状态。在所构建的轨迹纠偏模型中，由于GPS信号、设备故障或网络信号等原因导致的观测到的定位位置出现偏差，这会导致采用传统的基于HMM的行车轨迹纠偏方法的偏差相应增大。所以本文在应用隐马尔可夫纠偏模型之前使用遗传算法先对定位点进行优化，剔除偏差较大轨迹点，从而提升轨迹纠偏模型的准确率。具体如算法1所示：

算法1：隐马尔可夫纠偏定位点优化算法

输入：道路节点定位位置序列(P1、P2、……)

输出：删除偏移点后的优化权重W

步骤1 将行车轨迹中的第一个定位点作为权重点，设置权重点α值以及距离阈值D，进入步骤2。

步骤2 根据定位点和唯一权重点生成定位轨迹，进入步骤3。

步骤3 轨迹生成过程中，在出现定位偏差较大的定位点时，权重点根据公式W′=α*Pi+β*Pi-1进行更新(其中，α+β=1)，W′代表更新后的权重点。若此后的若干定位点没有偏移，则判定这个定位点有效，加入轨迹中并且更新权重点，进入步骤4；否则，判定为偏移点并删除，进入步骤5。

步骤4 输出权重W′。

步骤5 输出权重W。

下面结合图3、图4和图5分别针对行车轨迹中存在的起始点偏移、中间点丢失和单个偏移点等常见情况进行说明。假设选取权重初始值w(0≤w≤1)， 下一个权重点更新为W2=P1*(1-w)+P2*w。

(1)起始点偏移

如图3所示，假设实心黑色点为定位设备监测到的定位点，空心白色点为权重点。如果定位点P1、P2与P3之间的距离超过了设定的正常距离阈值，则可能P1与P2发生了偏移，这时需要为P3重新生成权重点W2；通过判断后面连续的点之间是否有偏差来判定前述的点偏移情况，如果没有异常则这些点的轨迹正常。如果判定P1和P2发生了偏移，则删除P1和P2点。

图3 行车轨迹中起点偏移

(2)中间因为某些原因失去定位点

如图4所示，GPS定位设备本身、汽车供电设备电路故障等其它原因导致行车轨迹中间部分没有定位信息，但是除去这部分后分开的两部分行车轨迹都是正常的情况。

图4 行车轨迹中丢失部分中间定位信息

图5 行车轨迹中存在单个偏移点

(3)有单个偏移点

如图5所示，首先算法检测出定位轨迹中偏移点P4，则更新权重点为W2；接着检测出偏移点P5，则删除W2；然后在接下来的轨迹如果没有偏移点，则更新权重点为W1，并且判定P4点为单个偏移点进行删除。

4 实验与性能分析

本文的实验平台通过开发的Java程序调用百度地图API获取定位车辆的行车轨迹原始GPS定位数据。实验过程中选择了天津市国家电网天津市电力公司附近区域的路段，进行了20次的行车轨迹记录实验。在实验数据预处理阶段，将路段根据行车道路分段进行数据预处理，分段删除偏移点。经过对每段收集原始经纬度信息与提出的基于HMM的行车轨迹纠偏优化模型在准确度方面进行了对比，具体实验相关参数配置和实验结果见下面的分析。

4.1 实验参数设置

具体的实验参数见表1。在实验中设定初始权值w为0.8，w值越大表示更新权重点越接近最新定位点，主要是考虑到实际行车过程中，权重点的选择更应该与后续定位点之间的距离越近，更符合实际的行车轨迹特征。阈值距离D的选取主要是根据行车过程中的平均时速来给定。

表1 参数设置

4.2 实验结果分析

图6展示了轨迹数据与处理前与处理后定位准确度的对比，因为经过预处理后删除了偏移点，行车轨迹的定位准确率得到了较好的提升。

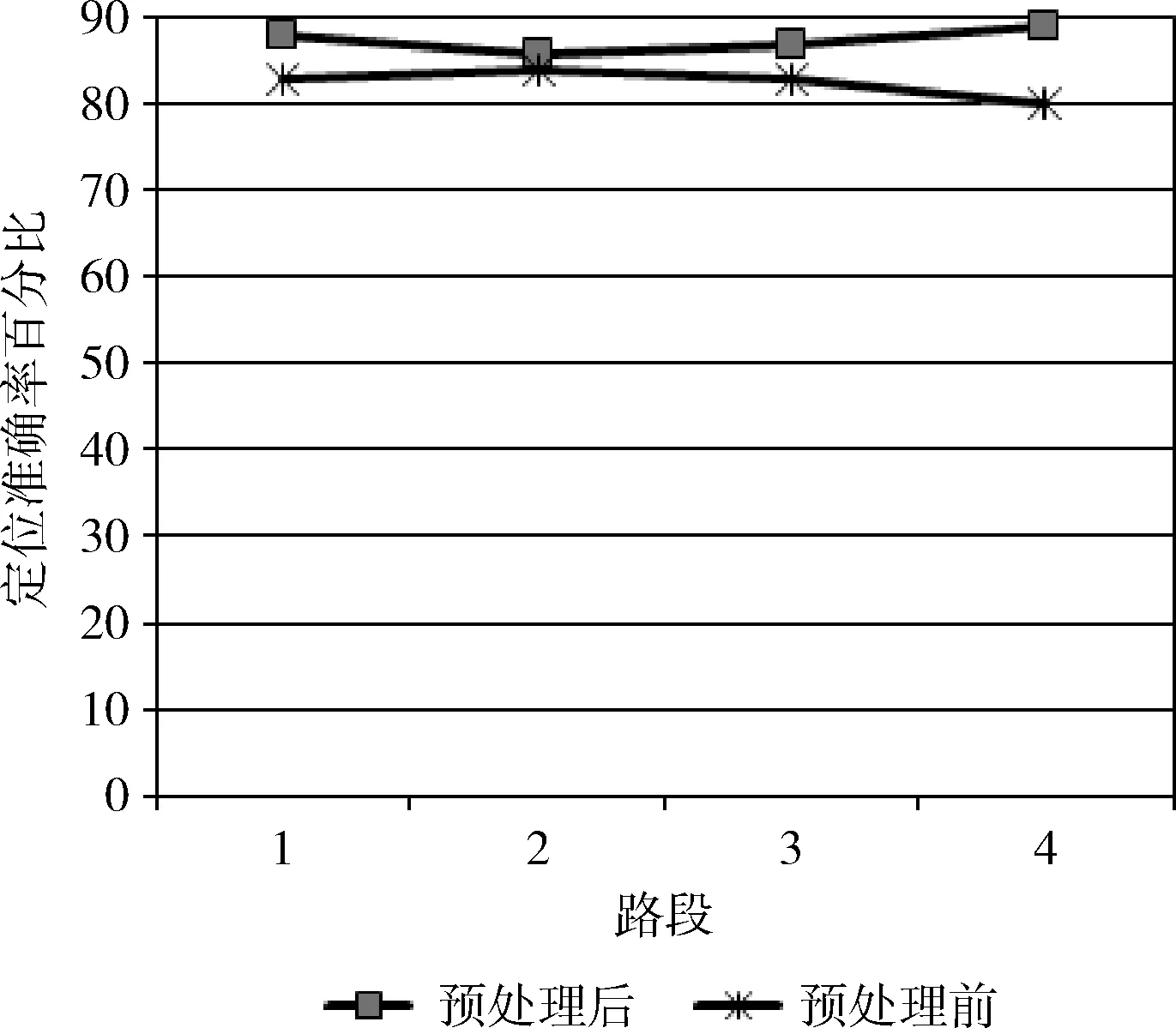
图6 轨迹数据预处理前后定位准确率对比

图7 轨迹数据预处理后使用隐马尔可夫纠偏模型前后定位准确度对比

由图7可以看出，与没有使用纠偏算法进行数据预处理的隐马尔可夫模型相比，经过轨迹预处理之后使用隐马尔可夫模型的轨迹纠偏方法在不同的路段其准确率均率均达到90%及以上，实验结果表明本文方法的可行性和鲁棒性。

5 结束语

本文研究提出了一种行车轨迹纠偏优化方法，该方法结合电子地图并采用隐马尔可夫模型和Viterbi算法对预处理过后的行车轨迹进行纠偏，建立了轨迹纠偏模型，通过使用遗传算法先对原始定位点进行优化，以剔除偏差较大的异常行车数据。实验结果表明本文提出的基于HMM的行车轨迹纠偏优化方法能够提高电动汽车的行车轨迹准确性，并提升了其轨迹数据的应用价值。该方法可以为电动汽车的充电桩位置选址提供科学的数据依据，并能够给自动驾驶提供精确的定位信息并提高自动驾驶行车路径的采集信息准确度。由于当前算法仅在单机环境中进行算法和性能测试，未来考虑构建云平台环境下的纠偏优化算法应用系统。