基于双重目标的树枝形专用线取送车优化
李 冰,张志宁
(郑州大学 管理工程学院,河南 郑州 450001)
0 引 言
树枝形专用线是铁路枢纽内常见的一种铁路联络线布置形式,其特点是小运转列车连挂本地车组到达装卸站并完成取送作业后可直接前往下一装卸站而不必返回编组站,树枝形专用线取送车作业中,各装卸站货车入线时刻不同,但取回编组站内时刻相同[1]。
近些年来,关于树枝形专用线取送车优化方面,李斌等[2]以货车总消耗时间最小化为优化目标,同时提出遗传蚁群算法求解该问题。温旭红等[3]提出了具有树状结构的铁路车流径路优化模型,设计拉格朗日松弛算法求解模型。郭垂江[4]以成本多目标为优化模型,并设计模拟退火算法对模型进行求解。赵娟[5]以车流总走行车公里最小为目标,建立线性0-1规划模型。张文晰等[6]针对路企直通列车组织过程中车流整列到发的取送问题,研究了装卸区呈树枝形布置成组装卸情形的取送方案。郭垂江等[7]把取送车作业优化问题转换成哈密尔顿图最短路问题,采用匈牙利算法进行求解。程磊等[8]以调机总走行时间最小为优化目标,提出了一种改进蚁群算法求解该问题。
针对多目标模型优化问题,相关文献研究主要利用智能算法进行求解。汤兆平等[9]针对多目标规划模型设计了基于TOPSIS方法和限定参数区间搜索的模型求解方法。陈希琼等[10]构建了最小化总行驶距离和最小化不同车辆行驶距离最大差以平衡各车辆的工作负荷的双目标模型,并提出一种多目标蚁群算法。Aringhieri等[11]提出了基于邻域搜索的启发式算法解决多目标问题。葛显龙等[12]设计了结合聚类分析和扫描算法的混合遗传算法解决带时间窗的路径优化问题。Mirakhorli等[13]设计了多目标线性规划方法解决物流网络优化问题。Adamo等[14]研究了带时间窗约束的货物取送径路和速度优化问题,构建了问题模型并给出了分支定界求解算法。Haddad等[15]研究了货物分批取送问题,并设计了一个局部搜索启发式算法。
就目前查阅的文献来看,关于树枝形专用线取送车优化方面主要集中在调机取送成本和周转时间的单目标优化,考虑多目标优化的文献较为欠缺,此外较多文献没有考虑时间窗要求。因此,基于以上文献研究,本文围绕服务铁路枢纽地方货物流的小运转作业系统,研究一类带时间窗的树枝形专用线取送车优化问题(optimization of placing-in and taking-out wagons on branch-shaped siding with time window,OPTWBS-TW),组建基于调运成本最小与货车总周转时间最小的双目标数学规划模型,提出了遗传算法和模拟退火算法(genetic algorithm & simulated annealing, GA&SA)融合求解策略,最后进行实验验证与数值分析。
1 问题描述与研究条件
1.1 问题描述
本文所研究的OPTWBS-TW问题可以描述为:在铁路枢纽树枝形网络N={i|i=0,1,…,A} 中,其中i=0 时表示编组站,i≠0时表示装卸站,非直达列车陆续到达编组站,枢纽内编组站对到达列车解体和出发列车编组,完成“列流转变为车流”和“车流转变为列流”,装卸站对货物进行装车和卸车工作,完成“货流转变为车流”和“车流转变为货流”。考虑各装卸站i的作业要求和时间窗限制,一台调机往返编组站和装卸站之间对所有作业进行取送工作。本文基于既考虑取送作业成本又考虑加速货车周转,建立了调运成本最小和周转时间最小的双目标数学模型,其中调运成本分为调机走行成本、货车走行成本和调机早到或晚到成本;周转时间为调机将阶段时间内所有货车从编组站送往装卸站至作业完成后取回编组站的总完成时间。
1.2 研究条件
针对OPTWBS-TW问题,考虑如下研究条件:
(1)单调机作业,调机最大牵引定数和最大走行时间已知;
(2)树枝形专用线网络中编组站、装卸站间的机车走行时间已知;
(3)装卸站待送货车、待取货车已知;
(4)装卸站作业时间窗要求已知,即特定装卸站有固定作业时间窗,调机在规定时间外到达装卸站,会因装卸站设备占用、整备等原因产生调机早到等待成本和调机晚到惩罚成本,即额外成本。
(5)调机在固定作业时间窗之前到达装卸站,则调机等待至作业时间开始;调机在固定作业时间窗之后到达装卸站,则直接开始工作。
(6)随同一列车到达编组站,且目的装卸站一致的货车编为同一车组。车组取、送两种作业独立核算。
(7)不考虑货车取送编组站后连挂列车。
2 模型构建
2.1 符号约定
为构建模型,引入以下参数与变量:
(1)输入参量
N:铁路枢纽内装卸站集合,记为N={i|i=0,1,…,A}, 其中i=0时表示编组站,i≠0时表示装卸站,A为铁路枢纽内的装卸站总数。
t(i,j):装卸站i到装卸站j的走行时间,其中i或j=0表示编组站到装卸站的走行时间,i,j∈N。
cl:调机单位分钟运营成本。
cw:货车单位分钟运营成本。
P:调机最大牵引定数。
D:调机最大行驶时间。
L:陆续到达铁路枢纽的货物列车序号集合,记为L={l|l=1,…,B}。 其中B为到达的货物列车总数。
l(i):随货物列车L到达铁路枢纽且目的装卸站为i的本地作业车组,l∈L,i∈N。
Ml(i):车组l(i)的货车编组数,l∈L,i∈N。
Tl(i):本地作业车组l(i)在目的装卸站i处完成装卸作业所需的时间,l∈L,i∈N。
Z:作业性质集合,记为Z={z|z=1,2}, 其中z=1表示送车作业,z=2表示取车作业。
U:取送作业编号集合,记为U={u=l(i)z|i∈N,l∈L,z∈Z}。l(i)1表示将车组l(i)送往装卸站i的送车作业;l(i)2表示将车组l(i)由装卸站i取回编组站的取车作业。
[ETi,LTi]:表示装卸站i允许的作业时间窗。ETi和LTi分别为装卸站的最早作业时刻和最晚作业时刻,l∈L,i∈N。
K:调机取送批次集合,记为K={k|k=1,…,R}, 其中R为取送批次总数。
(2)状态变量
ol(i): 本地作业车组l(i)到达编组站后到解完成时刻,l∈L,i∈N。

tl(i): 车组l(i)到达目的装卸站i处送车时刻,l∈L,i∈N。

πk: 调机第k批次从编组站出发时刻,k∈K。

w(i,j): 调机从装卸站i到装卸站j所牵引的货车数量,其中i或j=0表示编组站到装卸站或装卸站到编组站所牵引的货车数量,i,j∈N。
αl(i): 装卸站i的等待成本。调机在最早作业时刻ETi前到达装卸站i,所产生的等待成本。记为αl(i)=e1(ETi-tl(i)), 其中e1为单位分钟等待成本,i∈N。
βl(i): 装卸站i的惩罚成本。调机在最晚作业时刻LTi后到达装卸站i所产生的惩罚成本。记βl(i)=e2(tl(i)-LTi), 其中e2为单位分钟惩罚成本,i∈N。
(3)决策变量
S(i,j): 0-1参数,表示调机是否由装卸站i驶向装卸站j,如果调机途径(i,j),则S(i,j)=1, 否则S(i,j)=0,其中i或j=0表示编组站,i,j∈N。
T:总周转时间,即完成取送作业编号顺序解ψ(l(i)z) 所需的总时间,i∈N,l∈L,z∈Z。
2.2 模型构建
基于以上表述,以总调运成本最小化和货车总周转时间最小化为双重目标,考虑时间窗要求,构建问题模型。
(1)调运成本最小化目标,由3部分构成,即调机走行成本、货车走行成本和调机早到或晚到成本

(1)
(2)货车总周转时间最小化目标,以加速货车周转。货车总周转时间为调机将阶段时间内所有货车从编组站送往装卸站至作业完成后取回编组站的总完成时间
minZ2=T
(2)
(3)调机最大走行时间约束,即保证调机从编组站出发至回到编组站的走行时间小于调机的最大走行时间
(3)
(4)调机牵引定数约束,即调机牵引货车数量不得超过调机牵引定数
w(i,j) (4) (5)取送作业顺序约束,即同一车组作业先送后取,且送取作业的时间间隔大于货物装卸时间 第三,区域活动场地没有得到完善。一些幼儿园为了节省成本投入,对幼儿活动场地建设以及器材的完善仅仅是流于形式。但是,在幼儿园区域活动中,活动器材以及场地都是非常重要的组成部分,直接影响到幼儿的身心发育。如果幼儿园在建设、布置的时候没有考虑到幼儿的实际需求,那么这样的区域活动条件则会严重影响区域活动开展有效性。 (5) (6)取送作业数目约束,即所有取车作业数目等于所有送车作业数目 (6) (7)变量取值约束 S(i,j)∈{0,1}, ∀i,j∈N (7) (8)货物作业时刻约束,即本地作业车组l(i)取回编组站完成时刻大于本地作业车组l(i)到达编组站后到解完成时刻 (8) 解决多目标优化问题的最终目的只能是在各个目标之间进行协调权衡,使各子目标均尽可能达到最优。本文采用理想最大值-最小值的双目标归一化处理,具体步骤如下: 步骤1 单目标下目标函数值的确定 通过计算机运行找到目标函数1的最小值Z1min、 最大值Z1max及目标函数2的最小值Z2min、最大值Z2max, 则目标函数1和目标函数2取值范围分别为[Z1minZ1max]、 [Z2minZ2max]。 步骤2 目标函数值归一化处理。 设第i条取送车径路hi对应的目标函数值1和目标函数值2分别为Z1i和Z2i,归一化处理后目标函数值1和目标函数值2分别为Z1(hi)和Z2(hi),则 (9) (10) 该问题属于NP-hard问题,利用传统求解算法较为困难,且效率不高,故采用启发式算法进行求解。考虑到遗传算法GA能够很好地解决优化排序问题,且具备运行内在隐蔽性和良好的稳定性,故采用GA算法求解该问题,但GA算法容易陷入局部最优,且易早熟。模拟退火算法SA在解决优化排序问题也有较好表现,具有更好的全局收敛性,能够很好互补GA算法的缺点,因此提出GA算法和SA算法融合求解该问题。该融合算法首先利用GA算法进入循环迭代,在每次迭代过程中,改进自适应交叉变异概率以增强算法全局寻优能力和收敛速度,最后利用SA算法进行二次迭代寻优,最终形成GA&SA融合求解算法。相对于遗传算法、蚁群算法、粒子群算法等智能算法,GA&SA求解算法融合了GA和SA的优点,同时嵌入参数自适应调整策略,能更好地改善搜索的广度和深度。GA&SA具体步骤如下。 根据铁路枢纽内装卸站集合和陆续到达铁路枢纽的货物列车序号集合,其中装卸站集合N={i|i=0,1,…,A}, 其中i=0时表示编组站,i≠0时表示装卸站,A为铁路枢纽内的装卸站总数;货物列车序号集合L={l|l=1,…,B}, 其中B为到达的货物列车总数,利用取送车径路中的作业编号构造问题的解,对于取送作业集合U,每个l(i)z表示一项取送车作业,则所有取送车作业集合的排列组合即为取送车径路的解,记为h,则取送车径路的解表示为h={ψ(h(x))|h(x)=l(i)z,i∈N,l∈L,z∈Z,l(i)z∈U,x∈1,…,S}, 其中ψ(h(x)) 表示所有取送车作业集合的排列组合,S为取送作业编号集合数。设H=[h1,…,hw]T为初始取送车径路种群规模,hw为一个取送车径路的解,w为取送车径路集合H中所涵盖的取送车径路数量。该编码方式将一个时段内的全部取送作业视为整体考虑,从而找出较优取送车径路。 4.2.1 选择操作 令f1(hi)=θ*Z1(hi)、f2(hi)=(1-θ)*Z2(hi), 其中hi为一个取送车径路的解。则适应度函数f=1/(θ*f1(hi)+(1-θ)*f2(hi)), 那么每个取送车径路个体被选择的概率为Pi=f/∑f, 根据轮盘赌规则,随机生成一个位于[0 1]的随机数rand,并与随机数rand进行比较从而确定选择范围。 4.2.2 交叉操作 为扩大解的搜索范围,采用PBX交叉。具体过程如下: 步骤1 从上一代取送车径路规模群体中随机选择一对父代取送车径路个体h1和h2; 步骤2 选择父代取送车径路个体h1和h2若干个基因,位置可不连续,但选择一对父代取送车径路个体的基因位置必须相同; 步骤4 找出被选中的基因在另一个父代取送车径路个体的位置,在将其余基因按顺序放入生成的子代取送车径路个体中。具体过程如图1所示,其中图1(b)为生成的另一个取送车径路。 图1 PBX交叉过程 4.2.3 变异操作 设置两点变异操作如下: 步骤1 从上一代取送车径路规模群体中随机选择一个取送车径路个体h3; 步骤2 对于取送车径路个体h3,随机产生两个基因位τ1和τ2; 4.2.4 参数自适应设计 针对GA参数的确定,设计动态交叉概率Pc和动态变异概率Pm, 使其随实际环境的变化而不断变化。当个体的适应度较低时,增加交叉和变异的概率;反之,则降低交叉和变异的概率。具体设置如下 其中,fmax为种群中最大适应度值;fave为种群平均适应度值;f′为进行交叉的两个父代染色体中较大的适应度值;f为变异个体的适应度值;Pcmax和Pcmin分别为交叉概率的上界与下界,设置 [pcmin,pcmax]=[0.5,0.99], [pmmin,pmmax]=[0.1,0.5],Q为迭代次数,MQ为最大迭代数。 为进一步改善解的质量,利用SA扩大搜索范围,以找到更优解。将迭代到一定次数后的GA算法导入SA进行二次寻优,对SA每个初始解和邻域解进行评估,更新GA种群,循环往复,直至满足终止条件。 4.3.1 冷却进度表的参数确定 冷却进度表是控制SA算法进程的重要参数,包括温度控制参数T,初始温度控制参数T0,温度停止控制参数Tend,温度衰减因子,马尔科夫长度,初始马尔科夫链长度0,马尔科夫链变换因子δ,邻域解变换次数q。 4.3.2 邻域解的变换规则设计 4.3.3 邻域解的接受概率设计 SA的二次寻优更新过程具体步骤如下: 步骤1 基于GA初始取送车径路生成。对迭代到一定次数的每代GA种群选择最优取送车径路个体,记做hbest, 并计算Z1(hbest) 和Z2(hbest)。 步骤2 初始化参数。给定初始温度控制参数T0,温度停止控制参数Tend,温度衰减因子,初始马尔科夫链长度0,马尔科夫链增加因子δ。令温度控制参数T=T0,马尔科夫长度=0, 初始邻域解变换次数q=1。 步骤3 基于温度控制参数衰减终止条件判断。若T>Tend,则执行步骤4,否则转步骤7。 步骤5 邻域解变换次数控制。令q=q+1, 若q<, 则执步骤4进行邻域解变换;否则步骤6。 步骤6 温度控制参数T和马尔科夫链长度更新。令T=T×,=×δ, 更新温度控制参数T和马尔科夫链长度。 步骤7 算法终止,输出最优取送车径路hbest, 更新GA种群,从而进入下一代迭代寻优。 设计由12个装卸站组成的树枝形小运转作业网络,如图2所示。设计实验时段内有4列货物列车相继到达编组站,各列车解体后的本地作业车取送信息数据见表1。树枝形专用线网络中各装卸站及编组站间的调机走行时间数据见表2。 图2 铁路枢纽树枝形专用线 表1 铁路枢纽到达车流信息 表2 装卸站间调机走行时间/min 根据以往文献研究,对GA&SA算法的参数进行经验性设置:调机单位分钟运营成本cl=16元,货车单位分钟运营成本cw=1.2元, 单位分钟等待成本e1=2, 单位分钟惩罚成本e2=8, 调机最大牵引定数P=40, 调机最大行驶时间D=300 min; 初始温度控制参数T0=1000, 温度停止控制参数Tend=0.01, 温度衰减因子=0.9,初始马尔科夫链长度0=2000, 马尔科夫链变换因子δ=0.9, 初始邻域解变换次数q=1, 最大迭代次数Q=160, 种群规模w=200。 当本文GA算法迭代到40代以后,利用SA算法进行二次寻优,得到GA&SA算法。 为了验证算法的有效性,对所提出的GA&SA算法与本文所提的GA、SA以及蚁群算法(ant colony algorithm, ACA)进行性能对比测试,GA、SA算法参数与GA&SA算法保持一致,ACA参数设置参考文献[8],利用Matlab R2014a对GA&SA、SA、GA和ACA求解策略进行编程,在Windows 8操作系统,处理器为Intel(R) Core(TM) i5-3337U CPU(1.80 GHz) 微机上运行。对于双目标函数,本文θ分别取100%、50%、0%,从而输出双目标函数的求解质量与算法迭代次数的演进关系如图3所示,决策者可以根据实际需要,从中选择较小的调运成本或者较小的货车总周转时间,或者二者折中。 图3 不同θ值下求解质量与算法迭代次数的演进关系 从图3(a)可以看出:当θ=100%时,即决策者100%偏向目标函数1,随着迭代次数的增加,4种算法总调运成本不断下降,但总周转时间呈现上升的趋势。可以看出当决策者一味追求总调运成本最小时,求得的总周转时间较长。 从图3(b)可以看出:当θ=50%时,即决策者既考虑总调运成本,又考虑总周转时间。随着迭代次数的增加,4种算法目标函数值呈波浪式的下降。 从图3(c)可以看出:当θ=0%时,即决策者100%偏向目标函数2,随着迭代次数的增加,4种算法总周转时间不断下降,但总调运成本呈现上升的趋势。可以看出当决策者一味追求总周转时间最小时,求得的总调运成本较大。 总体来说:双目标函数不存在绝对的最优解,当决策者追求较低的总调运成本时,则总周转时间则会较长;当决策者追求较短的总周转时间时,则总调运成本则会较高。从运行结果可以看出GA&SA求解结果较好,SA求解结果较差。相对来说,SA、GA和ACA收敛较早,容易陷入局部最优,GA&SA收敛较晚,在迭代后期扩大了解的搜索范围,得到更高质量的解。故而,在嵌入参数自适应GA中引入SA明显提高了算法的性能。 为更直接观察取送车取送作业情况,表3给出了在计算时间限定条件下的GA&SA、SA和GA算法计算结果,即将GA&SA的运行时间内分别执行GA和SA,以保证相同的运行时间,从而更公平的比较运行结果。设置θ=0.1, 其它参数不变。 从表3运行结果看出:GA&SA相对于GA和SA得到了更高质量的解。GA&SA算法得到的最小周转时间为720 min,总调运成本为43 099.8元;GA算法得到的最小周转时间为736 min,总调运成本为45 600.8元;SA算法得到的最小周转时间为812 min,总调运成本为54 890.4元,由此可以说明GA&SA相对于SA和GA改善了解的质量。 表3 计算时间限定条件下的GA&SA、GA和SA算法计算结果 表3(续) 对于GA&SA运行结果,调机被划分为7个批次,第1、2批次为同送模式,第3、4、5、6批次为取送结合模式,第7批次为同取模式;对于GA运行结果,调机被划分为7个批次,第2、3批次为同送模式,第1、4、6批次为取送结合模式,第5、7批次为同取模式;对于SA运行结果,调机被划分为8个批次,第1、2、4批次为同送模式,第3、7批次为取送结合模式,第5、6、8批次为同取模式。 本文围绕铁路枢纽地方货物流,研究一类带时间窗的树枝形专用线取送车优化问题,组建了基于调运成本最小与货车总周转时间最小的双目标数学规划模型,该模型通用性强,决策者可根据问题的具体情况选择各种合理的取送作业方式。鉴于双目标模型复杂,首先对双目标模型进行基于理想最大值-最小值的归一化处理,紧接着设计了GA&SA融合求解策略。该融合求解策略首先给出基于作业编号的取送车方案表述,进而设计嵌入参数自适应策略的GA解更新过程,并设置SA算法进行二次寻优,从而找到最优取送车径路。最后设计仿真实验,对所提出的方法进行过程验证,结果表明,相对于GA、SA及ACA,融合求解策略GA&SA在解的质量方面表现更佳。3 基于理想最大值-最小值的双目标归一化处理
4 基于双目标的GA&SA混合算法
4.1 基于作业编号的取送车方案表述
4.2 嵌入参数自适应策略的GA解更新过程
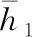



4.3 基于SA的二次寻优更新过程
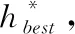



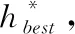


5 实验验证及结果分析
5.1 实验场景



5.2 过程验证



6 结束语
——房室结双径路参与传导的顺向型房室折返性心动过速
——房室结双径路的少见电生理表现

