基于矩阵运算的极小碰集求解方法

陈旭琳，赵相福，褚 鹏，陈中育

(浙江师范大学 数学与计算机科学学院，浙江 金华 321004)

0 引 言

随着科技的发展，各行各业的系统越来越复杂精密，传统的专家系统诊断方法已越来越难以高效应对[1]。为了适应系统规模不断扩大的现状，避免分析耗时过长等问题[2]，排除专家诊断的主观干扰因素，人们提出基于模型的诊断[3]。通常，基于模型的诊断分为冲突识别[4]和候选产生[5]两步：第一步冲突识别是对比预期行为和观测结果得到极小冲突集[6]，而后的第二步候选产生是根据已知的冲突集簇求出系统的极小碰集[7]。由Reiter所著故障诊断领域的经典论文可知，这些极小碰集是可能导致系统故障的原因，即系统的候选诊断[8]。显然，为了提高求解候选诊断的效率，必须提高求解全体极小碰集的效率[9]。本文研究在已知冲突集簇时求解极小碰集的算法。

求解极小碰集被证明是NP-hard问题[10]，众多研究人员对极小碰集算法进行全面的研究和深入的改进[11]，目前已经存在许多算法，包括HS-Tree算法、HST-Tree算法、CSSE-Tree算法、蛛网算法、CHS-Tree算法等。这些算法存在各自的优缺点和特定的适用范围，主要缺点集中体现在几个方面：需要建立树或图，缺乏明显的规律，数据结构及算法的实现较繁琐；需要进行剪枝，而剪枝过程可能会丢失正确解；用基于树结构的算法，一般均需要首先建立树，再由树经过较复杂的递归计算才能产生碰集。

本文针对上述求解极小碰集算法的缺点，提出一种基于矩阵运算求解极小碰集的方法，这种算法直接通过矩阵乘法运算求解，即将碰集求解的问题转化为矩阵的乘法运算问题。算法的主要优点是：该算法不需要建立树或图，数据结构非常简单，易于程序实现；该算法不需要进行剪枝，因而不会因剪枝而丢失正确解；该算法思路和流程相对简洁清晰；矩阵的性质保证结果的正确性；不需要将冲突集简化为极小冲突集，直接使用冲突集求解；某些情况下算法的求解效率较高。

1 预备知识

以下系统性介绍一些基于模型诊断的相关概念和基础定理。

定义1 一个系统定义为一个三元组 (SD,COMPS,OBS)， 其中：

(1)SD是系统描述，是一阶谓词公式的集合，包含诊断中的主要信息；

(2)COMPS是系统中组成部件的集合，一般用有限常量集 {c1,c2,…,cn} 表示；

(3)OBS是系统观测值的集合，是用一阶谓词公式表示的有限集合。

在待诊断的设备中，使用一元谓词AB(·)表示“abnormal”(反常)，即系统实际的行为与系统预期的行为不相同。另外，如果系统部件发生故障，但实际输出与预期输出相一致，则仍认为不是“反常”。AB(c)为真时，当且仅当c反常，其中c∈COMPS。

定义2 冲突集(CS)也称为冲突部件集，是一个部件集 {c1,c2,…,cn}⊆COMPS， 使得SD∪OBS∪{～AB(c1),～AB(c2),…,～AB(cn)} 不一致。当冲突集的任意真子集都不是冲突集时，该冲突集被称为极小冲突集(MCS)。

定义4 若集合S1和S2满足S2⊂S1， 则称S1为S2的真超集。

下面通过例1对上述概念进行说明。

例1：假设一个系统的冲突集簇F={{1,2},{1,3},{1,2,3},{1,4},{2,4}}， 包含系统部件1、2、3、4，{1}、{2}、{1,4}、{1,3,4}、{2,3,4}是该集合簇的部分候选解，其中，{1,4}、{1,3,4}和{2,3,4}是碰集，并且只有{1,4}、{2,3,4}是极小碰集。由于集合{1,3,4}为集合{1,4}的真超集，因而集合{1,3,4}不是极小碰集。

2 矩阵计算极小碰集

2.1 算法描述

下面对使用矩阵求解极小碰集的算法进行简述，算法步骤如下：

步骤1 将冲突集簇以某种转换规则转换为矩阵A。

集合与矩阵转换规则1规定如下：定义m×n参数矩阵，其中m为冲突集合簇中包含冲突集的个数，n为冲突集合簇中包含系统部件的个数。矩阵中第i行第j列的值aij表示第i个冲突集是否包含第j个系统部件，若是则值为1，否则为0。

步骤2 统计冲突集簇中系统部件的个数，根据系统部件的个数枚举出系统部件的所有可能的组合，即所有候选解。一般而言，将所有候选解按照部件编号从小到大，部件个数从少到多有序排列。将所有候选解按照指定规则转换为矩阵B。

集合与矩阵转换规则2规定如下：定义n×v参数矩阵，其中n为冲突集合簇中包含系统部件的个数，v为候选解的个数。矩阵中第x行第y列的值bxy表示第y个候选解中是否包含第x个系统部件，若是则值为1，否则为0。

步骤3 将矩阵A与矩阵B相乘得到m×v的参数矩阵C，即C=A×B。 矩阵C中第y列全为非0时，矩阵B中第y列对应的候选解为碰集。

步骤4 得到所有碰集后，删除其中的真超集，即可得到极小碰集。

2.2 算法验证

(1)充分性

aikbky=1时，当且仅当aik=1，bky=1， 即第i个冲突集中有第k个系统部件，第y个候选解中也有第k个系统部件。所以，第i个冲突集和第y个候选解有交集。

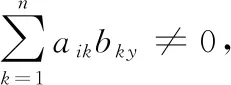
由碰集的定义可知，第y个候选解一定是一个碰集。充分性得证。

(2)必要性

设第y个候选解是一个碰集。

按照算法2.1，一定会有候选解符合要求，即碰集可以由算法2.1得到。必要性得证。

(3)正确性

算法的正确性体现在两个方面。

一方面，输入与输出之间的关系是正确的。输入数据是冲突集簇，冲突集簇转化为矩阵A，并根据其中部件个数生成矩阵B，其对应所有候选解。通过矩阵乘法运算，可以求出矩阵B中符合碰集条件的列，也就是从候选解中找出碰集，去超集之后就能输出所有极小碰集。

2.3 复杂度分析

假设该算法的总运行时间为T，主要与矩阵乘法运算的时间相关。在矩阵相乘得到矩阵C的过程中，求得矩阵C的每一个数值需要循环n次，时间复杂度为O(n)。每列包含m个数值，为了得到整列数值需要循环m次，时间复杂度为O(nm)。矩阵C有2n-1列，为了得到整个矩阵的数值需要循环2n-1次，时间复杂度为O(mn2n)。由于T≈O(mn2n)， 所以该算法的时间复杂度约为O(2n)。由于需要存储所有候选解，空间复杂度取决于候选解的个数。枚举得到候选解的个数为2n-1，算法的空间复杂度也为O(2n)。

3 实例执行

根据上述提出的基于矩阵求解极小碰集的算法和过程，举例分析如下：

例2：仍然考虑例1中的冲突集簇F={{1,2},{1,3},{1,2,3},{1,4},{2,4}}， 使用矩阵方法求解所有极小碰集具体步骤如下：

步骤1 冲突集簇包含5个冲突集，4个系统部件，构造5×4参数矩阵。第1个冲突集{1,2}包含第1个、第2个系统部件，所以矩阵中第1行的第1列和第2列(即a11和a12)为1；不包含第3个、第4个系统部件，所以第3列和第4列(即a13和a14)为0。同理，根据其它冲突集可以得到矩阵中其它数据，最终得到矩阵A如下

步骤2 冲突集簇中系统部件的数量为4，由4个部件可以枚举出15种组合，构造4×15参数矩阵。候选解有{1}、{2}、{1,2}、{3}、{1,3}、{2,3}、{1,2,3}、…、{1,2,3,4}。第1个候选解{1}包含第1个系统部件，不包含第2个、第3个、第4个系统部件，所以矩阵中第1列的第1行(即b11)为1，其它(即b21、b31和b41)全为0。同理，根据其它候选解可以得到矩阵中其它数据，最终得到矩阵B如下

步骤3 将上述两个矩阵相乘，得到一个5×15的新矩阵C

矩阵C中第3、7、9、11、13、14、15列的值全为非0，所以矩阵B中第3、7、9、11、13、14、15列对应的候选解为碰集

步骤4 矩阵B中第3列的第1行、第2行为1，第3行、第4行为0，所以第3个候选解包含第1个、第2个系统部件，不包含第3个、第4个系统部件，对应的集合为{1,2}。同理，矩阵B中第7、9、11、13、14、15列对应的集合为{1,2,3}、{1,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4}，即碰集有{1,2}、{1,2,3}、{1,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4}，去真超集得到极小碰集{1,2}、{1,4}、{2,3,4}。所以，{1,2}、{1,4}、{2,3,4}就是冲突集簇F的极小碰集，也就是系统的最小诊断解。

4 比较分析

为了分析算法求解效率，本节将基于矩阵求解极小碰集的算法与主流的树形结构算法进行比较，包括CSSE-Tree算法、HST-Tree算法。这里设置冲突集簇数据如下： {1,1+k}， {2,2+k}， {3,3+k}，…，{k,2k}。 其中，k表示冲突集簇中包含的集合个数。每一组数据测试10次，将平均值作为最后结果。运行环境为Windows10操作系统(Intel(R) Core(TM) i5-3427U CPU@1.80 GHz 2.30 GHz，4 GB内存)，使用Microsoft Visual C++6.0编程，运行结果见表1和图1。

表1 CSSE-Tree、HST-Tree和矩阵算法运行时间对比/ms

图1 CSSE-Tree、HST-Tree和矩阵算法运行时间对比

比较表1和图1中的数据，可以得出结论：①相对于这几种树形结构算法，本文提出的基于矩阵运算求解极小碰集的方法运行效率较好，具有一定优势；②当冲突集簇的集合个数k较小时，基于矩阵运算的方法没有优势，几种算法的运行时间相近。当集合个数k增加时，基于矩阵运算的方法时间长势最为平缓，运行时间不会随着冲突集簇中集合个数的增加而急速增长，因此，该算法更具有适用性；③基于矩阵运算的方法能求出所有极小碰集，不会丢失正确解。

通过分析算法运行结果，可以得出如下结论：①基于矩阵运算的极小碰集求解方法不需要生成结点和建立树形结构，数据结构简单，只需要数组就可以编程实现；②该算法计算过程较为简单，不需要递归调用，只需要进行简单的数学计算，运算速度较快；③该算法考虑所有可能解，并且不需要进行剪枝，因此不会丢失任何极小碰集；④当冲突集簇中的集合个数较多时，基于矩阵运算的方法具有比较明显的优势；⑤使用该算法求解极小碰集时，求解效率与冲突集的排列顺序无关，对于一个冲突集簇，无论冲突集排列顺序如何变化，算法运行时间不受影响。

综上所述，相较于CSSE-Tree、HST-Tree等算法，基于矩阵求解极小碰集的算法具有较好的效率，更适合应用于实际的故障诊断问题中。在给定特殊冲突集簇，比如冲突集簇的集合个数较多时，基于矩阵求解的运行效率明显高于其它算法。

5 结束语

自极小碰集问题提出至今，国内外大量专家学者投身于该问题的研究中，并且获得了丰硕的成果。本文提出一种全新的算法，基于矩阵运算求解极小碰集。该算法将集合簇以一种转换规则转换为矩阵，通过数学计算在矩阵中体现碰集的特性，从而求出所有极小碰集。与传统方法相比，该算法易于理解且编程简单，无需构造树，实现环境要求低，在大部分开发平台上都可实现，具有较高的求解效率，在某些情况下具有突出优势。通过矩阵运算排除碰集中的真超集，直接得到所有极小碰集，是未来进一步研究工作。