基于八叉树的卷积神经网络三维模型分割

杨晓文，李 静，韩 燮，韩慧妍，陶 谦

(中北大学 大数据学院，山西 太原 030051)

0 引 言

由于获取3D信息设备的不断发展，通过建模工具所创建的三维模型不断增多，对其进行研究成为热点问题。其中，三维模型的分割包括对点云与网格模型的分割，根据语义上的不同，把完整的三维模型分割为相邻子部分[1]。三维模型的分割有利于进一步理解和分析三维模型，包括变形、简化、检索以及曲面重建等[2]，同时也是古文物保护、建筑物及城市场景三维建模、动植物外形建模、医学检测、几何压缩与传输等工作的基础，在许多模型处理和视觉应用上也越来越重要。

1 相关研究

卷积神经网络(convolutional neural networks, CNN)不断应用在各领域中，国内外研究学者根据对三维形状的分析，利用卷积神经网络对三维模型的分割进行了研究，其中，主要为基于体素，流形以及多视图3类方法。

基于体素的方法是指以三维空间的体素作为定义域进行3D卷积，将CNN拓展到三维空间进行学习。Maturana等[3]将3D形状光栅化并在密集体素上采样距离函数，在整个体素上应用3D CNN。Wu NZ等[4]在体素上定义3D CNN以进行形状分析，提出了用于物体识别和形状分析的3D ShapeNets，但是该方法只适合于低分辨率的三维模型。为了降低基于全体素方法的计算成本，Graham B[5]提出了3D稀疏CNN，对于深层CNN，该方法的计算和存储成本仍然很高。这些方法计算量大，不易储存，不适用于高分辨率模型。

基于流形的方法是指对流形网格上定义的特征进行CNN操作。Boscaini等[6]将3D表面参数化为2D图像，将采样的特征图像馈送到CNN中以进行形状分析。Bronstein等[7]将CNN扩展到由不规则三角形网格定义的图形上。这些方法对于三维模型的等距变形较为稳健，但是它们被约束为平滑的流形网格时难以提取局部特征，噪声较大。

基于多视图的方法是指利用空间投影将三维模型转化为多个视图下的二维影像，并将图像堆栈作为2D CNN的输入。谢智歌等[8]提出了基于全卷积的多角度多层次极限学习机的三维模型分割方法，该方法通过对深度图像的多标签训练、预测以及把标签回投到三维模型的三角面片上得到分割结果。Kalogerakis等[9]设计了一个投影卷积网络应用于三维形状的分割。这些方法直接利用基于图像的CNN进行3D形状分析并处理高分辨率输入，但是不能确定视图数量以完全覆盖三维模型，无法避免遗失三维信息。

本文利用八叉树表示三维点云模型，将卷积计算限制在八叉树节点上，使计算量只和八叉树节点数目相关，卷积、反卷积、池化、反池化操作由于八叉树的数据和层次结构在迭代过程中计算高效，减少了计算与存储成本，避免了视图选择问题，可以处理高分辨率的点云输入。实验及评估度量结果表明，实验数据集中大多数模型取得了良好的分割效果。

2 背景知识

2.1 卷积神经网络

卷积神经网络是一种前馈神经网络，包含卷积计算并具有深层结构，其不断应用在深度学习中[10]。CNN的本质是多层感知机，局部连接和权值共享的方式减少了权值的数量更易于优化网络，降低模型的复杂度，减小过拟合的风险。通过构建多层网络提取数据中具有抽象语义信息的高层次特征，得到更好的特征鲁棒性。

CNN是基于监督学习的神经网络，实现特征提取功能的核心模块位于隐含层的卷积层和池化层，每层有多个特征图，每个特征图有多个神经元，并使用大小不等的卷积滤波器提取特征。其中，卷积层为特征提取层，通过权值共享的卷积核使每一层的特征都由上一层的局部区域激励得到，即将每个神经元的输入与上一层的局部感知野相连，并由激活函数形成并输出特征映射图[11]。池化层位于连续的卷积层中，用于压缩数据和参数量，去除冗余信息，防止过拟合。

2.2 八叉树结构

二维图像通常结构化表示为二维平面上的矩阵，但是三维形状是非结构化的，尤其点云数据是不规则和无序的。因此，利用卷积神经网络处理点云数据时，由于输入数据的不稳定性使得卷积操作难以直接应用到点云数据上。

利用自适应的空间剖分来压缩存储点云数据，八叉树[12]是一个非常好的选择。八叉树是一种递归、轴对齐且空间分隔的数据结构，将空间分成等体积的立方体可以加速细分运算，且单元大小的存储也可以节省空间。三维空间根据是否含有三维点云的一部分决定是否一分为八，并在子块里重复划分。八叉树结构常用于计算机几何进行优化碰撞检测、最邻近搜索等，且常用于三维数据的表达。

3 基于八叉树的卷积神经网络的三维模型分割

本文使用八叉树结构化表示三维点云模型，在点云模型的边界表面占据的稀疏八分体上执行CNN操作对三维点云模型进行分割。本文方法流程包括：①对点云模型进行预处理并在此基础上构建表示点云的八叉树结构，八叉树的最深叶节点处存储点云的信息，提取最大深度的叶子八分体中采样点云的平均法向量与平均曲率，并将其融合作为卷积网络的输入特征，存储在相对应的叶节点上；②将卷积计算限制在八叉树节点上，计算每个深度的相邻水平节点的特征，池化合并之后，将特征下采样到父节点并且被传送到下一八叉树深度层。级联反卷积神经网络进行逐点预测，遍历整个神经网络，不断迭代神经网络层训练并测试，得出点云模型分割预测标签；③使用CRF优化并进行分割可视化得出三维点云模型分割结果。本文方法流程如图1所示。

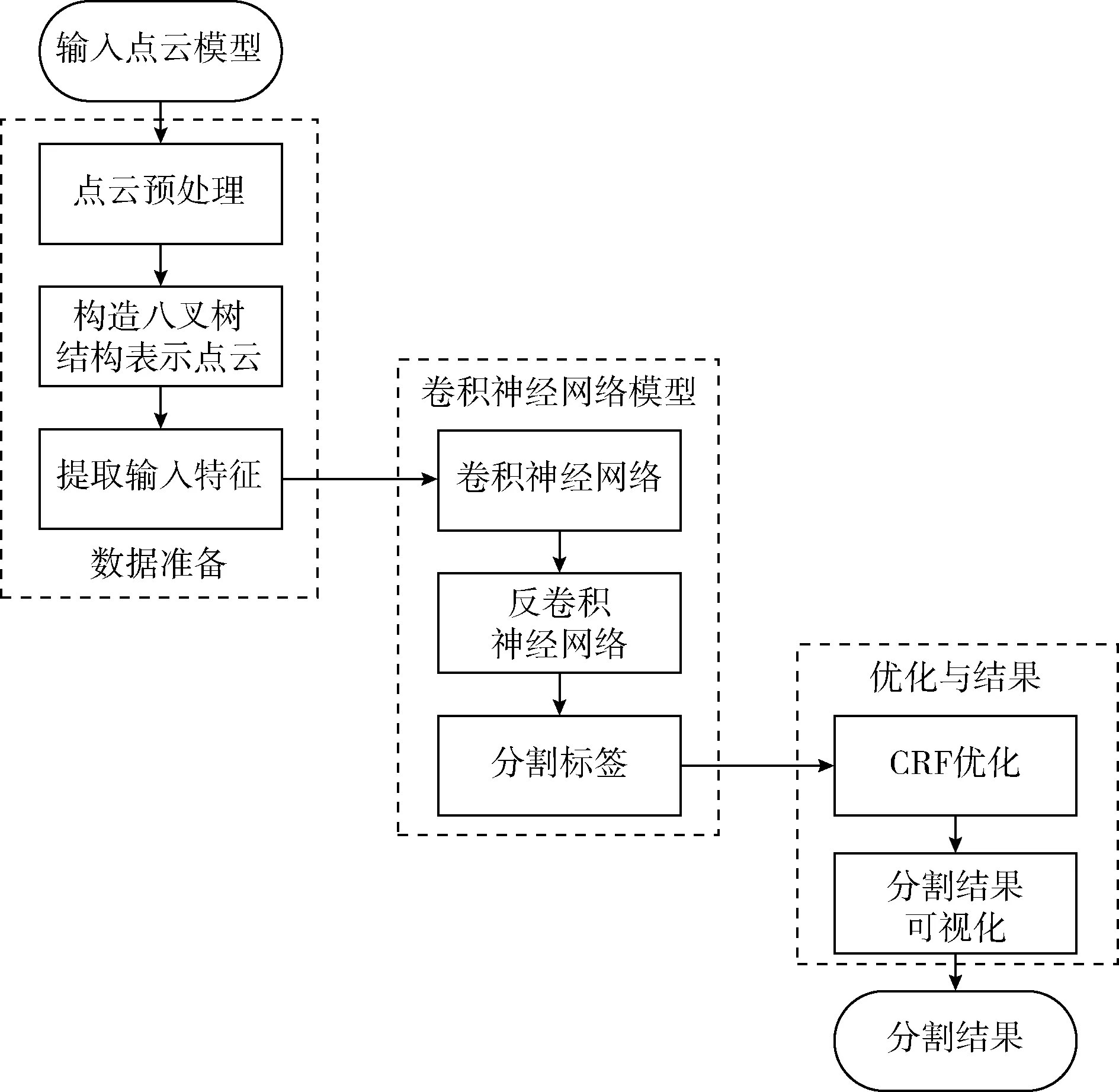
图1 本文方法流程

3.1 数据准备过程

3.1.1 点云预处理

实验所用原始模型是稀疏点云，并且点云模型缺失了对应的法线信息，为此将点云模型与相应的3D网格对齐，并将点投影到三角面片中，然后采用射线射击算法在三角网格中确定密集点，将密集点所在的三角面片的法线分配给该点，得到预处理的点云模型。射线射击算法具体来说，在将点云模型投影到三角面片的基础上，根据点云中每个点所在的三角面片确定包含该点云模型的边界立方体(该边界立方体是根据三角面片统一采样来确定的)，将多个虚拟相机均匀放置在包含点云模型的边界立方体的各个面中心，从每个方向均匀地对模型发射平行光线，计算光线与三角面片的交点，如果此三角面片中包含了点云模型中的点，即将该点的法线指向相机，不相交的点被舍弃，得到点云模型的密集点，以此预处理点云得到具有定向法线和密集点的点云数据。

3.1.2 构造八叉树结构

为了构造表示三维点云的八叉树结构，首先将三维点云模型缩放于轴对称的3D立方体中，然后采用广度优先算法，细分点云模型的边界立方体，并不断迭代，直到将深度为d处的点云模型边界所占据的所有非空八分体细分到下一深度d+1处的八个子八分体，即达到指定的八叉树深度，迭代停止。八叉树的每一层由排序后的随机键数组和标记非空节点序号的标签数组组成[13]，通过这些数组可以快速访问节点邻居。八叉树构造过程如图2所示。

图2 八叉树构造过程

其中，随机键是用来表示深度为d的八分体O在3D空间中的相对位置：key(O)∶x1y1z1x2y2z2..xdydzd,xiyizi∈{0，d}。 通过随机键升序排列八分体，第d深度的所有八分体中排序后的随机键存储在随机键矢量Sd中，矢量的长度是当前深度的八分体的数量，该矢量用于构建3D卷积中八分体的邻域。类比四叉树节点的随机键与每个深度的相应随机键数组如图3所示。

图3 四叉树随机键与标签

描述相邻深度的父子八分体之间的关系，通过池化操作将深度为d的八分体处计算得到的特征经过下采样计算后连接到深度为d+1的子八分体，并为非空八分体指定标签p， 并将该深度处的所有八分体的标签存储在标签矢量Ld中。详细定义请参见文献[13]。在第d深度的一个非空节点处定义索引j，计算第d+1深度处其第一个子八分体的索引k=8*(Ld[j]-1)， 从而可以快速找到父节点到其子节点的对应关系。类比四叉树每个深度的标签矢量如图3所示。

3.1.3 提取特征

构造点云的八叉树结构之后，提取最大深度的叶子八分体中采样点云的平均法向量[14]与平均曲率，两者相融合作为CNN的输入特征。对于空叶子八分体，将其指定为零向量作为输入特征；对于非空叶子八分体，对嵌入叶子八分体中的点云形状表面的一组点进行采样，利用点云预处理过程中分配给各点的定向法线计算平均法向量。

(1)

式中：NP(i) 表示点pi在该叶子八分体区域，N表示该叶子八分体内点的个数，pj是pi在此叶子八分体内的邻域点，从而得到pi的协方差如式(2)所示

(2)

式中：C是一个半正定矩阵，可以取3个非负特征值λi(i=0,1,2)。 当λ0<λ1<λ2， 并定义λi的对应正交特征向量为ni(i=0,1,2)， 又由式(3)所示

(3)

此时T(x) 表示点pi的最小二乘平面，近似看作点pi切平面。n0表示点pi在局部区域内的法矢，特征值λ表示为该曲面的变分。由Pualy等[16]定义可得该曲面变分近似于点pi处的曲率，如式(4)所示

(4)

并根据平均曲率定义求得点pi处平均曲率。

特征融合[16]是指从多个相关原始特征集中获得最具差异性的信息，能够消除因不同特征集之间的相关性而产生的冗余信息。本文方法中计算出平均法向量和平均曲率之后，利用并行特征融合策略将其合并成一个比单个输入特征更具有判别能力的特征并将其作为卷积神经网络的输入特征。并行特征融合策略的思想是：假设α，β是同一样本的两组特征向量，用复向量来表示样本的并行组合特征[16]，融合公式如式(5)所示

γ=α+iβ(i是虚数)

(5)

最后将融合后的特征作为卷积神经网络的输入特征并将其存储到输入特征矢量中。

3.2 卷积神经网络结构

卷积神经网络对点云的八叉树结构反复应用卷积和池化操作，本文中激活函数使用ReLU(f∶x∈R→max(0,x))， 并使用批量标准化(BN)来减少内部协变量偏移。将“convolution+BN+ReLU+pooling”作为基本单元，当卷积操作应用于深度为d的八分体时，由Ud表示，Ud的特征映射的通道数设置为2max(d，9-d)， 卷积核大小为3*3*3。 该部分网络结构定义为CNN(d)：输入→Ud→Ud-1→…→U2。

本文方法参考图像语义分割网络DeconvNet[17]，在卷积网络之后级联反卷积网络进行密集逐点预测。卷积网络被设置为CNN(d)，反卷积网络是CNN(d)的镜像，其中卷积和池化运算符由反卷积和上池化代替。将“unpooling+deconvolution+BN+ReLU”作为一个基本单位，将反卷积操作应用于深度为d的八分体时，则由DUd表示。所以整体卷积神经网络结构定义为： CNN(d)→DU2→DU3→…DUd。 网络结构如图4所示。

图4 网络结构

3.2.1 3D卷积

3D卷积(3D convolution)是指卷积核的维度为三维，最早提出用于行为识别等领域。在本文方法中，将卷积运算应用于某个深度处的所有八分体，需要在该八叉树深度处连接其相邻八分体，卷积运算φc如式(6)所示

(6)

3.2.2 池 化

池化(pooling)的目的是逐步压缩空间大小，是对卷积层输出的特征图做下采样操作。池化层在每个通道上独立运行，并在空间上调整其大小，去除冗余信息，最常见的形式是max-pooling和avy pooling，本文采用max-pooling操作。八叉树结构上应用max-pooling可以从每8个连续存储的子八分体属性值中挑选出最大值。

3.2.3 上池化

上池化(unpooling)操作是汇集和执行上采样的逆向操作，一般指的是max-pooling的逆过程，广泛用于CNN可视化和图像分割。应用max-pooling之后，每个池区域中最大值的位置记录并存储在一组变量中，这些变量将当前特征映射放入上采样特征映射的适当位置。在CNN中，最大池化操作是不可逆的，可以通过使用一组转换变量记录每个池化区域内最大值的位置获得一个近似的逆操作结果。

3.2.4 反卷积

反卷积(deconvolution)，也称为转置卷积和反向卷积，用来放大和加密特征图，步长为k的反卷积核可以实现特征图的k倍放大效果。卷积层的反向传播过程是反卷积层的前向传播过程，基于先前描述的八叉树上的卷积操作，可以相应地实现反卷积操作。

3.2.5 神经网络优化算法

(7)

ωt+1=ωt+Vt+1

(8)

其中， ∂是负梯度的学习率(base_lr),μ是上一次梯度值的权重(momentum)，用来加权之前梯度对现在梯度下降方向的影响，这两个参数值需要通过不断调整得到最合适的值。

3.2.6 损失函数

损失函数[19]在CNN中是用来衡量预测标签与初始标签一致性的度量指标。本文中使用SoftmaxWithLoss计算训练过程中的损失值，卷积过程中，SoftmaxWithLossLayer主要使用了两个概率统计原理：逻辑回归和最大似然估计。

逻辑回归对应于Softmax,其将神经网络的输出特征转化成概率，最大似然估计用于计算损失函数，其核心公式如式(9)、式(10)所示

(9)

(10)

其中，yi为标签值，k为输入点云标签所对应的神经元，m为输出的最大值，主要考虑数值稳定性。而反向传播时loss计算公式如式(11)所示

(11)

对输入的zk求导可得式(12)

(12)

3.3 CRF优化

本文使用条件随机场CRF(conditional random field algorithm)[20]优化分割结果。由于反卷积网络分别对每个点进行预测，分割后的点云模型中相邻区域之间仍然存在噪声，因此使用CRF对结果进行调整。

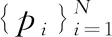
E(x)=∑iφu(xi)+∑i

(13)

式中：i和j的范围从1到N。φu(xi) 用来约束最终输出结果，定义为φu(xi)=-log(p(xi))， 其中p(xi) 是神经网络生成标签的概率。φp(xi,xj) 用于合并信息以输出精确结果，如式(14)所示

(14)

式中：Wθi表示具有标准差θi的高斯函数，μ(xi,xj) 是标签函数，ωi和θi是超参数。通过CRF优化算法之后，点云模型的不同分割区域之间噪声减小，边缘更平滑。

4 实验讨论

4.1 数据集与实验环境

本文实验使用数据集ShapeNetCore的一个子集，包含16种形状类别，大约17 000个点云模型，每个类别有2到6个部分，总共有50类不同区域的标签注释。在实验中，对于每一类的点云模型分别以模型总数90%的数据量作训练数据，10%的数据量作测试数据。

实验环境：以Caffe为深度学习框架，支持GPU运算；Intel(R)Core(TM)i7，CPU@2.80 GHz，NVIDIA GeForce GTX 1050 Ti 4 GB，VS2015+anaconda 3.4.2，CUDA8.0+cudnn-8.0-windows10-x64-v5.0。

4.2 训练与测试

实验中神经网络的参数和函数设置见表1。网络模型采用SDG优化算法，迭代学习中随机均匀采样训练数据，更新模型参数，逐层调节权重参数，使用SoftmaxWithLoss通过大量的迭代训练提高网络的精度，并计算迭代过程中的损失值。针对不同类别的个别参数进行调整，其中基础学习率变化范围在0.1到0.001之间；批量大小和测试间隔随测试集的数量大小进行调整，调整规则为2的整数次幂；最大迭代数根据训练集的大小调整。

表1 实验参数/函数设置

在卷积神经网络训练过程中，训练与测试同时进行，并将测试间隔设置为200，即每训练200次测试一次，同时计算各自的准确率与损失值。在训练迭代结束后，生成caffemodel(caffemodel里不仅存储了权重和偏置等信息，还存储了整个训练网络的结构信息)。在测试阶段，调用每个类别的caffemodel获得每个最精细叶节点的输出标签和预测概率，此时可以得到通过神经网络输出的逐点的预测标签。

4.3 结果与对比

本文使用pcl工具可视化分割结果。简单来说，使用八叉树结构中的叶节点表示点云模型，使用神经网络得到的预测标签分别以不同颜色分类显示分割结果的不同区域。经过CRF优化之后，本文方法得到的分割效果如图5所示。

图5 本文方法应用于ShapeNetCore子集的分割效果

本文还分别使用PointNet[21]，SpecCNN[22]，O-CNN(5)[13]，O-CNN(6)[13]，SPGN[23]的方法进行实验并且与本文方法进行比较，如图6所示，可以看出，O-CNN(6)方法在模型右侧椅腿与椅座连接处噪声明显，本文方法则在分割相邻区域处以及边界处噪声较小，边缘更平滑，分割效果更好。为了更准确地描述分割效果的优劣，采用IoU(intersection over union)标准对以上不同方法和本文方法进行度量，该标准用于测量实际标签值和预测标签值之间的相关度，相关度越高，度量值越高，分割效果越好，对比结果见表2。对比结果表明，本文方法对飞机，椅子，汽车，吉他等三维点云模型都有较好的分割结果。

图6 O-CNN(6)分割结果(a)与本文结果(b)对比

5 结束语

本文针对三维点云数据的计算量大以及存储成本高的问题，使用八叉树数据结构表示三维点云模型，同时为了避免显式的特征提取带来的局限性，使用两种基础特征相融合作为卷积神经网络的输入特征，利用卷积神经网络级联反卷积神经网络对三维点云模型进行分割，实现了分割结果可视化，提高了实验数据集中大多数类别的分割准确率。但是由于使用八叉树结构表示点云模型，对于部分类的分割结果的分割区域之间存在噪声，模型边界处锯齿状明显，在分割可视化时部分模型效果欠佳。其次由于数据量不同以及在训练过程中存在拟合问题使各类点云的预测标签存在误差，需要进一步研究处理。

表2 以IoU为评价度量的对比结果