三维十字链表八叉树的高效检索实现
谭玉玲
(1.罗定职业技术学院 信息工程系,广东 罗定 527200;2.北京师范大学 教育技术学院,北京 100082)
0 引言
三维激光扫描技术是测绘领域出现的一个新的技术。点云(point cloud)是在同一个空间的参考系下描述现在目标空间的分布和现在目标的表面特征的大量点的集合[1]。三维激光扫描技术能够给出扫描物体表面所有三维点云的信息,所以可以用其获得精确、高分辨率的数字地形模型[2]。
空间数据结构在早期主要用于空间数据库及地理信息系统,将其用于三维点云数据结构的研究时,可以明显地提高点云数据的查询效率[3]。在空间数据结构技术研究中,出现了大量不同的算法,其中包括KD树、八叉树等[4-5]。如何提高三维点云信息数据的查询、检索效率是三维点云信息系统数据架构的关键问题。
现有的 KD 树、八叉树可以在二维空间中取得理想效果[6],但是将其拓宽到更高层次的维度空间后,就很难完全满足高维度空间组织和管理的需求[7]。另外,在基于空间的数据结构计算算法中,KD 树、八叉树等基于空间结构计算的方式通常都是针对某一类物体,不具备该算法的应用广泛性,应用范围也就有所限制[8]。因此,面对这种情况,运用其中一种数据架构难以满足点云数据快速发展的需要。
本文提出了构建三维十字链表八叉树的高维度数据结构的方案。在八叉树的基础上,利用十字链表,将三个维度方向的叶子节点链接起来,这样可以有效地缩短查找点的时间以及减少时间复杂度;通过对三维八叉树和三维十字链表八叉树比较分析后发现,该算法提高了三维点云的数据查询和检索效率。
1 算法设计
用于表示物体表面信息的点云具有“稀疏性”[9],即点云空间中绝大部分没有点。在使用基于坐标的八叉树数据结构描述的点云空间中,存在“空体素”,而深度学习遍历算法的计算时要求逐个遍历相邻空间组。而八叉树本身的树形结构决定了其无法直接访问兄弟节点,即无法以O(1)的时间复杂度直接访问同级“体素”。进一步来说,基于坐标的八叉树数据结构也无法在访问“体素”前确认当前体素内是否有点,即无法做到直接跳过“空体素”。如果不对此做优化而直接使用基于坐标的八叉树数据结构描述点云空间,那么在遍历点云空间时,点云的“稀疏性”就会导致大量的时间浪费在询问“点云是否为空”等操作上,而真正有效的计算操作比例却非常低。因此,需要借用十字链表的思想,将沿着每个维度坐标方向的“非空”体素首尾相接,方便点云算法直接略过所有“空体素”,以期提升访问点云的效率。
2 三维十字链表八叉树的定义及基本操作
2.1 定义
三维十字链表八叉树是一种用于描述三维空间的树状数据结构,其中的每个节点表示1个正方体的体积元素,每个节点有8个子节点,将8个子节点所表示的体积元素加在一起就等于父节点的体积[11]。“十字”是指任意两个维度间互不相干,使用线性代数表达为线性无关。 “链表”是指每个维度方向上两个相邻元素的关联方式为链表。使用链表的好处是可以跳过相邻元素间的空白空间,以O(1)的时间复杂度访问当前元素的相邻元素。
2.2 基本操作
三维十字链表八叉树的基本操作分为以下五个步骤。
2.2.1 判断沿某个坐标轴方向是否为头(尾)节点
(1)确定一个坐标轴方向;
(2)沿这个坐标轴方向判断该坐标点的前驱是否为空,后继是否为空;
(3)若前驱为空,后继不为空,则该坐标点是头节点;
(4)若前驱不为空,后继为空,则该坐标点是尾节点。
2.2.2 判断某个元素沿某个坐标轴是否有前驱(后继)节点
(1)确定一个坐标轴方向;
(2)沿这个坐标轴方向判断该坐标点的前驱是否为空,后继是否为空;
(3)若前驱不为空,则该坐标点有前驱节点;
(4)若后继不为空,则该坐标点有后继节点。
2.2.3 添加一个元素
(1)判断这个元素是否存在,若存在则进入下一步;
(2)若添加的元素为某一维度上的第一个节点,则将该节点的前驱设为空,该节点的后继为之前的第一个节点,并且将之前的第一个节点的前驱设为现在新添加的节点;
(3)若添加的元素是中间节点,则该节点的前驱是添加位置的前一个结点,该节点的后继是添加位置的后一个节点,前一个结点的后继是该节点,后一个结点的前驱是该结点;
(4)若添加的元素是最后一个节点,则该节点的前驱为之前的最后一个节点,该节点的后继为空。
如图1所示,在图中添加一个点C,变成图2。首先判断点C不存在于图1中,然而确是图2中点B第二维度方向上的第一个节点,所以将点C的前驱设为空,该节点的后继为点B节点,而且将点B的前驱设为新添加的点C节点。
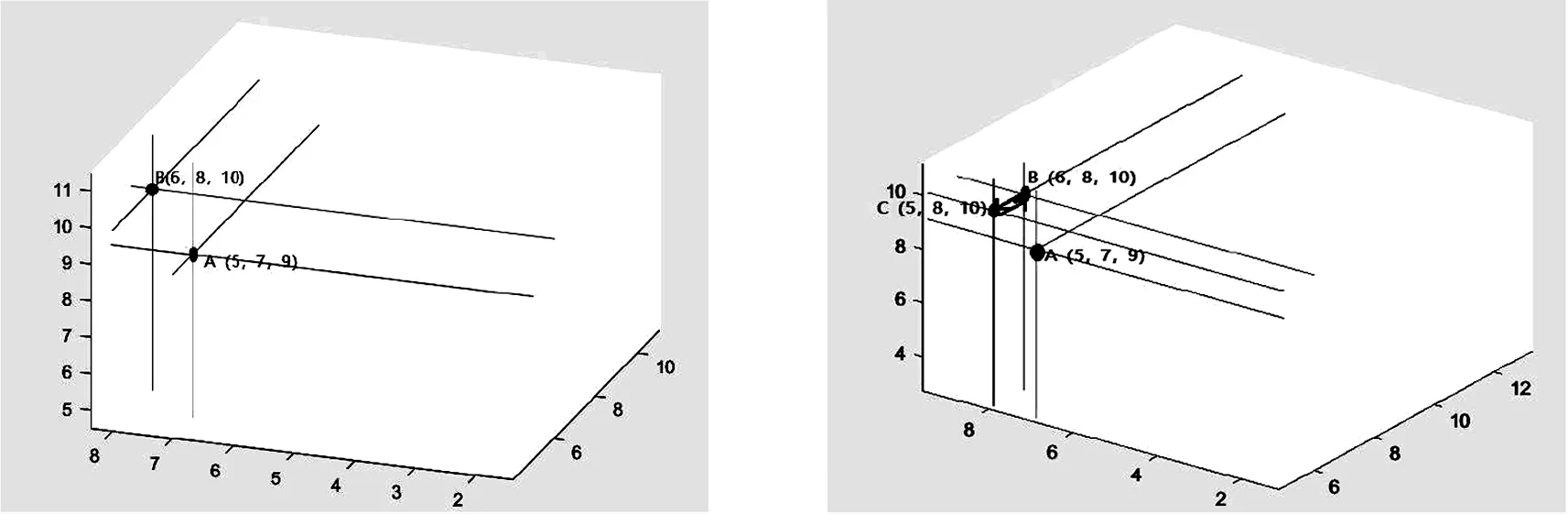
图1 当前三维十字链表八叉树 图2 三维十字链表八叉树添加点
2.2.4 删除一个元素
(1)判断这个元素是否存在,若存在则进入下一步;
(2)将每个维度上的该元素的前驱、后继关系均设为nullptr;
(3)若删除的元素是某一维度的第一个节点,则将头节点修改为该维度上的下一个节点;
(4)若删除的元素是某一维度的中间节点,则该节点的前驱节点是该节点的后继节点的前驱,该节点的后继节点是该节点前驱节点的后继;
(5)若删除的元素是某一维度的最后一个节点,则该节点的前驱节点的后继设为空。
在图2中删除存在的点C,结果如图3所示。首先判断点C存在于图2中,然后将每个维度上的点C的前驱、后继关系均设为nullptr。删除的点C是点B的第二维度上的第一个节点,头节点需要修改为该维度上的点B节点。
在图4中删除不存在的点D,结果如下图所示。在图2中首先判断不存在点D,然后抛出异常。
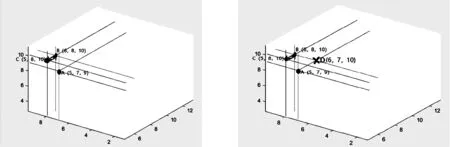
图3 三维十字链表八叉树成功删除点 图4三维十字链表八叉树失败删除点
2.2.5 迭代遍历
使用32个点在深度为4的三维十字链表八叉树中进行迭代遍历访问。访问过程中,以第三维度(z)为准进行迭代顺序访问。如图5所示,三维十字链表八叉树中存在3个点,分别是点A、点B、点C。在迭代遍历访问中,依据上述迭代遍历描述具体过程,首先访问点A(5,7,9),然后访问点C(5,8,10),最后再访问点B(6,8,10)。
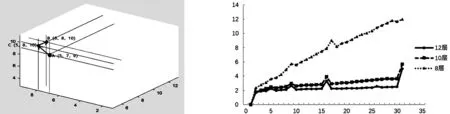
图5 迭代遍历 图6 插入点的效率对比
3 试验分析
3.1 试验平台
该试验是通过读取PLY文件获得点云的数据[12],主要是在Windows10 64位操作系统上进行的。设备的配置信息:处理器是Intel Core i5-8250U,GPU是UHD,内存8 G,实验中使用Ubuntu 20.04 LTS、Clion。试验中使用了300万个点。
3.2 试验结果分析
3.2.1 分析测试插入点的效率
从图6可以看出:(1)随着点数的增大,耗时的基本规律是:8层>10层>12层;点数越大,不同层的耗时越多;8层的均值波动最小;层数越多,均值耗时越少。(2)均值图上有几个点比较突出,剩余的基本都是线性增长。其原因在于:C++自带的标准库的容器不是用一个开一个空间,而是先开一部分空间,然后连续往里存,用完了以后再开空间,所以开空间比较耗时。(3)层数越多,均值耗时越少。原因在于:层数越多意味着空间就越大,点不变的情况下,平均密度就越低,点所在体素重复概率就越低。
3.2.2 对比实验
下面对本文提出的三维十字链表八叉树和三维八叉树[13-15]的效率进行对比。其中,黑色实线条表示三维十字链表八叉树,而黑色虚线条表示三维八叉树。
(1)插入数据的效率对比
试验结果如图7至图9所示。在深度为8插入点时,随着点数的增加,总体来说,三维十字链表八叉树比三维八叉树耗时短,不过,其中有一段它们的耗时一样;在深度为10和12插入点时,随着点数的增加,总体来说,三维十字链表八叉树比三维八叉树耗时短。试验结果表明,随着点数的增加,在不同深度的情况下,三维十字链表八叉树的插入数据的效率比三维八叉树更好。

图7 插入点的对比(8层) 图8 插入点的对比(10层)
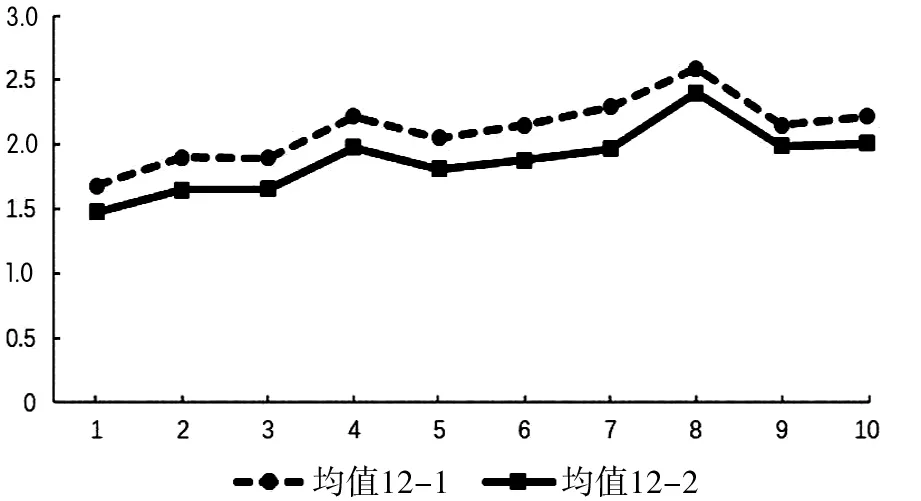
图9 插入点的对比(12层)
(2)查找数据的效率对比
试验结果如图10至图12所示。在深度为8查找点时,随着点数的增加,总体来说,三维十字链表八叉树比三维八叉树的耗时短;但是其中有两个特别的点值得关注,它们分别是:当点数增加到30万查找点时,三维八叉树的耗时比三维十字链表八叉树的短;当点数增加到大约100万查找点时,三维十字链表八叉树和三维八叉树的耗时一样。
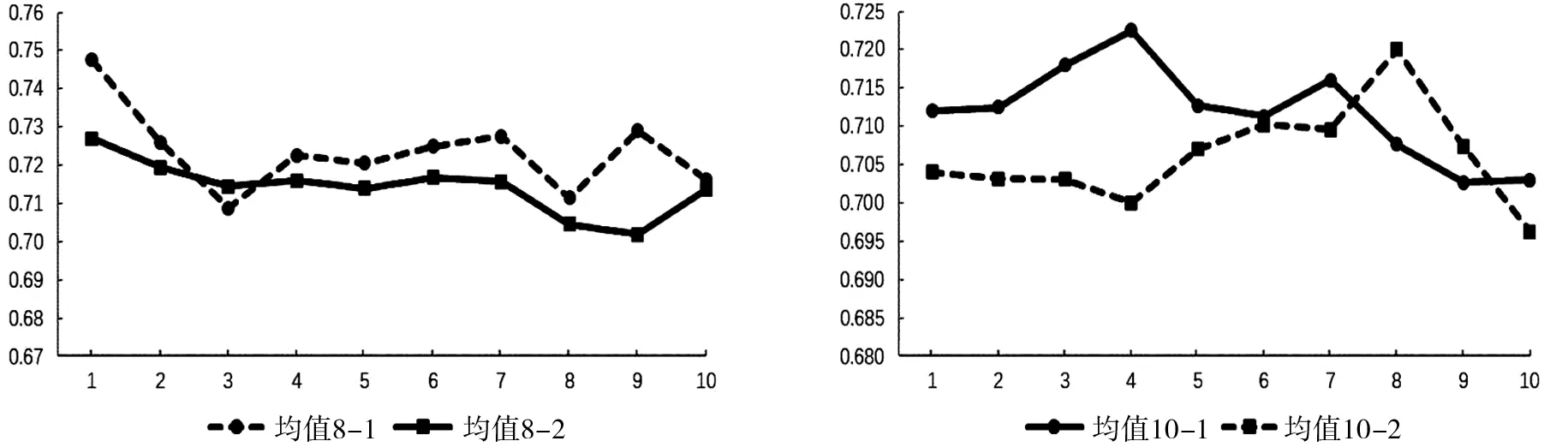
图10 查找点的对比(8层) 图11 查找点的对比(10层)
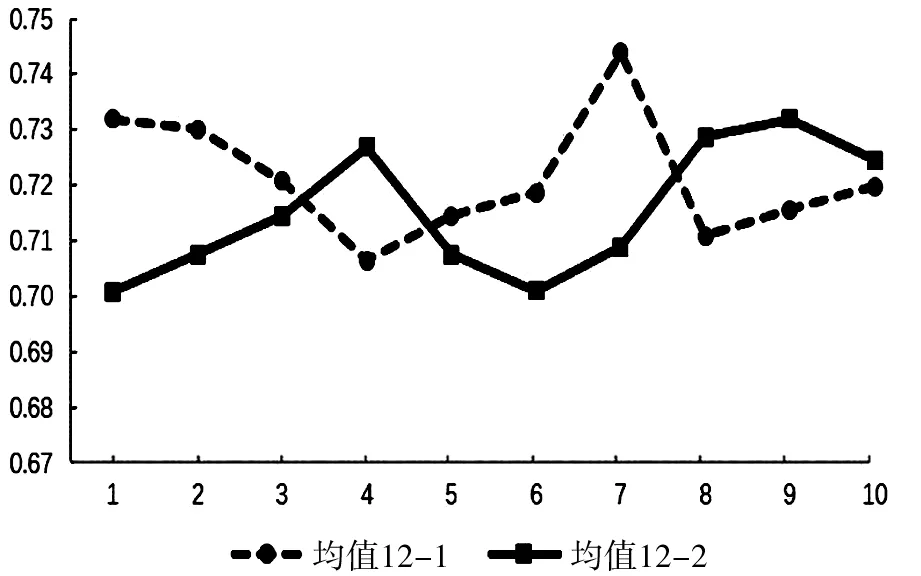
图12 查找点的对比(12层)
在深度为10查找点时,随着点数的增加,总体来说,三维十字链表八叉树比三维八叉树的耗时短;但是有一个特殊的时间段,当点数增加到75万至95万这个区域时,三维八叉树的耗时比三维十字链表八叉树的短。
在深度为12查找点时,随着点数的增加,有两个特殊的时间段,分别是:当点数增加到32万至47万这个区域时,三维八叉树的耗时比三维十字链表八叉树更短;当点数增加到75万至100万这个区域时,三维八叉树的耗时比三维十字链表八叉树更短。其他的地方都是三维十字链表八叉树比三维八叉树耗时短。
试验结果表明,随着点数的增加,在不同深度的情况下,总体来说,三维十字链表八叉树查找数据的效率比三维八叉树好,但是也会有特殊的时间段出现了三维八叉树的耗时更短的情况。
(3)删除数据的效率对比
试验结果如图13至图15所示。在深度为8删除点时,随着点数的增加,总体来说,三维十字链表八叉树和三维八叉树的耗时几乎一样。
在深度为10删除点时,随着点数的增加,只有在点数为20万至40万这个区域时,三维十字链表八叉树比三维八叉树耗时短,其他的地方均是三维八叉树的耗时更短。
在深度为12删除点时,随着点数的增加,当点数到达50万之后,三维十字链表八叉树比三维八叉树的耗时更短。
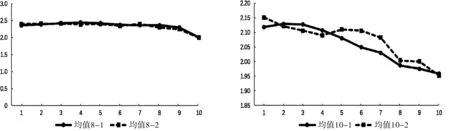
图13 删除点的对比(8层) 图14 删除点的对比(10层)

图15 删除点的对比(12层)
总体而言,试验数据证实,随着点数的增加,在不同深度的情况下,当深度越深,点数达到一定条件时,三维十字链表八叉树的删除数据的效率比三维八叉树更好。这也说明三维十字链表八叉树更适合稀疏空间的情况。
4 结论
本文通过对三维点云空间中领点数据结构的高效检索情况的研究,发现传统的三维八叉树的数据结构对数据信息保存存在一定的问题,并且三维八叉树的数据结构对点云的领点查找速度也有待提高。基于这些问题,本文提出通过设计三维十字链表八叉树的数据结构去实现三维点云空间中领点数据结构的高效检索。本文设计了三维八叉树和三维十字链表八叉树在插入、删除、查找三个方面的检索效率的试验。通过试验得出,三维十字链表八叉树在稀疏空间中的优势更加明显。

