基于改进的Otsu方法的钢渣彩色图像分割
严晨曦,熊 凌+
(1.武汉科技大学 机器人与智能系统研究院,湖北 武汉 430081;2.武汉科技大学 信息科学与工程学院,湖北 武汉 430081)
0 引 言
炼钢造渣是炼钢工艺中必不可少的一环[1]。转炉下渣时,钢渣漂浮在钢水表面并且伴随着钢水一同进入出钢口,这就需要我们及时检测钢水中的夹渣情况并控制钢渣含量,减少钢渣对钢水纯净度的影响。另外,在连铸生产过程中,钢水中钢渣含量过多会造成出钢口的堵塞,钢渣中的二氧化硅、氧化铁和氧化锰等化学物质增加了钢水的氧化程度,导致冷轧钢板的表面质量下降,减少其使用寿命,造成严重的经济效益损失[2]。因此对钢水中的钢渣进行分割来减少钢水的夹渣量,提高钢水的纯净度具有重要的意义。传统的人眼观测法其观察结果具有较大的主观性,因此钢渣分割效果不佳。为了使钢渣能够较为完整的从钢水中分离出来,国内外学者提出了许多钢渣特征提取的图像处理方法,通过提取钢渣的颜色、几何形状、尺寸等特征来达到更好的分割效果,以实现钢水含渣情况的检测[3]。
钢渣图像分割是实现钢渣实时检测的关键步骤之一。分割技术以往通常采用的是钢渣灰度图像,但灰度图像会缺失很多重要的特征信息从而导致图像分割效果不理想。而彩色图像比灰度图像能够提供颜色、亮度、饱和度等更多的特征信息,因此灰度图像分割方法不适用于彩色图像分割[4]。研究彩色图像分割具有重大意义,对彩色钢渣图像进行分割,就要选择恰当的色彩空间,从而提取出钢渣图像的颜色特征,能更容易将目标提取出来,从而提高钢渣检测的精确度和钢水的纯净度。就彩色图像分割而言,需要分析图像的各种特征信息来选择合适的色彩空间,然而目前所有的颜色空间中任何一种都不能代表全部色彩及色彩组合。
为了解决彩色钢渣图像目标与背景区域颜色存在较大差异的问题,现已提出了基于彩色空间聚类[5]的分割方法。然而,要想得到理想的分割效果,单独使用基于彩色空间聚类的分割方法是无法实现的。所以需要对分割后的钢渣图像进行二次分割,常用的方法为Otsu方法[6],但Otsu方法只针对灰度直方图为单峰或双峰图像,而钢渣图像一般为多峰图像,因此需要对其进行改进以达到分割效果。为了准确的将钢渣从钢水中分割出来,本文利用基于Lab颜色空间的K均值聚类算法对彩色图像进行预处理并提出了一种改进的Otsu方法的图像分割算法。在Lab颜色空间[7]利用K-means聚类算法[8]对彩色钢渣图像进行预处理,对预处理后的图像用改进的Otsu方法进行阈值分割,实现了钢渣图像的有效分割。
1 K-means算法
1.1 Lab颜色空间转换
为了实现钢渣图像的有效分割,就要选择恰当的颜色空间。本文将图像的RGB非均匀颜色空间[9]转换到Lab均匀彩色空间,实现空间分割的选择。Lab颜色空间中的3个相互垂直分量L、a、b用坐标轴x、y和z表示,所有颜色特征通过它们的组合得到。
首先将RGB空间转换到CIEXYZ空间,如式(1)所示

(1)
其中

(2)
然后将XYZ空间转换到典型的均匀Lab颜色空间,如下式所示
(3)
(4)
其中,RGB三颜色通道取值范围均为[0,255],由上述公式可计算出X、Y、Z的值,一般默认Xn、Yn、Zn的值分别为95.047、100.0、108.883。
1.2 K均值聚类方法
将RGB图像转换到Lab颜色空间之后,然后用K均值聚类算法实现图像样本点特征空间的分割。K均值聚类算法如下:
设样本集合X={xi|xi∈Rd,i=1,2,…,n} 由n个像素点组成,每个像素点xi由表示其特征的b个数据构成。K均值聚类的目的是将n个像素点划分为k类并形成k个聚类中心,其构成的数据集为C={ck|k=1,2,…,k}, 其中σk为ck的聚类中心。定义欧氏距离
(5)
式中:n个像素点分别被划分到ck类,则所有被划分到ck类的像素点到其所属类别的聚类中心的欧氏距离之和为
(6)
将聚类中的每个子类统计一次则得到所有像素点到其所属类别的聚类中心的欧氏距离之和为
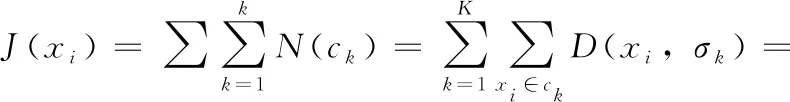
(7)

1.3 K均值聚类彩色图像分割
针对彩色图像像素数据的3个相互垂直颜色分量之间存在高度线性相关的问题,本文采用基于Lab颜色空间的K均值聚类算法对彩色钢渣图像进行预处理,将图像聚为4类,其分割结果如图1(b)所示,图1(c)和图1(d)分别为RGB空间和HSI空间的分割结果。图2为提取目标所在类簇的分割图像。

图1 不同空间下K均值分割图像

图2 Lab空间K均值分割图像
从图1(b)可以看出,基于LAB空间的K均值聚类方法能够较为准确将钢渣聚为一类,而在RGB空间和HIS空间中,部分背景会被划分到钢渣那一类中,出现了过分割的情况,不能准确将钢渣单独聚为一类。
在进行K均值聚类时,Lab颜色空间能够较好地消除3个相互垂直颜色分量之间存在的高度线性相关,从图2(b)中可以看出,钢水亮光与钢渣颜色近似,所以K均值算法将其与钢渣划分为同一类,将钢渣与钢水亮光从背景中分割了出来,实现了第一次分割,但本文目标是将钢渣完整分割出来而将钢水亮光分割为背景,所以需要对其进行第二次分割。
2 钢渣灰度图像阈值分割
2.1 传统Otsu阈值分割方法
Otsu算法即最大类间方差法,该算法定义请参见文献[10]。算法的基本原理为:设一幅图像为I,图像灰度值的取值范围为 [0,L-1], 用N表示像素总数,ni表示灰度级为i(i∈[0,L-1]) 的像素点数,pi表示所有灰度级为i的像素点出现的概率,则有
pi=ni/N
(8)
目标区域比例为
(9)
背景区域比例为
(10)
目标均值为
(11)
背景均值为
(12)
总均值为
(13)
类间方差计算公式为
(14)
Otsu法最大类间判断准则下的最佳阈值选取公式为
(15)
2.2 改进Otsu阈值分割方法
针对传统的Otsu方法对于灰度直方图为多峰的图像无法获得较好分割效果的问题,WOV法即目标方差加权法[11]能够很好地解决这个问题,其计算公式如式(16)所示
(16)

图3 钢渣灰度图像及其直方图

图4 Otsu方法和WOV方法分割效果
综上所述,对于灰度直方图呈现多峰的钢渣图像且钢渣本身灰度值比灰度均值大的情况,目标方差加权法并不适用,无法得到理想的分割效果。

(17)
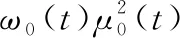
(18)
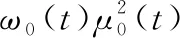
2.3 总算法实现
本文用基于Lab空间的K均值聚类算法和改进的最大类间方差法对彩色钢渣图像进行分割。将待分割的彩色钢渣图像从RGB颜色空间转换到Lab均匀颜色空间后,然后依次对图像进行处理,最后分割出目标,实现分割效果,算法流程如图5所示。

图5 总算法流程
2.4 图像分割结果的评价
为评价图像分割效果的优劣,选取均方误差(mean square error,MSE)作为衡量图像分割性能好坏的指标对不同分割算法的性能进行评价。MSE表示经阈值分割后图像被错误分割的概率,均方误差定义为
(19)
式中:X(i,j) 表示大小为M×N的标准图像,Y(i,j) 表示分割后的图像。由于没有标准分割图像,实验时采用直方图观察法确定最佳阈值,最佳阈值分割后的图像即为标准分割图像。MSE越小,表示目标被错分为背景的像素点越少,分割的效果越好,其取值范围为[0,1]。0表示没有被错分的情况,1表示完全被错分的情况。
3 实验结果分析
在Matlab2016a平台上进行仿真实验,选取了两张钢渣图像和一张红外下渣图像,3张钢渣图像都是目标灰度值大于平均灰度值的彩色图像,用Lab空间的K均值算法预处理后,然后用最大类间方差法和改进最大类间方差法进行第二次分割,分割对比实验如图6所示。
本文选取了2张钢渣图片和一张红外下渣图片,用K均值聚类算法对彩色钢渣图像进行第一次分割后,降低了背景的复杂程度。从阈值分割后的图像可以看出,最大类间方差法未能将钢渣完整分割出来,部分钢渣亮光被误分割为目标,而改进的最大类间方差法减小了钢渣亮光对目标区域钢渣的影响,能够较为准确的将钢渣分割出来。

图6 钢渣图像分割对比
表1和表2分别为两种分割方法的最佳阈值对比和性能对比。

表1 两种分割方法阈值对比

表2 两种分割方法性能对比
由表1可以看出,改进后的阈值大于最大类间方差法,有效地避免了阈值偏低将钢渣亮光误分为目标。由表2可以看出,改进最大类间方差法耗时较短,分割误差也有所减小。
为了进一步分析实验结果,不用K均值聚类对上述3张原始图像进行预处理,而直接用传统Otsu法、迭代法和最大熵法对3张原始图像进行分割,然后与本文提出的方法进行对比,实验结果如图7所示。
从图7可以看出,直接用其它3种算法对彩色钢渣图像进行分割时,局部细节信息模糊,没有将钢渣完整的从钢水中分割出来。其中,最大熵法分割效果最差,大量背景像素点被误划分到目标那一类,而本文方法能够较为准确地将钢渣从复杂的背景中分割出来,获得了较理想的分割效果。
表3和表4分别为4种分割方法的阈值对比和性能对比。
由表3可以看出本文方法的最佳分割阈值大于其它 4种分割阈值,与理想阈值更为接近。从表4可以看出本文方法耗时与其它4种方法相差不大。用最大类间方差法和迭代法对原图1、原图2和原图3进行分割时,MSE值相差不大,所以分割效果也近乎相同。最大熵法的MSE值最大,所以分割效果最差。而本文方法MSE值最小且接近0,表明了本文方法分割效果较其它3种方法分割效果更好一些。
4 结束语
在对彩色钢渣图像进行分割时,无法通过单一方法将钢渣从钢水中完全分离,当图像中钢渣亮光与目标部分方差差别较小时,运用Otsu法得到的阈值将会偏小,从而使分割阈值过低而导致错分。本文提出的基于Lab颜色空间的K均值聚类和改进Otsu法分割的融合算法,先利用K均值算法将彩色图像中钢渣亮光与钢渣从背景中分离;再通过对传统Otsu算法中最优阈值选取公式进行分析,在WOV方法的基础上,利用背景大小在图像中的比例,修改最优阈值判别选取公式,解决了阈值偏低误将部分钢渣亮光划分到目标的问题,并提高了算法执行速度,降低了分类误差以及改善了分割效果。

图7 不同方法分割对比

表3 4种分割方法阈值对比

表4 4种分割方法性能对比

