等截面消声管道传递损失计算的简化方法∗
杨 亮 孙红灵 杨 军
(1 中国科学院噪声与振动重点实验室(声学研究所) 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
管道消声系统在噪声控制工程中广泛使用,其声学性能的准确快速仿真预测具有重要意义。管道声学问题的求解主要包括解析方法和数值方法。解析方法[1]一般计算速度快且计算精度高,包括以传递矩阵法为代表的一维解析方法以及以模态匹配法为代表的三维解析方法,通常情况下,解析方法只适用于简单规则结构的声学计算,很多情况下并不满足实际工程的计算需求。三维数值方法(主要包括有限元方法[2−3]和边界元方法[4])理论上可以计算任意复杂形式管道的声学性能,但消声管道一般长度较长、截面尺寸较大,且通常考虑计算的频率范围较宽,如果进行三维数值仿真将花费较多的计算时间,并不适用于消声管道的前期设计优化。近年来,以快速多极边界元[5]为代表的快速算法得到了较快的发展并在声学计算领域日趋成熟,一些商业软件也集成了这一算法,但是目前商业软件中的快速多极边界元还不能考虑管道中包含吸声材料的情况,无法应用于消声管道的声学计算。另外,以有限体积法为代表的时域方法[6]由于可以考虑复杂流动对声场的影响而得到了广泛的关注,但是时域法的计算对计算环境的要求过高,目前还很难应用于实际管道声学问题的求解。
综上所述,针对消声管道的声学性能计算,现有的方法存在一些不足,适用于大尺寸消声管道优化设计的声学计算方法需要进一步研究。消声管道的声学性能计算虽然本质上是三维声学问题,但是在很多应用情况下,消声管道沿气流方向的截面是均匀一致的,此时可以将三维声学计算问题简化为二维声学问题。这时,消声管道的传递损失可以表示为与轴向波数有关的表达式,而轴向波数可以通过计算截面的特征值得到。
本文对消声管道的声学性能计算进行简化处理并使用两种简化方法:(1) 对简单规则截面结构形式使用基于传递矩阵的方法计算特征值。需要指出的是,传统的传递矩阵法[7]应用于沿介质气流方向(轴向)各个子结构的传递矩阵计算,本文在消声管道截面使用传递矩阵法,在一定的边界条件下得到特征方程用于计算特征值(也就得到了轴向波数)。(2) 对于复杂形式的截面特征值使用二维有限元方法进行计算,进而计算消声管道的传递损失。值得注意的是,二维有限元方法在文献[8–9]中被应用于消声器的声学性能预测:文献[8]将二维有限元方法与模态匹配法结合形成数值模态匹配法,结合管道截面变化处的边界条件形成一系列方程用于求解模态幅值系数;文献[9]将二维有限元方法与配点法结合,将管道内的声学量表示为半解析的形式,在选取的配置点处利用声压和质点振速的连续条件得到进出口的模态幅值系数。与上述文献不同,本文直接使用二维有限元法得到截面特征值用于传递损失的计算,将三维问题简化为二维问题以提高计算效率。通过与文献中的实验值及数值结果的比较验证了简化方法的有效性,并对考虑均匀流情况下的消声管道传递损失进行了预测。简化方法可以在保证计算精度的同时极大程度地提高计算效率,简化计算方法可用于管道消声系统的优化设计。
1 理论基础
通常情况下,消声管道在进出口处存在截面变化,因此三维数值方法常被用于管道内部声场的计算,虽然三维方法计算精度高,但计算效率较低,给实际的工程应用带来很大困难。本文在计算中忽略了进出口截面变化的影响,将三维声传播问题简化为二维问题,并通过实例说明这种简化假设在实际应用中是可行的。
对于如图1 所示的包覆式消声管道,可以使用基于传递矩阵的方法计算传递损失;如果结构截面形式较为复杂,即对于更一般的情况无法直接应用传递矩阵法时,可以使用二维数值方法(如有限元方法)进行计算。
1.1 等截面消声管道传递损失计算公式
对于一定长度的等截面消声管道,传递损失可以根据式(1)计算得到[10]:
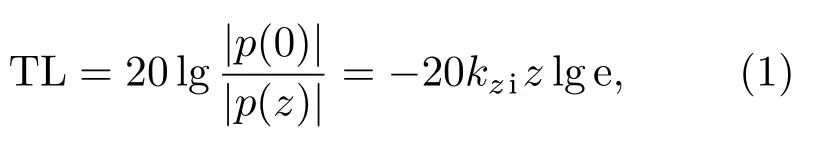
其中,p(0)和p(z)分别为相对位置为0 和z处的声压值,kzi为轴向波数的虚部,z为管道长度,e 为自然对数的底。可以发现,在等截面情况下,管道的传递损失可以通过计算轴向波数得到,值得注意的是,公式(1)是在无限长管道假设条件下得到的,因此对于长管道有更好的适用性。
1.2 管道消声性能计算的传递矩阵法
传递矩阵描述了管道进出口声压和质点振速的关系,可以表示为

其中,T为传递矩阵,pI和pO分别为进出口的声压,uI和uO分别为进出口的质点振速。
对于如图1 所示的包覆式消声管道,如果忽略矩形管道截面边角的影响,可以分别考虑x和y两个方向的传递矩阵关系,在y方向,吸声材料及空气中的传递矩阵分别表示为

其中,ky和分别为空气和吸声材料中y方向的波数,ρ0和分别为空气和吸声材料的密度,ty为吸声材料y方向厚度,h为空气域厚度,i 为虚数单位,ω为圆频率。穿孔板内外两侧的传递矩阵可以表示为

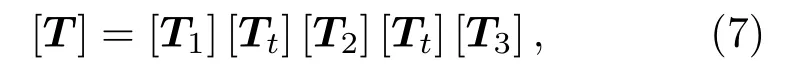
即为

图1 方形包覆式消声管道Fig.1 Square silencing duct with packed housing

根据位置1 和位置4 处的刚性壁边界条件,得到t21=0,即为y方向的特征方程。
同理,使用同样的方法可以得到x方向的特征方程。求解由两个特征方程构成的方程组即可求得两个方向的波数kx和ky,轴向波数可以通过式(9)计算得到:

将轴向波数代入式(1)即可得到传递损失。
对于圆形截面包覆管道,如图2 所示,ri和ro分别为穿孔管内侧空气域半径以及管道半径,空气中的声压和质点振速可以分别表示为
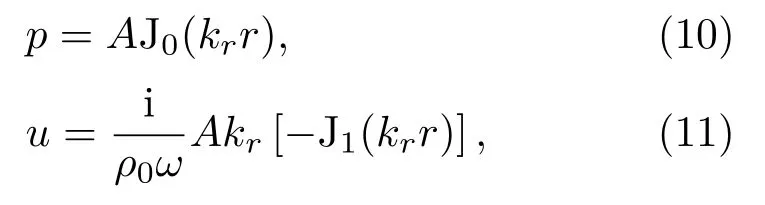
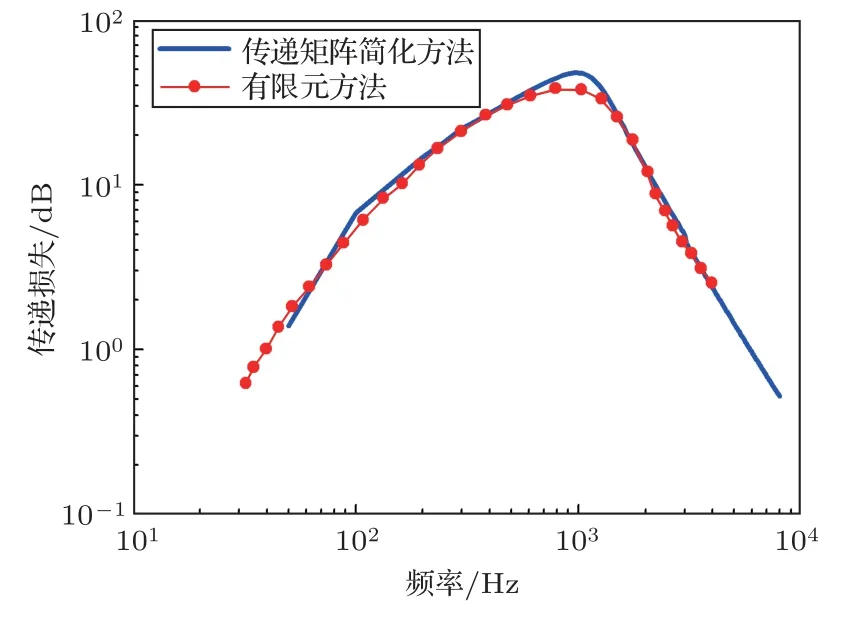
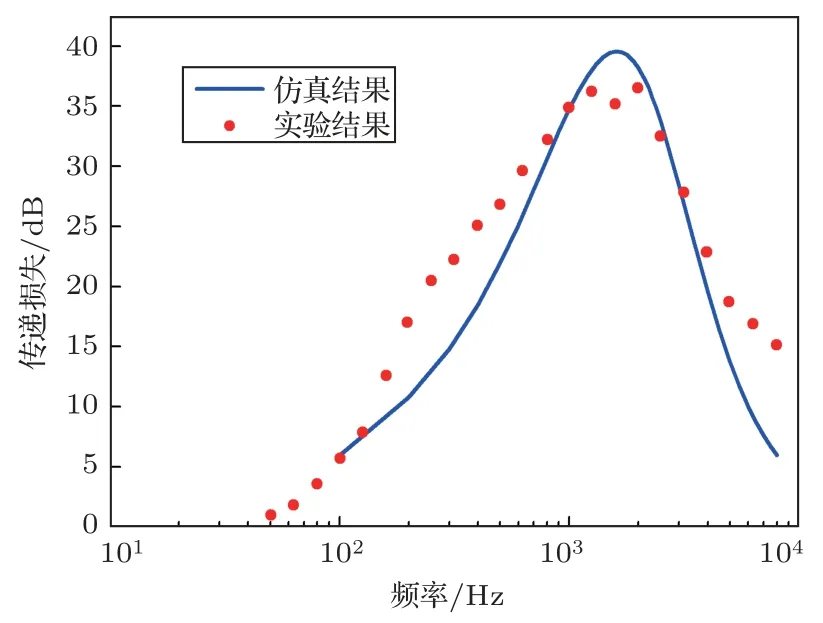
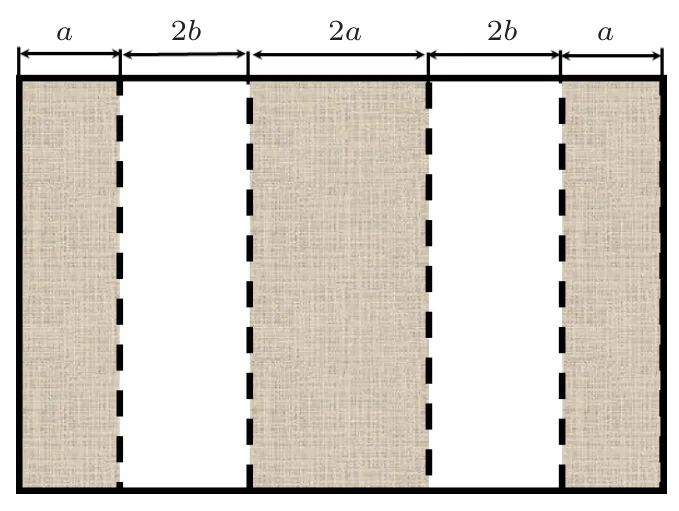
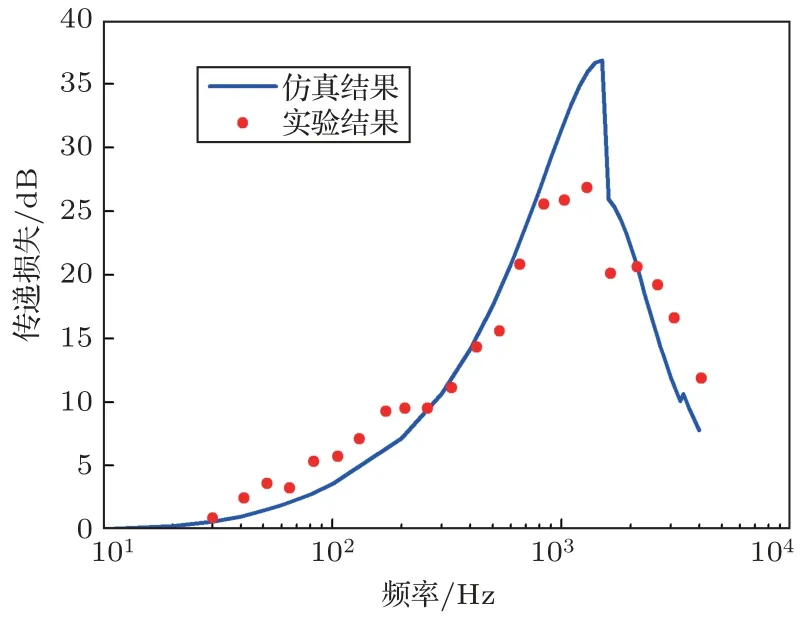
其中,A为模态系数,ρ0为空气密度,kr为横向波数,J0和J1分别为0 阶和1 阶第一类贝塞尔函数,0r 其中,B和C为模态系数,为吸声材料的密度,为吸声材料中的横向波数,Y1为第二类1 阶贝塞尔函数,rir 图2 圆形包覆式消声管道Fig.2 Round silencing duct with packed housing 穿孔管处以及管道外壁的边界可以分别表示为 将声压以及质点振速表达式代入边界条件得到如式(15)的方程组,求解方程组并利用波数关系式(16)得到轴向波数进而计算传递损失。 求解行列式等于0 的特征方程可以得到kr,轴向波数kz可以通过下式得到 需要指出的是,传递矩阵法中只考虑了管道中平面波传播的情况,没有考虑高阶模态的影响。 传递矩阵法的计算效率较高,但是对于更一般的情况,如果截面形式较为复杂,无法使用传递矩阵法,这时可以考虑使用二维数值方法计算轴向波数,本文使用的是二维有限元方法。 空气域和吸声材料域如图3 所示,两个区域通过穿孔边界连接,在空气域考虑存在均匀流,空气和吸声材料中的二维声波控制方程为 空气和吸声材料中等效的横向波数kxy1和kxy2分别满足以下方程: 其中,M为马赫数。 图3 非规则消声管道截面示意图Fig.3 Cross-section of non-regular silencing duct 消声管道的边界条件为刚性壁面边界条件和穿孔阻抗边界条件,应用伽辽金加权余量法以及格林公式可以得到横截面C1和C2上的横向本征方程为[11] 其中, 分别为横截面上的广义刚度矩阵、质量矩阵和穿孔阻抗矩阵。N为形函数的列向量,p1和p2分别为横截面C1和C2上节点声压组成的列向量,角标“e”代表单元,Se为空气域或吸声材料域面单元,Le为穿孔边界线单元。 联立方程(21)和(22)可以得到考虑均匀流影响的消声管道的横向本征方程为 其中, 求解方程(23)即可以得到轴向波数,进而计算传递损失。 本节将通过若干算例验证基于传递矩阵法和二维有限元法的两种简化方法的合理性,说明简化计算方法在实际工程问题中的应用价值。 首先对一个如图1所示的方形包覆式消声管道进行消声量的计算,管道外尺寸为0.6 m×0.6 m,吸声材料厚度0.1 m,管道长度2 m,吸声材料为岩棉,其流阻率为31500 Rayl/m,穿孔板厚度为0.7 mm,穿孔直径为3 mm,穿孔板穿孔率为33%,穿孔阻抗公式来源于文献[9]。基于传递矩阵的简化方法与文献[11]中有限元方法的比较如图4 所示,二者趋势吻合较好,说明对于包覆式方形管道,边角对其声学性能的影响较小,本文1.2 节中的简化处理较为合理。传递矩阵法的计算效率高,具有一定的应用价值。 图4 方形包覆消声管道消声量Fig.4 TL of a square packed silencer 考虑一个方形Bar 消声器(此处命名为消声器a),结构截面如图5 所示,消声器外壳尺寸为0.6 m×0.6 m,Bar 尺寸0.4 m×0.4 m,管道长度2 m,吸声材料参数及穿孔率与上例包覆消声管道算例相同。使用二维有限元简化方法计算传递损失,仿真结果与实验结果[12]比较如图6 所示,二者在宽频范围内吻合较好,说明了基于二维有限元的简化方法的正确性。 图5 方形Bar 消声器截面形式Fig.5 Cross-section of the square Bar silencer 考虑文献[11]中的另一个Bar 消声器(此处命名为消声器b),与消声器a 不同的是外壳尺寸为0.6 m×0.8 m,Bar的尺寸以及其它参数与消声器a相同。使用二维有限元方法计算传递损失的仿真结果与实验值[11]对比如图7 所示,仿真结果同样较好地预测了消声管道的声学性能。 第三个算例为如图8 所示的圆形Bar 消声器,包覆吸声材料的圆形管道内部包含一个圆形的Bar,尺寸为r= 0.1 m,R= 0.291 m,t= 0.147 m,管道长度L= 0.9 m,穿孔板穿孔率为27%,穿孔孔径3 mm,穿孔板厚度1.6 mm,穿孔阻抗公式及吸声材料特征参数与文献[9]中相同。特征值使用有限元方法计算得到,管道传递损失计算结果如图9所示,除了极高频附近频段,仿真预测结果与实验值[9]在宽频范围内吻合较好。 图7 Bar 消声器b 传递损失对比Fig.7 TL comparison of bar silencer “b” 图8 圆形Bar 消声管道截面Fig.8 Cross-section of round Bar silencing duct 图9 圆形消声管道传递损失与实验值对比Fig.9 TL comparison of round Bar silencing duct 消声管道作为介质传输的路径,介质存在流动速度,流速对管道的声学性能具有一定的影响,本节考虑两个均匀流情况下的消声管道传递损失计算,说明方法在这种情况下的适用性。 第一个算例为一个片式消声器,结构截面如图10 所示,结构尺寸为a= 0.1 m,b= 0.1 m,管道长度为1.8 m,穿孔率27%,穿孔孔径3 mm,吸声材料流阻率为1881 Rayl/m,穿孔阻抗以及吸声材料特征参数公式与文献[9]一致。管道内流速马赫数为0.022。仿真结果与实验值[13]对比如图11 所示,在极高频处预测结果存在一些偏差,但总体来说二者的趋势整体吻合较好,说明了本文仿真方法的正确性。 图10 片式消声管道截面形式Fig.10 Cross-section of a splitter silencer 图11 有流情况下方形片式消声管道传递损失与实验值对比Fig.11 TL comparison of square splitter silencer with uniform flow 第二个算例为一个Bar 消声器,Bar 尺寸为0.4 m×0.4 m,外壳尺寸为0.6 m×0.6 m,气流速度40 m/s,管道长度为2 m,吸声材料流阻率为31500 Rayl/m,穿孔率33%,穿孔孔径5 mm。仿真结果与文献[11]中实验值对比如图12所示,仿真结果较好地描述了消声管道的声学性能,进一步说明了计算方法的正确性。由于简化方法将三维数值计算转化为二维数值计算,将极大程度地提高计算效率。 图12 均匀流(40 m/s)情况下方形Bar 消声器传递损失Fig.12 TL comparison of Bar silencer with uniform flow 40 m/s 声学性能的快速准确计算对于消声管道的设计具有重要意义。传统三维数值方法计算量较大,计算效率低。由于消声管道一般具有沿轴向(气流)方向截面均匀一致的特点,此时管道的声学性能可以通过轴向波数进行简化计算,轴向波数可以通过对管道截面进行特征值分析获得。针对不同的消声管道结构形式,本文使用两种简化方法:基于传递矩阵的简化方法和基于二维有限元的简化方法,通过与文献中的数值结果和实验结果的比较说明了简化方法可以在较宽的频率范围较好地描述管道的消声性能,说明了简化方法的有效性。另外,简化方法也可以考虑管道内介质存在均匀流速的情况。简化方法将三维声学计算问题转化为二维声学问题,极大程度地提高了计算效率,可用于消声管道的快速优化设计。




1.3 管道消声性能计算的二维有限元方法
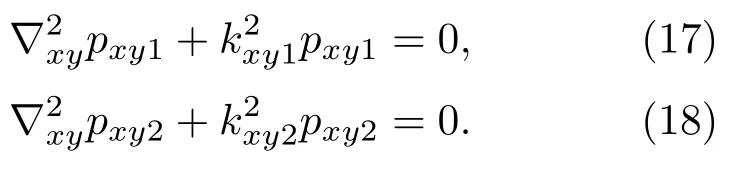



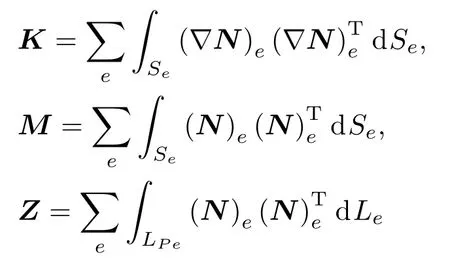
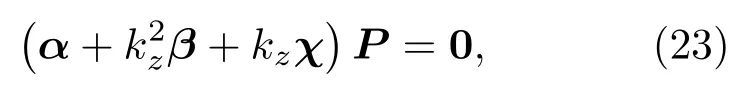


2 算例验证
2.1 无流情况包覆式消声管道
2.2 无流情况Bar消声器



2.3 均匀流情况消声管道的声学性能

3 结论

