Mg-Nd-Zn-Zr 稀土镁合金无缝管材正反挤压过程模拟

郑兴伟，赵宗，汪伟，殷浩浩

（1.上海海洋大学 工程学院，上海 201306；2.东华大学 理学院，上海 201620）

轻量化设计正成为汽车、高速列车、飞机等运输系统降低油耗和废气排放的有效解决方案[1—3]。镁合金具有密度低、比强度高、铸造性好、可加工性好等优良特性[1]。采用镁合金替代上述领域的铝合金或钢结构件，可以有效实现减重。无缝管材是运输系统中一个重要而广泛应用的部件，开发低成本、高强度和耐腐蚀的镁合金管材，替换交通运输系统中传统的钢铁和铝合金无缝管材具有十分重要的意义。

由于镁合金无缝管材的应用潜力较大，无缝管材的制备技术是镁合金研究领域的一个热点。近些年该领域也取得了较大进步，一些高质量的AZ31，AZ61，AZ80 和ZK60 镁合金管材制备工艺已经被成功开发[4—5]，同时针对相应镁合金管材制备过程的有限元仿真也开展了大量研究[6—7]。截至目前为止，针对稀土镁合金无缝管材制备过程的有限元仿真相关报道却很少涉及。文中以新型 Mg-3%Nd-0.4%Zn-1%Zr（NZ30K）合金的无缝管材制备过程为研究对象，系统开展模具结构优化和正反挤压过程的有限元研究，为该镁合金的无缝管材制备提供技术基础。

1 无缝管材挤压过程有限元仿真方法和模型

1.1 正挤压和反挤压的有限元模型

在实际实验过程中，正反挤压的凸模及凹模都采用耐热高强度的模具钢制造，图1 和图2 分别为正反挤压示意图。文中所采用的挤压温度在300～500 ℃之间，因此可以认为凸模及凹模为刚性体，建模过程将凸模以及凹模简化成两条刚性的线（不可变形），可以在保证精度的前提下简化模型和节约计算时间；另外一方面由于管材属于旋转对称体，因此只需要计算出某一个纵截面的物理场变化趋势，就可以反映整个过程中三维空间物理场的变化趋势，所以为了节约计算时间，反正挤压过程都简化成二维模型。

通过以上分析且结合实际实验，正反挤压过程的有限元模型如图3 和图4 所示，可以发现两个有限元模型都是由两个模具（凸模和凹模）、对称轴以及变形坯料4 部分构成。另外在反挤压模型中，由于凹模和坯料都属于旋转对称体，结构的优化对挤压过程的应变场、流动场和温度场的影响相对较小，而反挤压主要依靠凸模推动坯料成形，因此凸模外形的设计对反挤压过渡产品质量有着至关重要的影响。同理正挤压主要通过凸模推动坯料，经过凹模的工作带迫使坯料成形，因此正挤压模具的挤压角（见图1）、润滑条件以及挤压温度对最终管材的质量影响较大。

1.2 力学模型

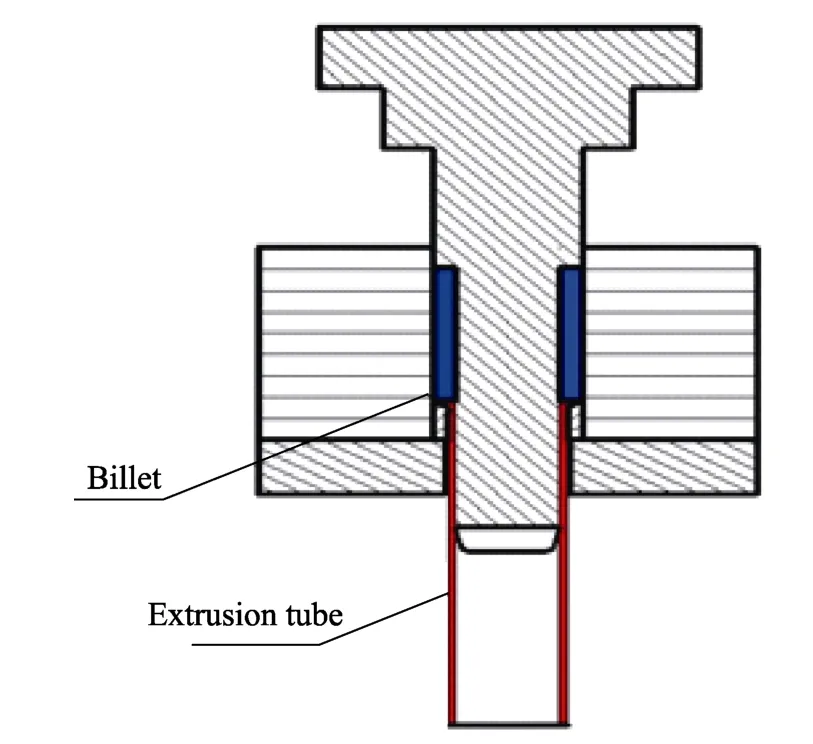
图1 正挤压示意图Fig.1 Forward extrusion diagram

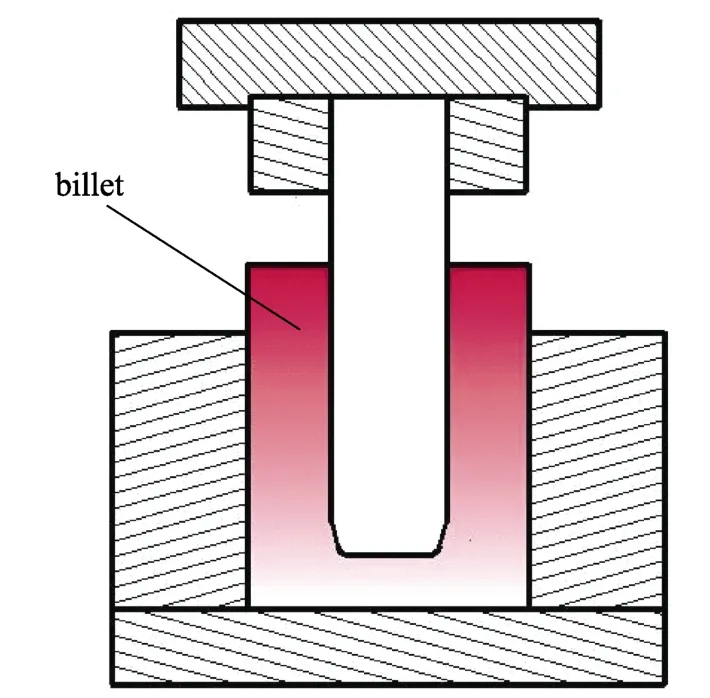
图2 反挤压示意图Fig.2 Backward extrusion diagram

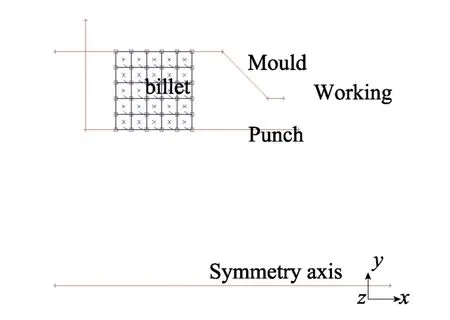
图3 正挤压有限元模型Fig.3 Finite element model of forward extrusion

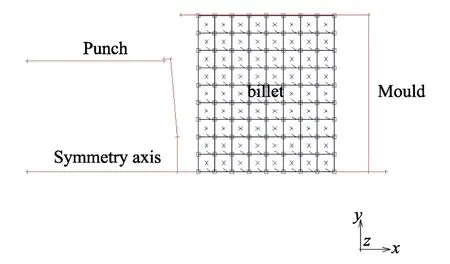
图4 反挤压有限元模型Fig.4 Finite element model of backward extrusion

目前商业化软件MSC.SUPERFORM 可以提供两种不同的变形有限元单元：弹塑性有限元法和刚塑性有限元法。弹塑性有限元理论认为，材料在变形过程的总应变ε分为弹性应变eε和塑性应变pε两部分，eε为卸载后可以消除的应变，pε为卸载后无法消除的应变。应力-应变服从下述规律[8]：

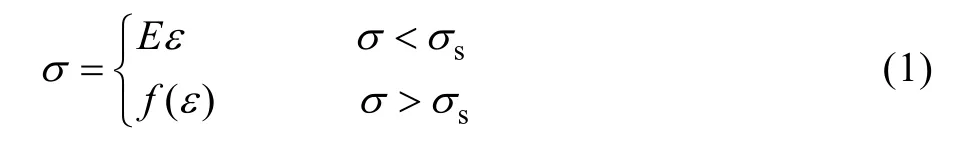
式中：E为弹性模量；σs为弹性屈服极限。

由于反挤压和正挤压变形两个过程累积的塑性变形量很大，弹性变形可以忽略，因此文中采用效率比较高的刚塑性有限元进行模拟计算。根据刚塑性有限元理论，对材料做如下假设：①忽略材料的弹性变形、体积力及惯性力的影响；② 材料均质且各向同性，体积为不可压缩的连续体；③材料的变形流动服从Levy-Mises 流动理论；④ 加载条件（加载面）给出刚性区与塑性区的界限。

1.3 材料参数

采用有限元法模拟金属塑性变形时，材料的物性参数是否准确是决定塑性变形模拟结果的一个重要因素。目前版本的SUPERFORM 软件只有常见钢铁和铝合金的数据库，而镁合金的数据库几乎没有涉及，因此变形过程的物性参数需要自己测定或者近似替代。挤压模拟过程所选取的NZ30K 合金物性参数如表1 所示。文中NZ30K 合金的力学性能采用本章前半部分所建立的本构方程式输入。

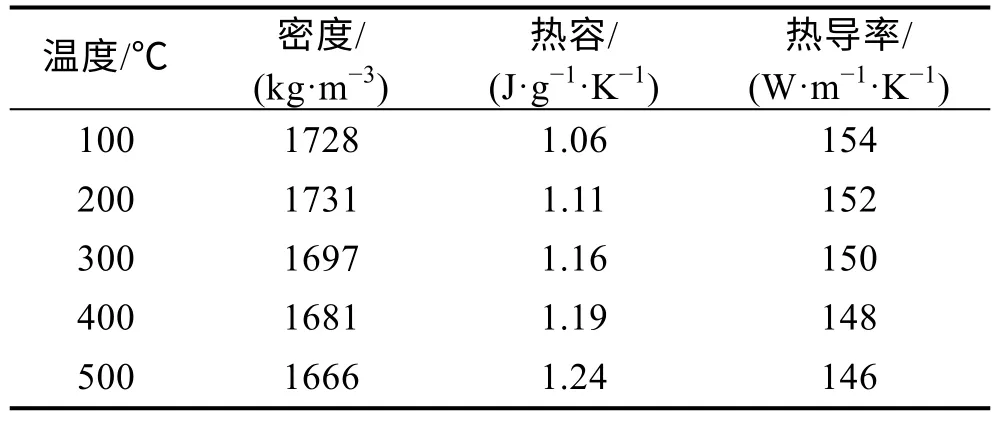
表1 变形模拟所采用的NZ30K 合金物性参数Tab.1 Physical properties of NZ30K alloy applied in deformation simulation

2 结果与讨论

2.1 挤压模具结构仿真

挤压过程坯料的流场不仅对成形产品的质量有影响，而且对挤压成形过程需要的挤压力大小也有直接关系。文中反挤压和正挤压模具都属于旋转对称体，正反挤压模具主体设计相对简单，因此本优化主要考虑凸模圆角大小以及正挤压模具的挤压角对大管材挤压成形过程流场以及应变场的影响。

2.1.1 反挤压凸模圆角对流场和应变场影响规律

反挤压模具、凸模圆角半径R分别为0（即采用直角凸模），10，20 mm 时，NZ30K 合金在400 ℃条件下凸模运动到距凹模底部10 mm 时的反挤压流场见图5。从图5a 可以发现，当凸模圆角半径为0 mm时，反挤压时坯料流动方向沿着垂直反挤压凹模内壁方向，因此在反挤压过程对挤压模具有很大向外扩张的冲力，会严重影响模具的寿命。

从图5b—c 可以发现，当反挤压模具凸模圆角半径分别为10 mm 和20 mm 时，挤压过程金属坯料的流场发生了明显变化。相对于直角凸模挤压过程坯料流场，金属坯料流动的方向逐渐转向平行于反挤压凸模方向，因此反挤压凸模采用一定圆角半径之后，反挤压模具受到垂直于内壁方向的扩张力也随之减少，向外扩张力的减少对提高模具寿命有着重要的意义。另一方面，对比过渡半径为10 mm 和20 mm 两个凸模进行挤压时的坯料流场可以发现，两个不同圆角半径的挤压凸模对金属坯料流场几乎没有影响，但是随着圆角半径的增加对凸模本身的寿命却带来了一定的负面影响，同时随着凸模圆角半径的增加，反挤压之后需要切除的反挤压坯料也会随之增加。综上可知，采用半径为10 mm 的凸模时，不仅不会影响凸模的寿命，而且可以获得相对较优的流场。

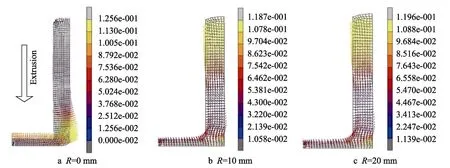
图5 凸模圆角半径对流场的影响Fig.5 Effect of punch radius on flow field

挤压应变分布是表征挤压型材质量的一个重要参数，挤压应变分布越均匀，则挤压管材的残余应力越小，特别是需要再次挤压变形的过渡坯料，挤压应变分布不均匀对后续挤压会产生不利的影响。凸模圆角半径分别为0（也就是采用直角凸模），10，20 mm时，反挤压之后的应变分布见图6，可以发现采用直角凸模挤压成形的反挤压坯料应变分布最不均匀，而采用过渡半径为10 mm 和20 mm 时，反挤压之后坯料内部的应变场变得相对均匀，其原因可以归结于采用一定挤压角后，反挤压过程坯料的流动方向得到了改善；另外一方面，应变场的改善有利于减少后续正挤压过程中裂纹、毛刺等缺陷的产生。

为了验证增大凸模圆角半径对挤压过程金属流场的改善作用，文中用SUPERFORM 软件对以上几种圆角半径的凸模进行反挤压时所需挤压力的大小进行预测，具体预测结果如图7 所示。可以发现，挤压力随着圆角半径的增加而减少，这一结果与采用圆角凸模会改善反挤压过程金属坯料流场的结论一致。同时可以发现，3 个不同圆角半径的凸模在整个反挤压过程中的挤压力都可以分为两个部分：①挤压力随着凸模位移的增加而增加，这一部分对应的是镁合金坯料弹性变形过程；② 当凸模位移超过挤压坯料弹性变形极限后，挤压力并没有随着位移的增加而增加，而是保持几乎不变或者稍微有点下降。这一结果说明达到弹性变形极限之后，NZ30K 合金在400 ℃进行反挤压变形时，加工硬化和再结晶软化达到了动态平衡。

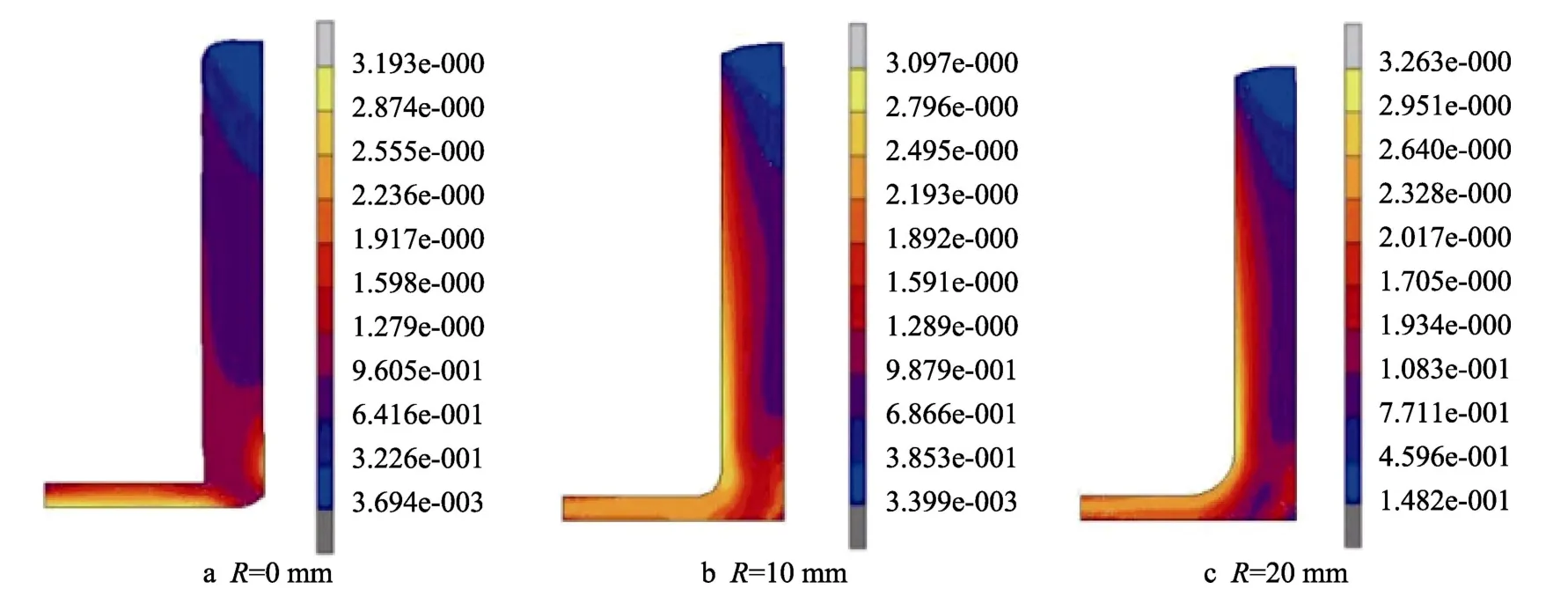
图6 凸模圆角半径对应变场的影响Fig.6 Effect of punch radius on strain field

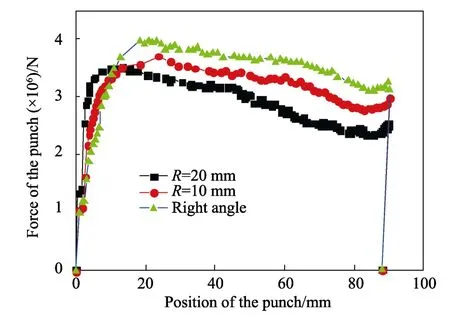
图7 凸模挤压角对挤压力的影响Fig.7 Effect of punch extrusion angle on extrusion load

2.1.2 正挤压挤压角对流场和应变场影响规律

图8 为正挤压模具的挤压角分别为0°，30°，45°，60°时，NZ30K 合金在400 ℃条件下凸模运动到距凹模挤压角5 mm 时的流场分布。从图8a 可以发现，当挤压角为0°时，挤压管材的表面出现了明显的凹凸不平，而且最大流速方向沿着凸模径向，因此会大大增加挤压力和对凹模的扩张冲力。从图8b—d 可以发现，随着挤压角的增加，不仅金属坯料的流场得到明显改善，而且挤压成形之后表面粗糙度也得到了明显改善；另一方面，随着挤压角的增加，模具的清理也变得更加容易，但是随着挤压角的增大会导致残留在模具过渡区域的镁合金量也会增加，以及模具整体高度增加进而导致模具成本增加。

图9 为正挤压模具挤压角分别为0°，30°，45°，60°时挤压管材应变量的分布。从图9 可以发现，当正挤压模具挤压角为0°时，挤压成形的管材出现了局部应变集中，从而容易导致在成形管材中出现裂纹缺陷。随着挤压角的增大，挤压管材的应变分布变得越来越均匀，尤其是当挤压角为60°时，挤压管材除过渡区之外的应力分布都十分均匀。

图10 为正挤压挤压角分别为0°，30°，45°，60°时正挤压过程的挤压力大小的模拟结果。从图10 可以发现，当挤压角为0°时，正挤压变形初期所需的外加力随着变形量急剧增加，同时在变形后期，随着变形量的增加，材料发生了明显的加工硬化，过渡区内金属的流动变得越来越困难，因此挤压力在变形末期出现了一个明显峰值。当挤压角为30°，45°，60°时，由于过渡区的缓冲作用，挤压初期外加力的增加明显变得更加缓和，而且消除了挤压变形过程最后阶段应力急剧增加的不良影响，而且整个挤压过程的挤压力也有所下降。

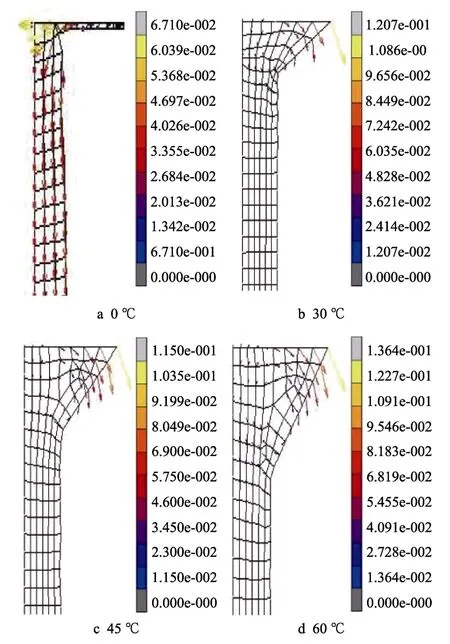
图8 不同正挤压模具挤压角对流场的影响Fig.8 Effect of different extrusion angle of forward extrusion die on flow field

综上发现，挤压角对挤压过程的流场影响最大，随着挤压角由0°增加到30°，挤压力明显下降。主要是由于有一定挤压角后，正挤压过程金属从模具腔体流入过渡区的方向由最初垂直于挤压方向转变成和挤压方向约为30°夹角的方向；另外一方面，随着挤压角的增加，挤压管材的表面质量也有所提高，并且应变分布也更加均匀，但是挤压角的增加也会带来一定的负面影响，主要表现在过渡区的残余坯料增加以及模具高度的增加，从而提高了模具的成本。综合以上模拟结果，文中认为挤压角为30°最优。

2.2 挤压工艺参数对流场和应变场影响规律

挤压工艺参数主要包括变形温度、变形速度以及变形过程采用的润滑条件。合理的工艺参数不仅可以提高管材的合格率，而且可以改善管材的显微组织。已有研究表明，挤压速度对流场以及宏观应变分布几乎没有影响[9]，因此文中并没有对挤压速度展开详细的讨论。

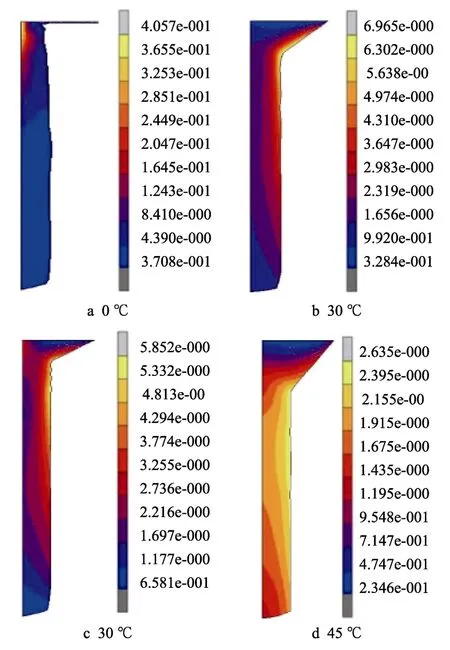
图9 不同正挤压挤压角对应变场的影响Fig.9 Effect of different forward extrusion angle on strain field

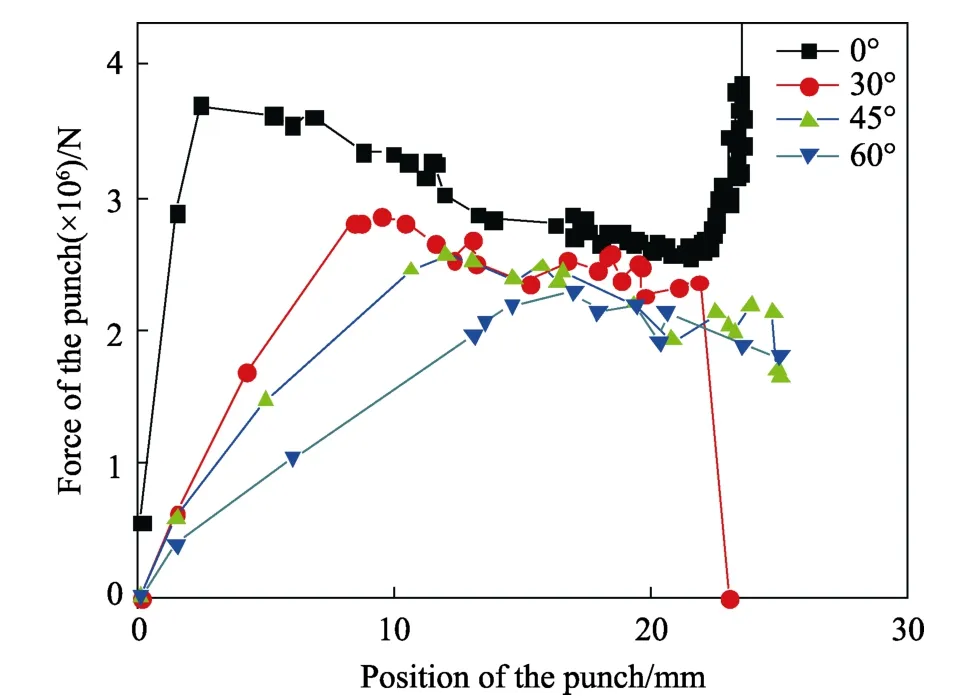
图10 挤压角对挤压力大小的影响Fig.10 Effect of extrusion angle on extrusion load

2.2.1 挤压温度对流场应变场影响规律

图11 为挤压温度分别为300，350，400，450，500 ℃条件下管材应变分布，可以发现随着挤压温度的提高（特别是挤压温度从300 ℃升高到400 ℃时），挤压管材的应变分布越来越均匀。可能原因是：NZ30K 合金的挤压温度低于400 ℃时，挤压过程加工硬化效果大于软化效果，即合金没有发生完全再结晶，因此挤压之后只有局部的应力得到释放，而当挤压温度超过400 ℃时，挤压过程已经发生了完全再结晶，挤压过程的应力和应变得到了释放，因此挤压温度的提高有利于应变的均匀化。

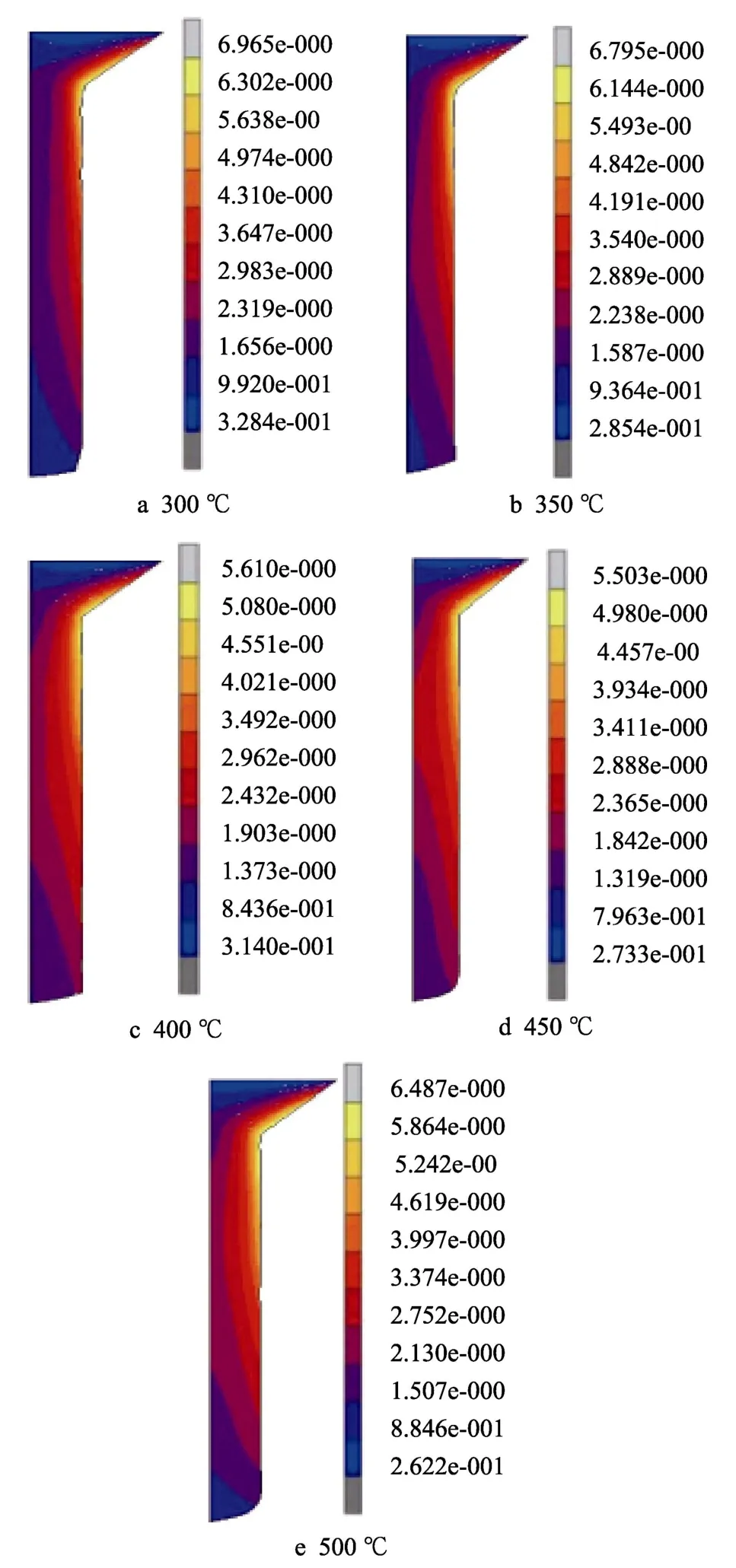
图11 挤压温度对应变场的影响Fig.11 Effect of extrusion temperature on strain field

图12 为挤压温度分别为300，350，400，450，500 ℃时，正挤压过程所需要挤压力模拟结果，可以发现随着变形温度的提高，挤压力随着变形温度的提高而降低。这是因为随着挤压温度升高，镁合金变形的临界应力在逐渐下降。综上考虑挤压过程的流场、挤压应变分布以及挤压力可知，NZ30K 理想的变形温度在400 ℃左右，这一模拟结果和本章前半部分的拉伸和压缩热模拟确定的NZ30K 适宜变形温度正好吻合。

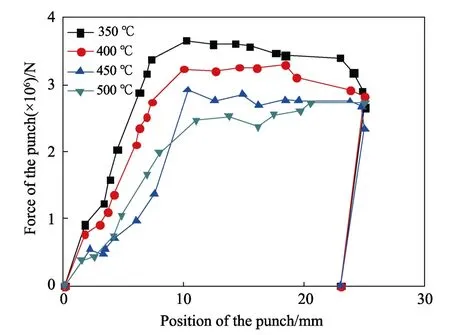
图12 挤压温度对挤压力的影响Fig.12 Effect of extrusion temperature on extrusion load

2.2.2 摩擦对应变场和挤压力的影响规律

润滑条件影响挤压管材表面质量同时也会影响挤压力。图13 为摩擦因数µ分别为0，0.2，0.5，1条件下，进行挤压时管材的应变分布模拟结果。模拟结果表明，摩擦因数对挤压管材表面应变分布有较大的影响，摩擦因数越小，所影响的深度越小，这是因为摩擦力作用的物体表面与挤压运动方向相反的力学本质是相互吻合的。

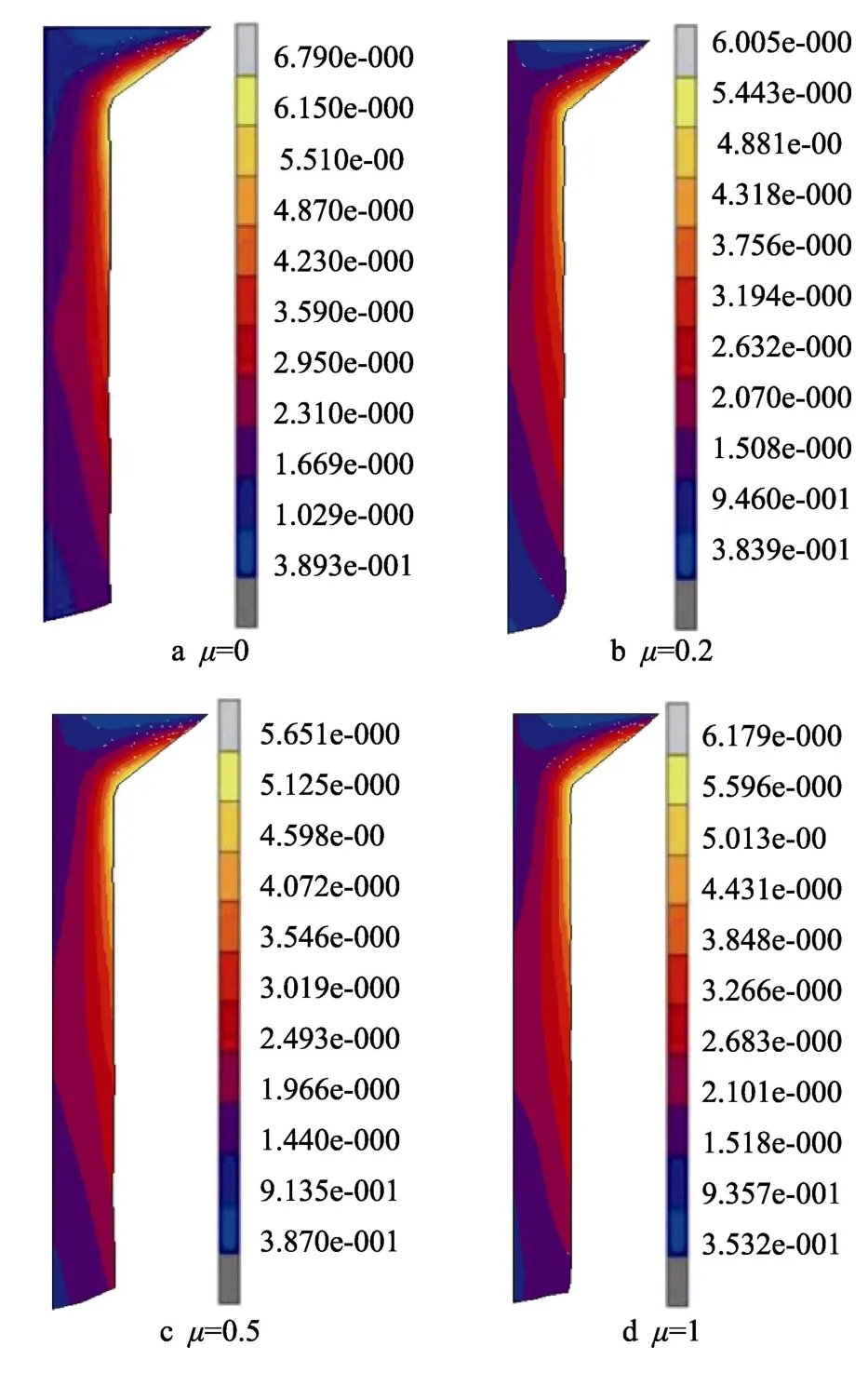
图13 摩擦因数对应变量场的影响Fig.13 Effect of friction coefficient on strain field

图14 为摩擦因数为0，0.2，0.5，1 条件下，进行管材挤压所需挤压力的模拟结果。模拟结果表明，随着摩擦因数的提高，实际挤压过程所需要的挤压力越大，但是两者并不呈正比例变化。这是由于在挤压过程中，挤压力需要克服两个力：摩擦的外部力以及坯料变形所需的内部力，在其他条件不变的前提下，坯料本身变形所需的力不变，仅仅是提高了克服摩擦力这一部分，因此挤压所需的外加力不是随着摩擦因数线性增加。

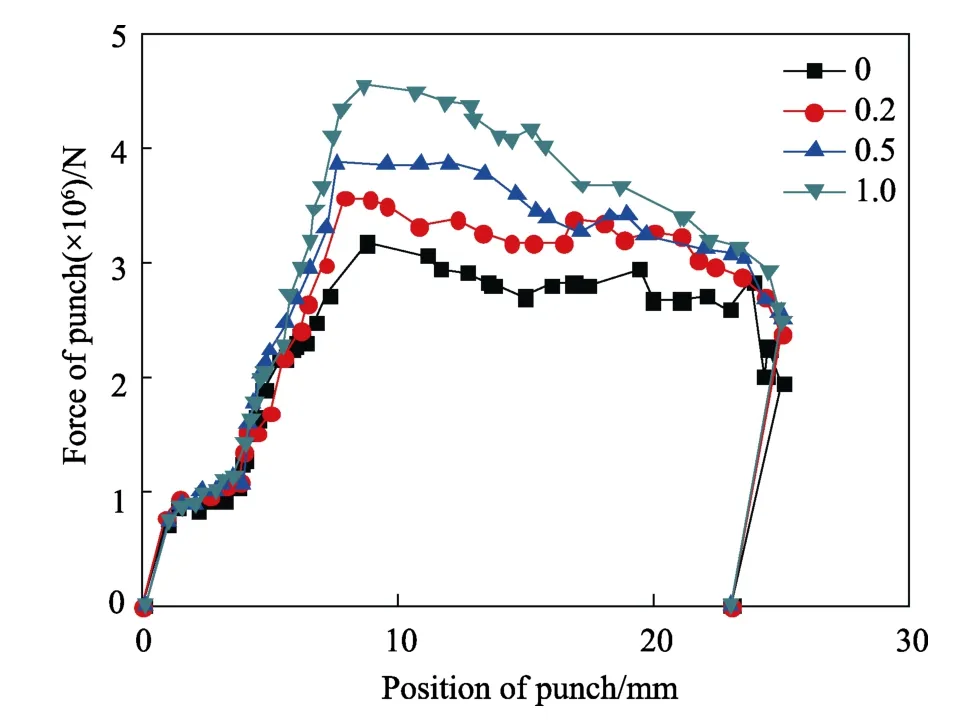
图14 摩擦因数对挤压力的影响Fig.14 Effect of friction coefficient on extrusion load

3 结语

1）对稀土镁合金无缝管材正反挤压过程进行模拟，当反挤压凸模圆角为10 mm 时不会影响凸模寿命，而且可以获得相对较优的流场；正挤压挤压角为30°时，应变分布均匀，挤压力最低。

2）稀土镁合金无缝管材在不同挤压温度和摩擦因数模拟结果表明，挤压温度对流场影响不大，随着挤压温度提高，应变分布越来越均匀；挤压力随着挤压温度升高而逐渐下降，NZ30K 合金适宜的挤压温度为400 ℃；摩擦因数越大，实际挤压过程所需要的挤压力越大。