一类被积函数为sin(x2)的积分问题研究

廖春艳 王梦丹

（湖南科技学院 理学院，湖南 永州 425199）

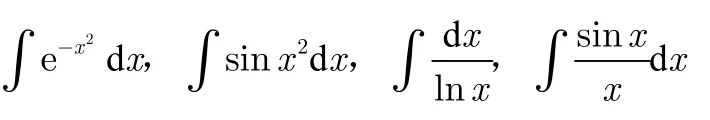
1 问题及其求法

1.1 利用积分第二中值定理求解

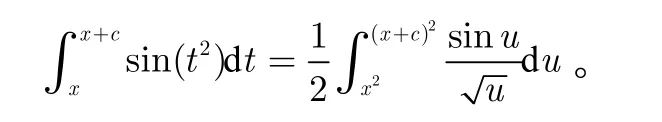
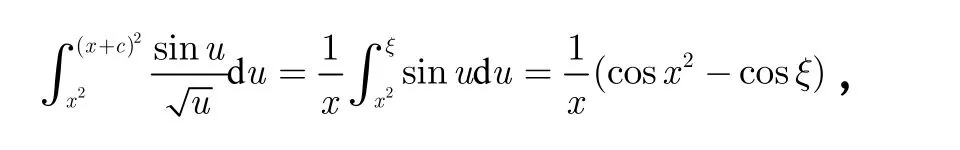
于是有 得证。

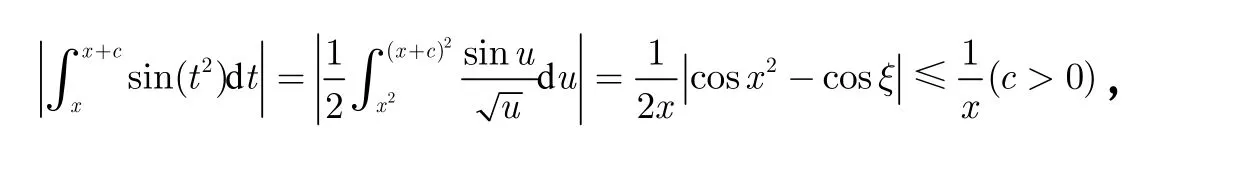
本例是利用积分第二中值定理来证明这个不等式，我们也可以利用类似的方法来证明一些被积函数为三角函数 sin(x2)的积分等式。

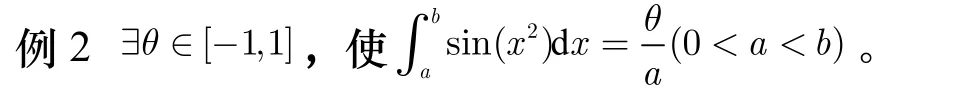
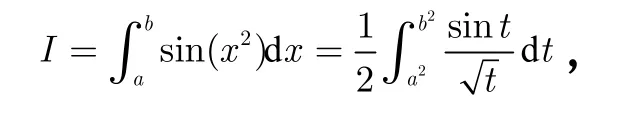
由积分第二中值定理，存在 ξ ∈ [a2, b2]，使得

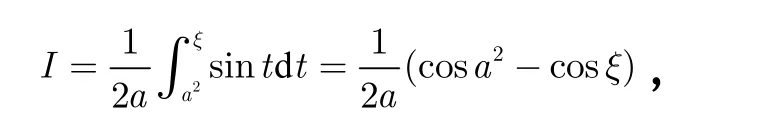
1.2 利用定积分的性质及分部积分法求解

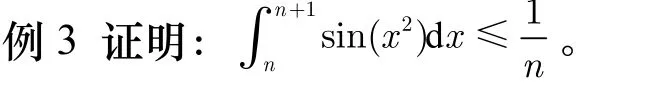
分析，本题的类型和例1 是类似的，只是上下限的形式有点不同，可以考虑用积分第二中值定理来求解，同学们可以自行证之。在这里我们换一种方法来进行求解。

解：由分部积分法，有

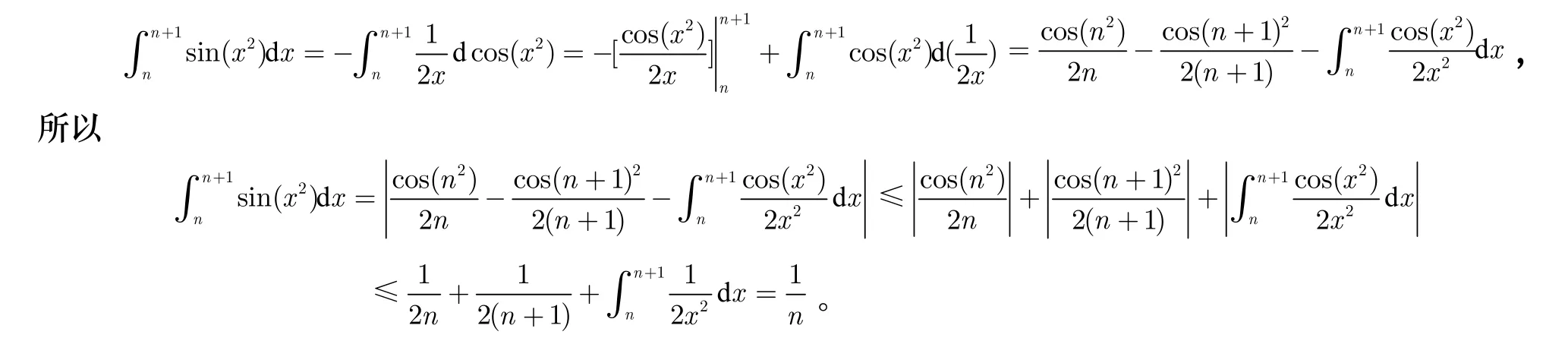
本例我们利用分部积分和定积分的性质来进行求解，解题过程也是非常直观的，也容易被同学接受。同学们看到定积分，想到最多的就是利用分部积分法和换元法进行求解。

1.3 利用积分式变换求解

下面我们利用定积分的换元法来解决下面例题。

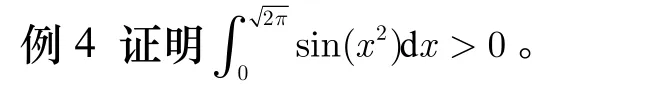
分析，本例我们还能不能用分部积分法来求呢？我们来看下，利用上例的方法不难得到

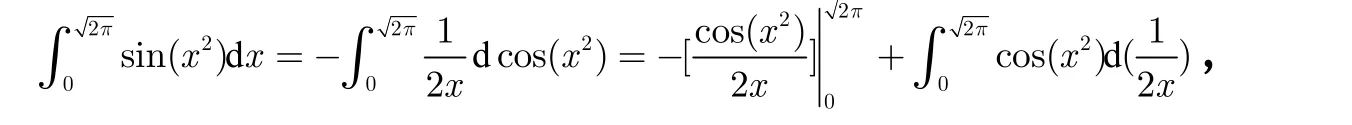
我们发现如果下限为0 的话，等式的前半部分是没有意义的，所以不能采用分部积分的方法来进行求解，我们换一种思路来考虑。

证明：令x2= y，则有

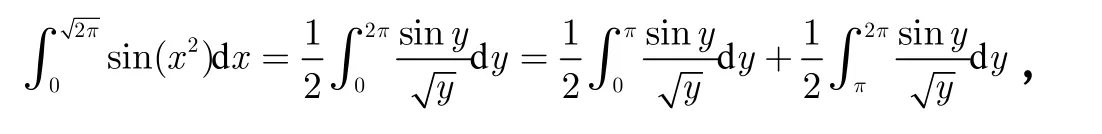
对第二个换元z = y − π，则有

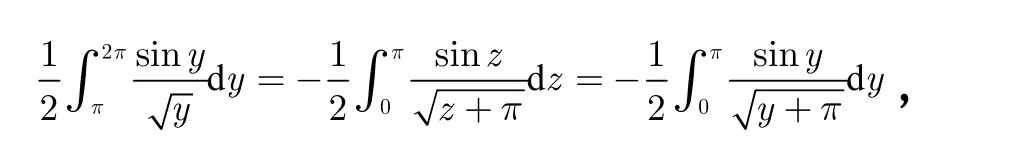
所以原积分就等于

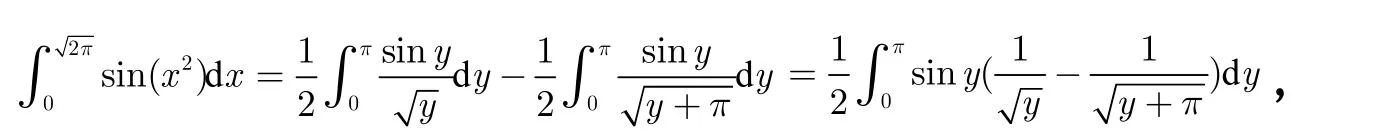
注：对于这类问题采用通常的积分方法，通过分部积分法或者直接换元法转换为求原函数的方法来计算定积分行不通，可以采取这种积分式变换的方法来得到问题的解。对于这类问题可以归结为原函数不能用初等函数表示求定积分问题，基本思路与方法差不多。一般通过拆分积分项的方法转换为原积分和一个数值，或者转换为两个可以互相消去的积分项和一个积分值来得到原积分的值。

下面我们利用上例的结论来判断下例积分的符号：

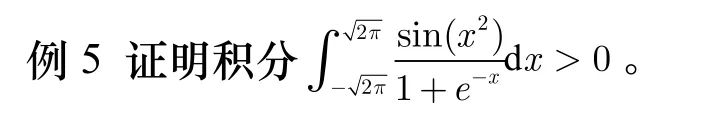
分析，这道题的被积函数并不是只有三角函数，同样，它的原函数我们很难去求解，怎么办呢？我们不妨观察下本例，这个积分的上下限是关于原点对称的，我们很快想到积分的对称性，但是很遗憾，被积函数并不具备奇偶性，所以本题的求解只能另辟蹊径。还是采用前面的方式，换元再拆分。

2 结 语

数学分析中涉及到三角函数的积分问题有很多，本文主要探究的是被积函数为sin(x)2的一类特殊的三角函数的积分等式及不等式问题，利用积分中值定理、分部积分法、换元积分法以及积分的性质，对原积分进行拆分、换元、求解。通过以上例题的分析，有利于理解数学分析中的一些被积函数含有三角函数的积分问题，在学习中发现新的知识，研究出新的求解规律。