套管压裂管柱安全性计算方法与准确性研究
(中国石油新疆油田分公司 工程技术研究院,新疆 克拉玛依 834000)
新疆油田公司采用了大型体积压裂工艺来提高玛湖和吉木萨尔油区的非常规油藏的渗透率。在实施大排量(达到14 m3/min)压裂时,为尽可能降低摩阻,使用油层套管充当压裂管柱是必然选择。在实际作业时,经常遇到施工泵压高和部分层段的起裂压力高等情况,井口泵压达到85~90 MPa,接近套管的抗内压极限。这对油层套管的安全性产生很大影响。因此,油层套管的管柱安全性计算对压裂施工有着重要的指导意义。只有合理地确定施工极限压力,才可以科学地指导压裂施工。
1 套管柱载荷分析及安全性计算方法
通常,油气井杆管柱的力学分析多采用Von Mises屈服准则[1]。这种基于静态受力分析的方法在压裂、完井领域的应用相当普遍[2-7]。在计算压裂管柱的安全性时主要考虑的载荷为管柱重力,管柱内外压差,温度变化引起的管柱长度改变及因此产生的附加应力[8]。
实际油气井中的油层套管的下端被固井水泥固定,上端通过卡瓦等装置固定在井口,属于两端固定的约束形式。压裂时,未固井段的套管除了承受自重力和压外压差之外,还承受着由于管柱“鼓胀变形”、“温度效应”产生的额外载荷,受载情况较下部已固井段的套管更加恶劣。因此,本文研究对象选为未固井段的油层套管。载荷可以分为轴向力、管柱内外压差2类。
1.1 轴向力分析
轴向力由3个力构成。
1) 管柱自重力产生的轴向力。油层套管柱的自重力从井口至井底逐渐递减,呈线性分布。因此,承受自重力最大的是井口处套管。自重力为:
FG=0.009 8Lm
(1)
式中:FG为未固井段油层套管的最大自重力,kN;L为未固井段长度,m;m为油层套管在空气中的线质量,kg/m。
估算套管重力时一般不考虑浮力影响[9]。此外,完井作业时,为防止套管柱在井内弯曲,一般在井口施加提升载荷,其值为未固井段套管自重力的1.1倍,再坐好井口设备,这部分载荷也计入管柱自重力。
2) 鼓胀效应产生的附加轴向力。未固井段的油层套管由于管柱内外压差作用,产生“鼓胀”变形,会导致管柱产生“缩短”的趋势。由于套管上下两端为固定约束,因此该变形会使管柱产生额外拉力。该拉力值为:
(2)
式中:Fg为鼓胀效应使管柱产生的轴向载荷,kN;μ为管柱的泊松比;Δpo为管柱外压力变化的平均值,MPa;Δpi为管柱内压力变化的平均值,MPa;D为管柱外直径,m;d为管柱内直径,m。
3) 温度效应产生的附加轴向力。由于压裂过程是将低温液体注入高温地层的过程,这一过程会对套管柱产生“降温作用”。受物体“热胀冷缩”物理规律的影响,套管柱也会产生一个“缩短”的趋势,同样受管柱约束形式的影响,套管会产生额外轴向拉力。该力为:
(3)
式中:Fw为温度效应引起的管柱载荷,kN;α为管材的线性膨胀系数(一般取1.2×10-5),1/℃;Δt为井筒内温度的变化差值,℃;E为管材的弹性模量(一般取216 000),MPa。
上述所有轴向力产生的轴向应力为:
(4)
式中:σr为轴向应力,MPa;Ft为由轴向载荷模型计算得到的轴向力,Ft=FG+Fg+Fw,kN;r0为管柱外半径,m;ri为管柱内半径,m。
此外,油层套管还可能承受弯曲应力和剪切应力,产生的原因是由于管柱螺旋屈曲,这一般发生在油气生产等“增温”过程,此时管柱受到的是压载荷。在实施压裂时,管柱以受拉载荷为主,管体不容易发生屈曲变形,因此上述公式没有考虑弯曲应力和剪切应力的影响。
1.2 内外压差载荷分析
内外压差即是管内的压裂施工压力与管外的地层压力之差值。高的内外压差会在管体上产生径向和周向2个方向的应力,其最大应力发生在管柱外表面。此时,径向和周向2个方向的应力计算式为:
σr=-pi
(5)
(6)
式中:σr为管体截面径向应力,MPa;σθ为管体截面周向应力,MPa;pi为压裂施工压力;po为压力管柱环空压力,MPa。
1.3 管柱三轴应力分析
根据以上受载分析,压裂作业时油层套管可能发生的失效形式为管体断裂、节箍脱扣、管体爆裂、节箍泄漏。综合考虑各项载荷的影响,评价管柱安全性时应计算管体的三轴应力,并取合理的安全系数作为评价管柱安全性的依据。采用该方法,计算工作量少,针对性强。管体三轴应力的计算式为:
(7)
式中:σtri为管柱三轴应力,MPa。
套管柱接箍的三轴应力有相似的计算公式[10],在相关标准中有详细描述,本文不再赘述。
2 压裂时井口最高安全限压的确定
压裂作业时,泵压为现场重要的限定参数。保证管柱安全性的重要手段就是控制最高安全限压。一般的做法是假设一种较为极端的井况,据此井况设定最高泵压。
极端的压裂作业工况设定为:在压裂过程中遭遇砂堵,压裂排量降为0。此时泵压ppump=Δpi,油套环空压力 Δpo=0。根据这一条件,利用式(7)计算管柱的三轴应力,并根据管柱材料的许用应力,计算管柱的安全系数。
油层套管外的压力是这样设定的。不考虑水泥环、裸眼段地层压力和钻井液密度影响,假定油层套管外为清水。对于压裂作业来讲,在这样的假设条件下,管柱的安全性计算结果是偏安全和保守的。
根据API RT 5C3的推荐,取三轴应力安全系数值1.25作为计算参考标准,确定理论泵压的极限值。计算式为:
(8)
式中:K为计算安全系数;[σ]为管柱材料的许用应力,MPa;
3 计算结果的验正与准确性分析
采用上述方法,在三轴应力安全系数等于1.25时得到的泵压值作为理论极限泵压。对新疆油田公司5口压裂事故井进行事后安全性校核计算,理论极限泵压和油层套管实际破坏泵压值如表1所示。
由表1可以看出, 1#井为直井,按本文所述的计算方法求得的理论极限泵压略小于油层套管破坏泵压,误差为-6.25%,计算准确度较高,且具有合适的安全余量,对于压裂施工作业具有指导意义。对于水平井,按本文所述的计算方法计算出的理论极限泵压均大于油层套管破坏泵压值,误差数值随着水平段长度增加而变大。油层套管在低于理论极限泵时发生失效,这对于压裂作业来讲是危险的,理论计算值失去了指导意义。
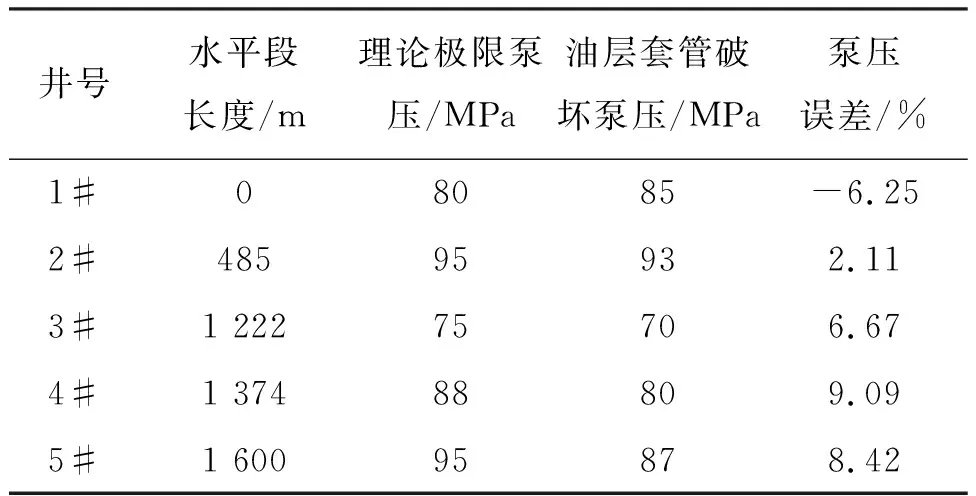
表1 事故井理论极限泵压与油层套管破坏泵压对比
对于水平井,现有的管柱安全性计算方法没有考虑油层套管在下入过程中的损伤对管材强度的降低,这使得计算获得的理论极限泵压值全部高于实际的套管破坏泵压值。根据表1的数据绘制图1,得到泵压误差值与水平段长度的关系曲线。

图1 水平段长度与极限泵压计算误差关系
由图1知,泵压误差数值与水平段长度呈近似正比关系,可以用一个简单的拟合公式来描述泵压误差值y与水平段长度x的函数关系。根据现有的统计数据,该拟合公式为y=0.009 1x-4.539 2,拟合优度为0.927 2。油层套管下入时,对管柱强度影响较大的因素较多[11-16],例如水平段长度,轨迹是否合理、裸眼井壁光滑程度、泥浆降阻性能优劣等。难以用一个科学的公式来准确描述这些因素对套管强度的影响。本文仅分析了水平段长度与泵压计算误差之间的关系,初步探索了降低这种计算误差的方法。
4 计算方法在水平井中的应用
在水平井中,管柱安全性计算应考虑管柱在下入过程中受到的损伤对其强度的影响,让适用于直井管柱安全性的计算方法在水平井上具有实际指导意义。关键是根据水平段长度适当提高三轴应力安全系数值,得到一个略小于实际套管破坏泵压的理论极限泵压。
以1#直井中二者的误差值-6.25%为基准,将上述泵压误差拟合公式计算出的与水平段长度相应的泵压误差值提高到该基准值。然后以相同的幅度提高三轴应力安全系数。以修正后的三轴应力安全系数为依据,计算新的理论极根泵压。如表2所示。

表2 采用修正后的安全系数计算的理论极限泵压与实际破坏泵压对比
由表2可以看出,使用修正后的三轴应力安全系数计算出的理论极限泵压与实际油层套管破坏泵压值的差值已经小于5 MPa。但是,仍有理论极限泵压高于套管破坏泵压的现象。例如5#井,新的理论极限泵压比实际油层套管破坏泵压高1 MPa。因此,以新的理论极限泵压值指导压裂施工作业,还应该留出一些安全余量,例如降低5 MPa压力,这样更能保证施工作业的安全限压是安全的、合理的。
该方法简单、易操作,计算结果的准确性较高。依据此值可以取一个较小的施工余量,在确保管柱安全性的同时,最大程度方便现场施工作业,具有较好的指导意义。
5 结论
1) 采用基于静态受力分析的方法计算压裂作业过程中油层套管的安全性,对于直井来讲,有较高准确性,可以直接用于指导直井套管压裂作业。该方法用来计算水平井的油层套管安全性时,结果不准确,需要适当提高相关安全系数。
2) 对于水平井,采用该方法计算油层套管的安全性时,在水平段长度为1 600 m时,三轴应力安全系数应当提高16.27%。安全系数提高幅度与水平段长度呈近似正比。
3) 由于事故井统计数据较少,在更长水平段的情况下,理论泵压极限值与油层套管实际破坏泵压之间的误差是否仍然满足近似正比关系,尚不能肯定,需要更多现场数据的支持。

