汽车电子节气门自适应模糊滑模控制器

任继愈，童 亮，党瑾希，许永红

（1.北京信息科技大学 机电工程学院，北京 100192；2.北京工业大学 环境与能源工程学院，北京 100124）

汽车电子节气门作为电控燃油喷射系统关键组成部件之一，通过直流电机和角度传感器来实现电子控制，避免了机械直连式节气门开度仅由加速踏板位置决定的缺点，同时保留了机械式节气门优良的响应特性，被广泛应用于发动机进气量控制[1]。汽车电控单元根据车辆运行状态和加速踏板信号计算出节气门最佳开度，将对应的电压信号送到驱动电路模块，驱动直流电机使节气门达到最佳开度位置，从而使发动机达到最佳空燃比。因此，节气门开度控制的动态响应速度和精确度直接影响着发动机的动力性能和燃油经济性。

电子节气门控制系统中存在着库仑摩擦、粘性摩擦及复位弹簧和齿轮间隙等非线性因素，在工作过程中还会遇到气流冲击扰动、节气门阀片产生油污积碳、齿轮磨损和节气门参数变化等问题，这些使得节气门开度的精确控制变得愈加困难[2]。国内外研究人员针对这些问题提出诸多控制策略：Deur 等[3]在PID 控制器的基础上加入前馈控制器、摩擦和跛行回家效应的非线性补偿器，并利用自适应模型对以上控制器参数在线调整，实现了节气门开度的精确控制[3]。Gritli 等[4]采用Takagi-Sugeno 模糊推理模型来逼近电子节气门非线性系统模型，并基于并行分布补偿的方法设计了非线性输入观测器，用于估计节气门阀片位置，形成状态反馈控制律，该方法能很好地抑制扰动和快速的瞬态响应。Montanaro 等[5]提出了一种离散时间模型参考自适应控制方法，并在发动机上进行了电子节气门性能测试实验，结果表明该方法对系统非线性具有较强的鲁棒性。徐金榜等[6]针对电子节气门数学模型难以精确建立、参数难以获取及非线性特性强，设计了内模控制器，能有效地提高系统响应速度，具有良好的鲁棒性。张邦基等[7]提出一种位置离散最优预见控制算法，降低了模型参数不确定性和对外界干扰的敏感度，提高了控制系统的稳定性和鲁棒性。孟志强等[8]针对电子节气门强非线性时滞及外部扰动不确定性的特点，设计了一种非奇异快速终端滑模控制器，提高了节气门开度控制的响应速度，具有较强的鲁棒性。

为了提高电子节气门开度控制的响应速度和精确度，本文设计了一种自适应模糊滑模控制器。建立了电子节气门非线性数学模型，采用积分滑模面设计切换函数作为模糊控制器的输入，利用模糊系统的万能逼近理论实现对理想控制律的逼近，采用切换控制律来补偿理想控制律与模糊系统的差值，并基于Lyapunov 方法设计自适应律对以上控制器参数进行实时调节。仿真和实验均表明所设计的控制器能实现节气门开度的精确控制，具有良好的动态性能。

1 电子节气门数学模型

电子节气门主要由直流电机、复位弹簧、减速齿轮组、位置传感器、节气门阀片等构成，图1 为电子节气门控制系统结构简图。

根据Kirchhoff 定律可得到电机电枢回路的电压平衡方程：

图1 电子节气门控制系统结构简图

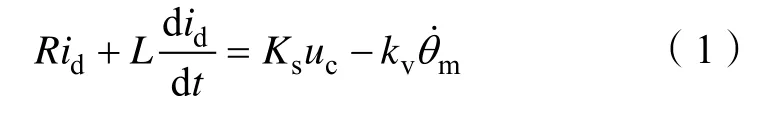
电机电磁转矩表示为

式中，R、L 和di 分别为电枢回路总电阻、总电感和电机电流，Ks为斩波器增益，kv为电机反电动常数；uc为控制输入电压，θm为电机旋转角，Cm为电机扭矩常数。

考虑到电机电感L 很小，且系统在运行中时间常数 Ta=L/ R比采样时间T 小，可忽略电机电枢电流动态特性影响[9]，令 L=0，则式（1）简化为

电子节气门系统存在的摩擦力矩主要由库仑摩擦力矩和粘性摩擦力矩构成[10]。摩擦力矩 Tf()可表示为

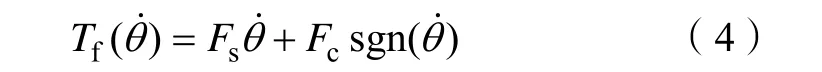
式中，sF 为粘性摩擦系数，cF 为库仑摩擦系数，θ 为节气门体阀片旋转角度。

为实现车辆“跛行回家”工作模式，复位弹簧由两个刚度系数相同的弹簧组成，可在直流电机不工作情况下使节气门阀片保持在一个小角度位置即静态位置，以允许一定量的空气进入气缸。在电子节气门运行时，无论阀片处于静态位置上方还是下方，均受到弹簧的复位力矩和预紧力矩的作用[11]。复位弹簧扭矩Tsp(θ) 可表示为

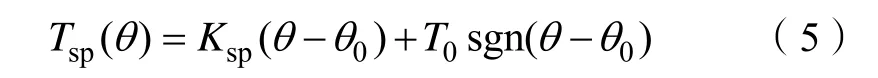
式中，0T 为复位弹簧预紧力矩，Ksp为复位弹簧弹性系数，0θ 为节气门静态开度。

根据扭矩守恒原理，以电机轴为参考的电机旋转角的动力学方程为

式中，Jm为电机轴转动惯量，km为电机轴阻尼系数，TL为电机负载扭矩。

以节气门体阀片轴为参考的阀片旋转角度θ 的动力学方程为

式中，Jt为节气门体阀片轴的转动惯量；gT 为作用在阀片轴上的扭矩；aT 为进气气流冲击阀片产生的阻力矩，考虑为未知扰动。

假定减速齿轮组的理想传动比为N，则满足以下关系：

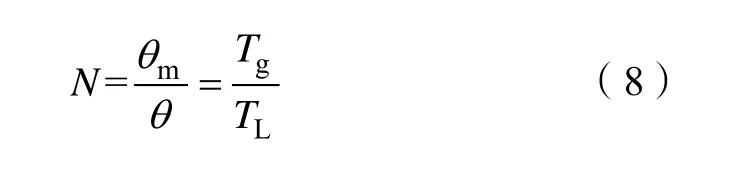
将式（2）、（3）和（8）代入式（6）得

将式（4）、（5）和（9）代入式（7）得

式（10）所建立的模型未考虑电子节气门齿轮间隙的非线性影响，以及工作温度变化所带来的参数变化的影响等，现将未考虑的非线性影响和未知扰动等一起作为总的不确定性叠加到系统中，记为有界扰动d。

定义状态变量：1x =θ，x2=，控制输入u =uc，则式（10）可表示为

式中：

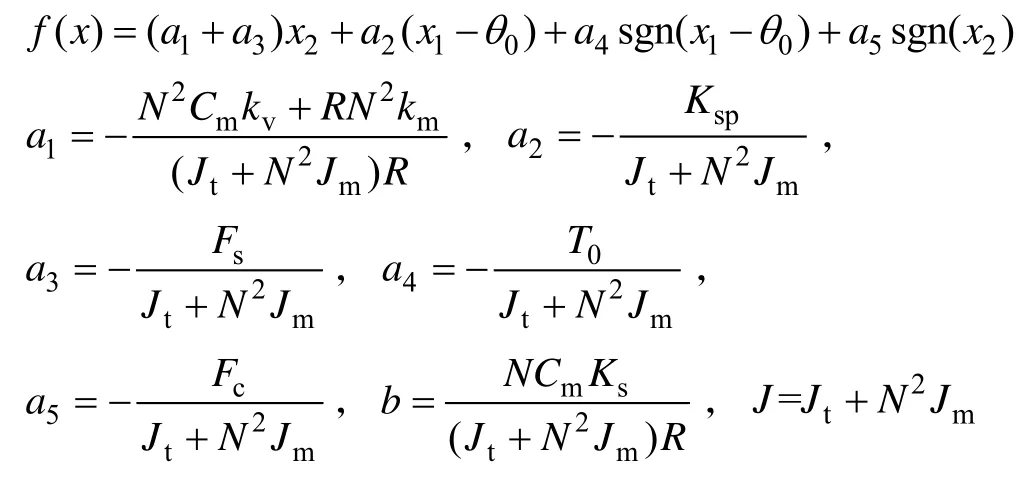
2 电子节气门控制器设计

电子节气门系统存在多种非线性因素且内部参数容易发生变化，易受外部干扰。为了实现节气门开度的精确控制和快速响应，提高系统的鲁棒性，本文将滑模控制结合模糊逼近用于电子节气门非线性系统，利用万能逼近定理和模糊语言实现对节气门模型未知部分的自适应逼近。基于Lyapunov 方法导出模糊自适应律，通过调节自适应权重来保证整个电子节气门闭环控制系统的稳定性和收敛性。图 2 为自适应模糊滑模控制系统结构框图。

图2 自适应模糊滑模控制系统结构框图

2.1 模糊滑模控制器设计

将式（11）转化为如下SISO 非线性系统：

取dθ 为节气门体阀片期望开度，定义控制系统误差为

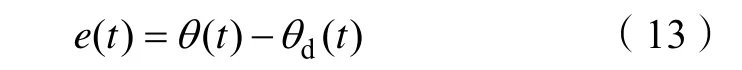
定义积分滑模面为

式中，1c、2c 为正常数。

对式（14）求导得

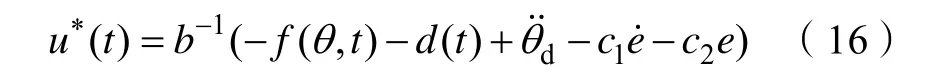
在实际控制中，电子节气门模型的部分参数会在运行中发生变化，采用由原有理论推导出的 f(θ,t) 和d(t)求得的 u*(t)难以对节气门阀片实现精确的开度控制。可利用模糊系统的万能逼近特性实现对理想控制输入 u*( t) 的精确逼近[12]。选择切换函数 s(t) 作为模糊系统的输入，构成一个单输入的模糊控制器。取iδ为可调参数，γ 为模糊基向量，则模糊控制器的输出为

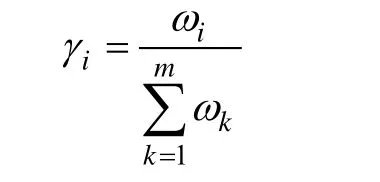
由于模糊系统具有万能逼近特性，则会有一个最优的模糊控制器输出 uf( s,δ*)去逼近 u*(t)。

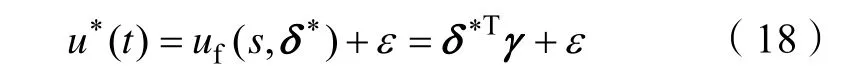
式中，ε 为逼近误差，满足| ε |＜ D。

采用模糊系统 uf逼近 u*( t)，有

采用切换控制 uq来补偿u*和 uf之间的误差，得到电子节气门总的控制律：

2.2 自适应控制算法设计

将式（15）代入式（16）得

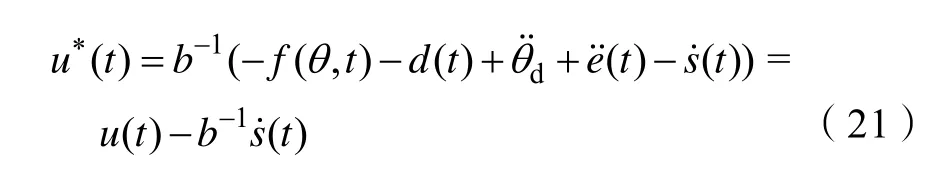
由式（18）得

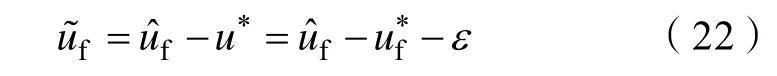
由式（20）和（21）得

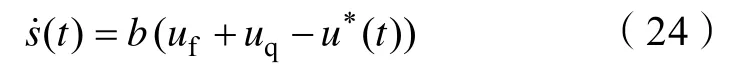
定义Lyapunov 函数为

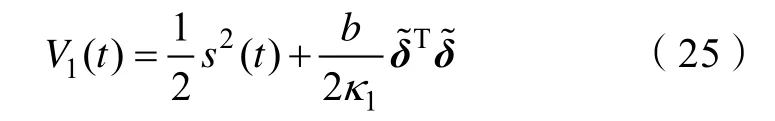
式中，1κ 为正实数。对式（25）求导并将式（23）和（24）代入得

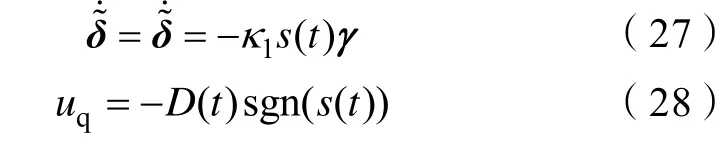
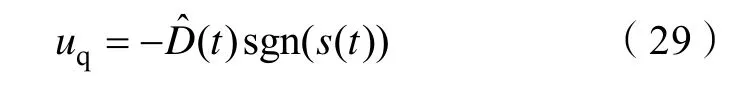
定义估计误差为

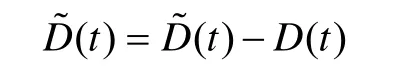
定义Lyapunov 函数为

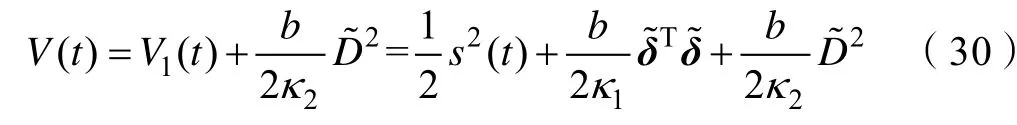
式中，2κ 为正实数。对式（30）求导得

则

为提高切换控制性能，采用具有光滑连续特性的双曲正切函数 h(s) 代替式（29）中符号函数sgn( s)，其表达式为

2.3 非线性扩张状态观测器设计

电子节气门自适应模糊滑模控制器设计中需要用到节气门阀片的角速度信号，而在实车应用中，电子节气门仅通过角度传感器提供两路互为冗余设计的阀片角度信号θ，角速度无法直接测量得到。扩张状态观测器可利用被控对象的输入输出信息对信号的n阶导数进行观测，其采用的高增益误差反馈使得观测器的动态远高于系统动态，可保证观测误差的快速收敛和足够高的估计精度[13]。非线性扩张状态观测器设计如下：

3 仿真与实验分析

3.1 Simulink 仿真结果分析

为了验证所设计的自适应模糊滑模控制器应用在电子节气门上的可行性，在Matlab/Simulink 环境下进行了仿真，将传统PID 控制和自适应模糊滑模控制对电子节气门的控制效果进行比较。其中针对积分滑模面采用以下5 种隶属度函数进行模糊化。

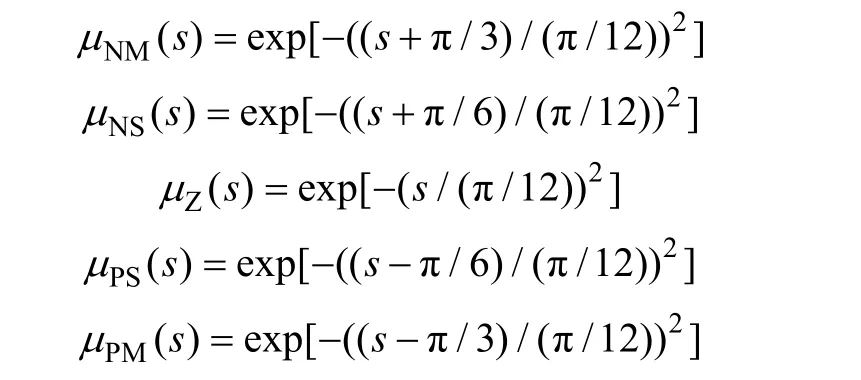
电子节气门系统模型参数值如表1 所示[14]，控制器及扩张状态观测器参数如表2 所示。节气门系统所受到的外部扰动为 d=6sin(π t)。节气门阀片初始状态为 x0=[0.0349 0]，节气门期望开度为频率0.4 Hz 的正弦信号，幅值变化范围为15～16°。传统PID 控制和本文所采用的自适应模糊滑模控制对电子节气门的控制仿真结果如图3—5 所示。

表1 电子节气门模型参数值

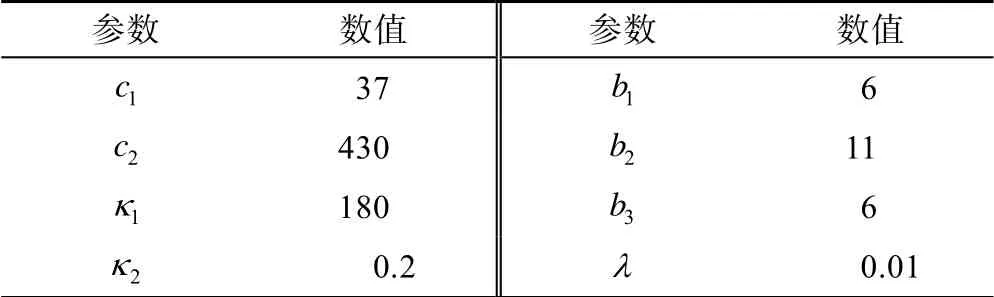
表2 控制器及观测器参数取值

图3 正弦信号跟踪响应

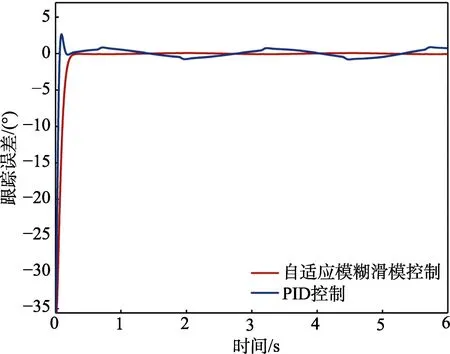
图4 正弦信号跟踪误差

由图3 可知，自适应模糊滑模控制能够实现节气门开度无超调跟踪，而传统PID 控制则出现一定的超调和响应滞后。由图4 可知，自适应模糊滑模控制对正弦信号的跟踪误差在稳态时在-0.1～0.1°范围内波动，而PID 控制的跟踪误差幅度明显大于前者，表明自适应模糊滑模控制具有更加优越的跟踪性能。

图5 为利用扩张状态观测器对节气门阀片角速度估计的变化曲线，在0.24 s 之后，估计值与实际值之差在-0.04～0.04 rad/s 范围内，表明观测器能够实现对阀片角速度的精确估计，且观测误差收敛快速，使自适应模糊滑模控制器只需要阀片旋转角度反馈就能实现对节气门系统的有效控制。

图5 节气门阀片角速度估计

3.2 电子节气门控制实验验证

为验证控制器的实际性能，现以BOSCH 公司生产的某一型号电子节气门为被控对象，利用dSPACE实时仿真系统搭建了电子节气门闭环控制快速原型实验环境，如图6 所示。RapidPro System 中的PS-FBD 2/1(DS1661)模块是基于Infineon TLE 6209 芯片扩展的全桥功率级模块，用于驱动电子节气门的直流电机。MicroAutoBox II 1401/1511/1514 作为dSPACE 实时仿真设备，用于采集节气门反馈的阀片角度信号，运行控制算法并输出PWM 波给RapidPro System。利用ControDesk 软件对控制参数进行在线实时调整，并采集实验数据。

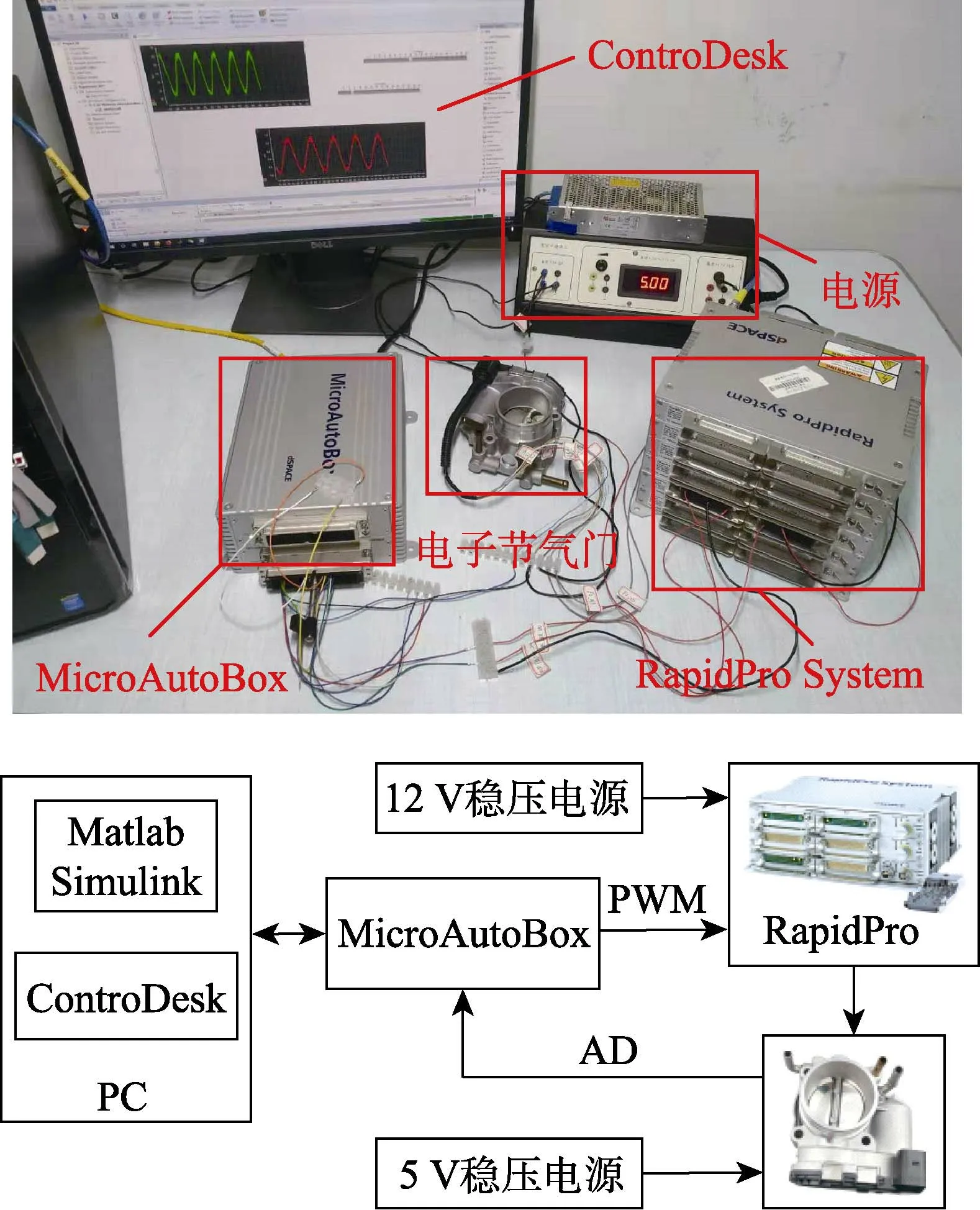
图6 电子节气门快速控制原型实验环境

电子节气门期望开度选用频率为0.4 Hz 的正弦信号来模拟汽车正常加减速运行过程，自适应模糊滑模控制和PID 控制对电子节气门的正弦跟踪响应结果如图7 所示。可以看出PID 控制存在一定量的跟踪迟滞和超调，且静差较大，这是因为节气门阀片转动方向发生变化时，非线性因素发生突变，且PID 控制参数固定，无法有效应对这种突变。而自适应模糊滑模控制对正弦信号响应快速，且无明显抖振现象，节气门阀片位置跟踪精度高、静差小，表现出良好的动态性能。

如图8 所示，采用变幅值的阶跃信号作为节气门期望开度来模拟汽车突然加速和减速时的运行过程，节气门开度幅值按15°→40°→20°→70°→50°→15°循环变化。可以看出，与PID 控制相比，自适应模糊滑模控制对不同幅值的阶跃响应均未出现超调，无论在大幅值阶跃还是小幅值阶跃响应时对节气门开度均跟踪精确，且具有较快的响应速度。

图7 正弦信号跟踪响应实验结果

图8 阶跃信号跟踪响应实验结果

4 结语

本文以汽车电子节气门为研究对象，建立了电子节气门非线性数学模型，将积分滑模控制结合模糊系统的万能逼近应用在电子节气门非线性系统上，并基于Lyapunov 方法导出模糊自适应律，通过调节自适应权重来保证整个电子节气门闭环控制系统的稳定性和收敛性。利用扩张状态观测器实现了节气门阀片角速度的准确估计。仿真与实验结果均表明，与传统PID控制相比，所设计的自适应模糊滑模控制对节气门期望开度跟踪精度高，无超调，并有效削弱了抖振现象，能满足电子节气门的控制要求。