隐零点问题中化隐为显的几种策略

魏东升

(江西省瑞金第一中学，342500)

在利用导数解题时,导函数零点的处理往往是一个关键环节,其中无法精确求解的“隐零点”成为学生解题的难点.对于这类问题,常见的处理方式主要有虚设零点和化隐为显两大类.其中化隐为显是指为了避免出现直接求导带来的隐零点问题,通过采取重新构造函数的方式,把隐零点转化为显零点的一种处理技巧.本文结合近几年的几道高考导数压轴题,探讨隐零点问题中化隐为显的几种主要策略,以供大家参考.

一、“双雄”构造

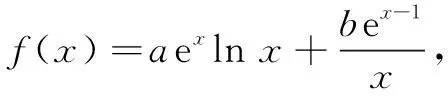
(1)求a,b;

(2)证明：f(x)>1.

解(1)a=1,b=2.(过程略)

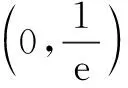
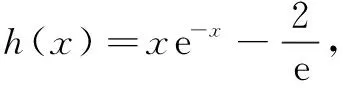
综上，当x>0时，g(x)>h(x),即f(x)>1.

评注本题对f(x)利用导数整体研究时会碰到隐零点问题,上述解法把证f(x)>1等价拆分成两个易求零点的函数(称之为“双雄”构造),回避了难点,简化了问题处理.

二、分离构造

例2(2017年全国高考题)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0.

(1)求a;

(2)略.

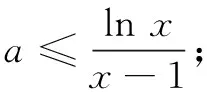
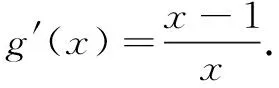
综上,所求a=1.

评注分离是处理函数或不等式问题的一种常见手段,通常用于分离参数,或者分离含有类似xlnx这样的超越式.本题中除了分离参数,还由f(x)含有xlnx而导致求导后出现隐零点问题,故而采取了将x和lnx分离的处理方式.

三、合并构造

例3(2018年全国高考题)已知函数f(x)=ex-ax2.

(1)若a=1,证明:当x≥0时,f(x)≥1;

(2)略.

解(1)当a=1时,f(x)≥1等价于(x2+1)e-x-1≤0.

设g(x)=(x2+1)e-x-1,则g′(x)=-(x2-2x+1)e-x≤0,g(x)在(0,+∞)单调减,可知当x≥0时,g(x)≤g(0)=0,即f(x)≥1.

评注对于含有ex的函数,根据求导法则,由于[f(x)ex]′=[f′(x)+f(x)]ex,所以像例3这样把f(x)≥1等价于(x2+1)e-x-1≤0,即将x2+1和e-x合并在一起求导,可以很好地避免隐零点的出现.

四、放缩构造

例4(2018年全国高考题)已知函数f(x)=aex-lnx-1.

(1)略;

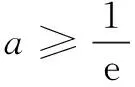
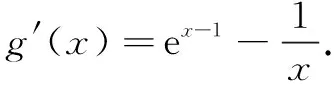
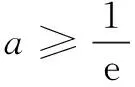
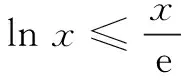
五、主元构造

(1)略;

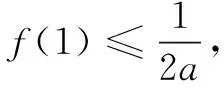
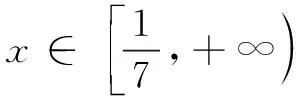
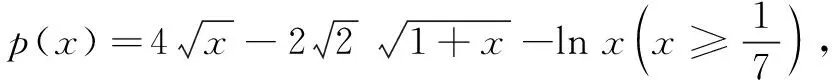
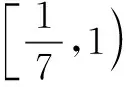
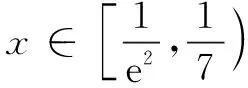
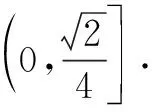
评注前四种构造策略都是建立在以x为主元的框架内进行的，对于含参的函数(比如例5)，可构造以参数为主元的函数来实现化隐为显的目的.

在导数压轴题的教学过程中,像这样以专题的形式介绍隐零点问题的处理策略,尽量一次性彻底地解决与其有关的问题,对学生解题水平的提升、逻辑思维的训练和核心素养的培养,想必都是极好的.