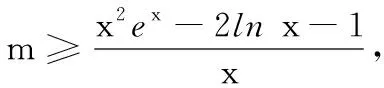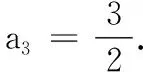高三数学综合测试

一、填空题(本大题共14小题,每小题5分,计70分)

1.已知集合A={-1,0,a2},B={-1,1},若A∩B=B,则实数a的值是______.

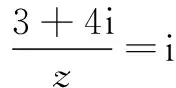
3.某校在高一、高二、高三三个年级中招募志愿者50人,现用分层抽样的方法分配三个年级的志愿者人数,已知高一、高二、高三年级的学生人数之比为4∶3∶3,则应从高三年级抽取______名志愿者.

4.一个算法的伪代码如图所示,执行此算法,最后输出的S的值为______.

S←0

I←1

WhileI<4

S←S+5

I←I+1

End While

PrintS

6.某校机器人兴趣小组有男生3名,女生2名,现从中随机选出3名参加一个机器人大赛,则选出的人员中恰好有一名女生的概率为______.

7.已知数列{an}是等比数列,Tn是其前n项之积,若a5a6=a7,则T7的值是______.

8.已知f(x)=cosx+e|x|,则f(3-x)-f(3x+1)>0的解集为______.

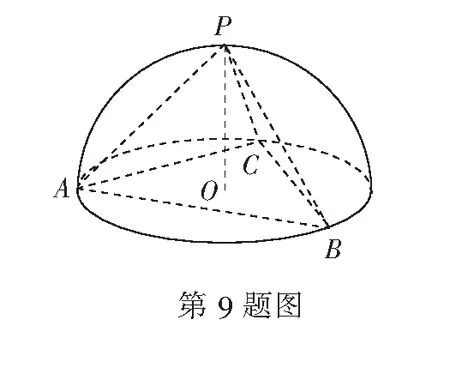
9.如图,已知正三角形ABC是一个半球的大圆O的内接三角形,点P在球面上,且OP⊥面ABC,则三棱锥P-ABC与半球的体积比为______.

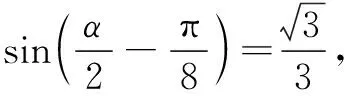
11.设[t]表示不超过实数t的最大整数(如[-1.3]=-2,[2.6]=2),则函数f(x)=|2x-1|-[x]的零点个数为______.

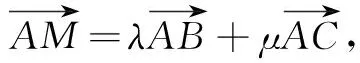
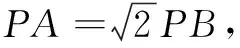
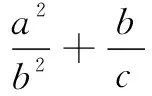
二、解答题(本大题共6小题,计90分)

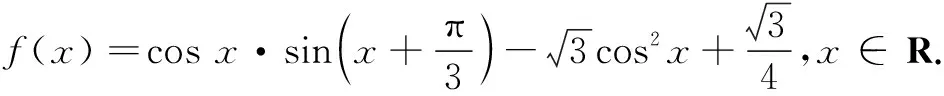
(1) 求f(x)的最小正周期和对称中心;

16.(本小题满分14分)如图,四面体ABCD被一平面所截,截面与四条棱AB，AC，CD，BD分别相交于E，F，G，H四点,且截面EFGH是一个平行四边形,AD⊥平面BCD，BC⊥CD.求证：

(1)EF∥BC；

(2)EF⊥平面ACD.

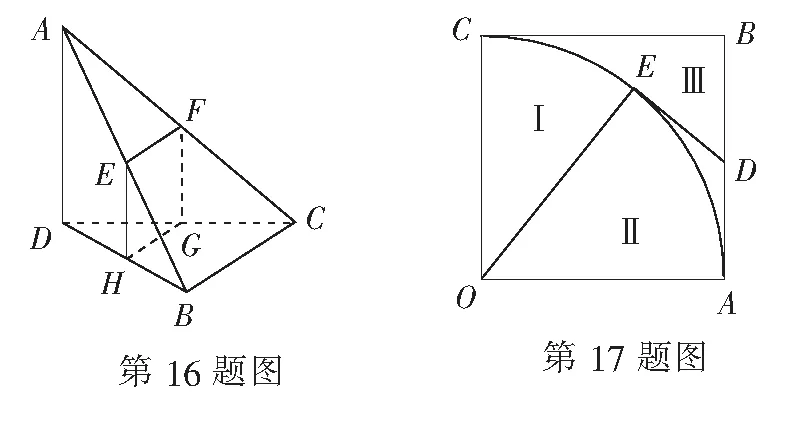
17.(本小题满分14分)如图,边长为1的正方形区域OABC内有以OA为半径的圆弧AEC. 现决定从AB边上一点D引一条线段DE与圆弧AEC相切于点E,从而将正方形区域OABC分成三块:扇形COE为区域I,四边形OADE为区域II,剩下的CBDE为区域III.区域I内栽树,区域II内种花,区域III内植草.每单位平方的树、花、草所需费用分别为5a、4a、a,总造价是W,设 ∠AOE=2θ.

(1) 分别用θ表示区域I，II，III的面积;

(2) 将总造价W表示为θ的函数,并写出定义域;

(3) 求θ为何值时,总造价W取最小值?

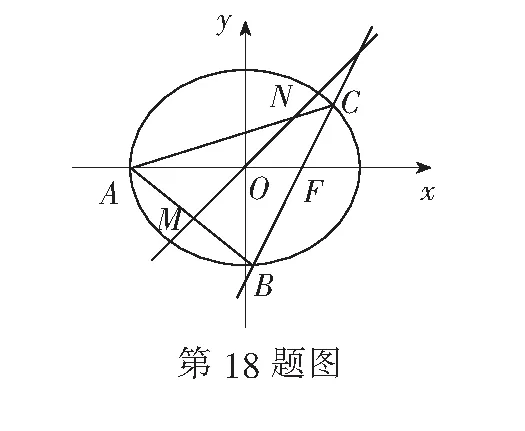
(1) 求椭圆E的标准方程;

(2) 若过O的直线m:y=kx与直线AB,AC分别相交于M,N两点,且OM=ON,求k的值.

19.(本小题满分16分)已知函数f(x)=ex-ax2(a∈R).

(1) 若曲线f(x)与直线l:y=(e-2)x+b(b∈R)在x=1处相切.

(i) 求a+b的值;

(ii) 求证:当x≥0时,f(x)≥(e-2)x+b;

(2) 当a=0且x∈(0,+∞)时,关于x的不等式x2f(x)≤mx+2lnx+1有解,求实数m的取值范围.

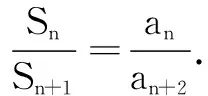
(1) 若S3=3,求a3的值;

(2) 若a2021=2021a1,求证:数列{an}是等差数列;

参考答案

一、填空题

1.±1;2.5;3.15;4.15;

二、解答题

16.(1) 因为四边形EFGH为平行四边形,所以EF∥HG.

又EF⊄平面BCD,HG⊂平面BCD,所以EF∥平面BCD.

又EF⊂平面ABC,平面ABC∩平面BCD=BC,所以EF∥BC.

(2) 因为AD⊥平面BCD,BC⊂平面BCD,所以AD⊥BC.

由(1)知EF∥BC,所以EF⊥AD.因为BC⊥CD,所以EF⊥CD.

又AD∩CD=D,AD、CD⊂平面ACD, 所以EF⊥平面ACD.

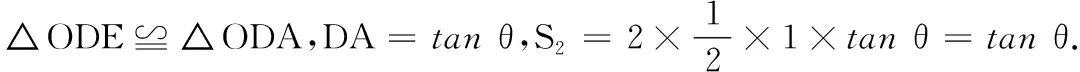
(2)W=5aS1+4aS2+aS3=a(3tanθ-4θ+π+1).

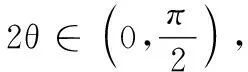
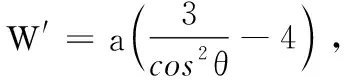
18.(1) 设椭圆E的焦距为2c,则直线l的方程为y=2(x-c),即2x-y-2c=0.

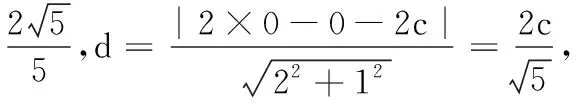
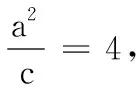
(2) 由(1)知l:y=2(x-1),设B(x1,y1),C(x2,y2).

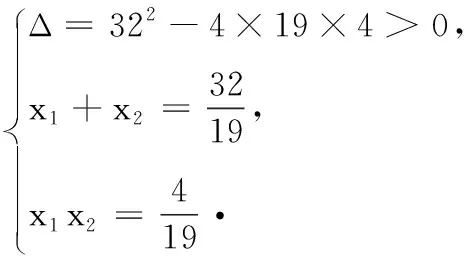
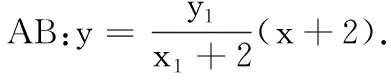
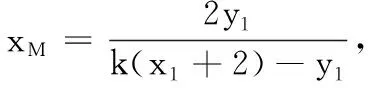
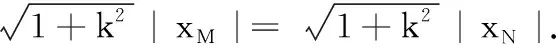
19.(1) (i)f′(x)=ex-2ax，令f′(1)=e-2a=e-2,得a=1.

所以f(x)=ex-x2,f(1)=e-1.

又切点(1,e-1)在直线l上,得e-1=e-2+b,b=1,所以a+b=2.

(ii) 由(i)知a=1,b=1,可设h(x)=ex-x2-(e-2)x-1(x≥0),则g(x)=h′(x)=ex-2x-(e-2),g′(x)=ex-2.

当xln 2时,g′(x)>0.所以h′(x)在(0,ln 2)单调减,在(ln 2,+∞)单调增.

由h′(0)=3-e>0,h′(1)=0,0

由此可知，当x∈(0,x0)∪(1,+∞)时,h′(x)>0；当x∈(x0,1)时,h′(x)<0.所以h(x)在(0,x0)单调增,在(x0,1)单调减,在(1,+∞)单调增.

又h(0)=h(1)=0,所以h(x)≥0,即f(x)≥(e-2)x+1,当且仅当x=1时取等号.

故当x≥0时,f(x)≥(e-2)x+b.

(2)先证ex≥x+1.

构造函数p(x)=ex-x-1,则p′(x)=ex-1.当x∈(0,+∞)时,p′(x)>0,p(x)单调增；当x∈(-∞,0)时,p′(x)<0,p(x)单调减.所以p(x)≥p(0)=0,即ex≥x+1.

因为x2ex-2lnx-1=ex+ln x2-2lnx-1≥x+lnx2+1-2lnx-1=x(当x+lnx2=0时取等号),所以m≥1.

当n≥2时,a2Sn-1=an-1an,故a2Sn-a2Sn-1=anan+1-an-1an,即a2(Sn-Sn-1)=an(an+1-an-1),即a2an=an(an+1-an-1),从而an+1-an-1=a2,所以数列{a2n-1}是等差数列,其首项为a1,公差为a2.

由a2021=a1+1010a2=2021a1,得a2=2a1.

所以a2n-1=a1+(n-1)a2=(2n-1)a1,a2n=a2+(n-1)a2=2na1,即an=na1,所以an+1-an=a1,数列{an}是等差数列.

|2n-2m|≤λ|n2-m2|.

不妨设m>n,则2m>2n,m2>n2,有2m-2n≤λm2-λn2,即2m-λm2≤2n-λn2对任意正整数m,n(m>n)恒成立,则2n+1-λ(n+1)2≤2n-2λn-λ≤0对任意正整数n恒成立，设Cn=2n-n2,则Cn+1-Cn=2n+1-(n+1)2-2n+n2=2n-2n-1.

设Dn=2n-2n-1,则Dn+1-Dn=2n+1-2(n+1)-1-2n+2n+1=2n-2.

当n≥5时,Dn+1-Dn>0,所以Dn>D5>0,得Cn>C5>0,有2n>n2,进而2n-2λn-λ>n2-2λn-λ.