洞悉教材意图 融入史学文化——从高尔顿的视角看正态曲线的教学

王 响

(湖北省武汉二中广雅中学,430010)

《普通高中数学课程标准》(2017年版)(以下简称《标准》)指出:“数学教材为‘教’与‘学’活动提供学习主题、基本线索和具体内容,是实现数学课程目标、发展学生数学核心素养重要的教学资源．”[1]由此可见教材在课堂教学中扮演了重要角色,它是实施教学的重要资源．但面对教材,不少教师往往“一笔带过”或“弃之不用”,没有真正领会到教材的编写意图,未能创造性地使用教材,从而也难以达成《标准》中所要求的教学目标．本文以人教版高中数学选修2-3“正态分布”的教学为例,尝试挖掘教材意图,设计教学片断,沿着高尔顿的脚步看正态曲线的抽象过程．

一、背景分析,揣摩意图

正态分布最早是由棣莫弗(De Moivre)、斯特林(Stirling)等数学家在二项分布的极限分布中被发现,后经欧拉(Euler)、拉普拉斯(Lapalace)、勒让德(Legendre)和高斯(Gauss)等人在天文学和测地学的数据测量误差的研究中推广使用的.他们都对此做出了卓越贡献,特别是高斯基于误差正态分布的最小二乘理论对后世的影响极大,因此正态分布也被冠名高斯分布．正态分布不仅是属于概率的范畴,同时它也是统计的基石．在19世纪,比利时统计学家凯特勒对正态分布情有独钟，英国生物学家高尔顿受此影响，开始用统计的方法研究遗传进化问题,并设计了一个钉板装置把正态分布的性质用于解释遗传现象,成为正态分布发展的又一推动力量[2]．

教材中通过介绍高尔顿钉板实验,给出一个小球堆积图,然后从频率的角度画出一个频率分布直方图,最后增加试验次数得到正态曲线．通过简短的文字以及三幅图形来得到如此美丽的曲线,这引起了笔者的思考:一是编者为何通过这种方式引出正态曲线?其意图是什么?从学生的角度是否能够理解?二是与其他引入方式相比,教材有何优势?三是如何依托教材,在结合《标准》对教学资源要求充分利用的基础上，让本节课发挥出更大的育人价值？带着这些疑问,笔者对正态分布的产生与发展进行了深入分析,总结出以下两点意图:其一，让数学史文化融入数学课堂,感受数学文化的魅力.由于高斯等数学家发现正态分布的理论性较高,不易于学生接受,因此本节课从高尔顿钉板装置出发,通过试验的方式让学生了解古人奇妙且艰辛的探索之路．其二，沿着高尔顿的脚步重演正态曲线的形成过程,让学生经历从身高、体重等具体的数据到高尔顿钉板中直观的小球堆积图,再借助频率分布直方图,最后抽象出正态曲线的过程,使学生经历直观表象抽象的过程,对培养学生的数学抽象能力,提升数学抽象素养具有重要价值．

基于以上背景,笔者尝试以下三个教学片段的设计,旨在领略教材意图,融入史学文化,为核心素养的课堂教学做一点探讨．

二、教学片段及设计意图

片段1具体—直观

高尔顿的背景简介:十九世纪中叶,英国著名科学家——弗兰西斯·高尔顿,受其表兄达尔文的《物种起源》的影响,开始了对生物遗传进化问题的研究．研究中他发现了一些有趣的现象:比如某地区同一年龄人的身高、体重数据中,特别高或特别矮的人都比较少;特别轻或特别重的人也都较少!这样的分布规律背后,其决定因素究竟是什么呢?经过深入分析他发现：这些数据的分布与高斯等数学家研究的正态分布很吻合．为了更加深入研究这类问题,他设计了一个钉板装置(高尔顿钉板)来模拟正态分布,并将试验结果呈现得非常直观．

(高尔顿钉板介绍:在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙座位通道,前面挡有一块玻璃．让一个小球从钉板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,当小球碰到小木块时从左边落下与从右边落下的机会相等,碰到下一木块又是如此,最后落入底板中的某一球槽内．)

活动1高尔顿钉板试验

师：(提问)任意放入一个球,这个球落入哪一个球槽事先是否能够确定?

众生:不能确定!

师：(追问)小球与某个小木块碰撞后,会影响与下一个小木块的碰撞结果吗?

众生:不会,小球与每一个小木块碰撞后向左或向右落下的机会均等.

师:由此我们知道每一个小球在下落过程中与众多小木块发生碰撞,每次碰撞的结果不受上一次碰撞的影响,碰撞后小球向左或向右下落的机会均等,因此小球的堆积高度是众多随机碰撞的结果．

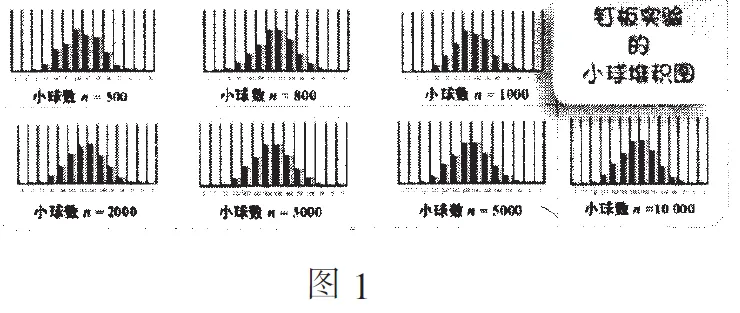
师:现在让我们聚焦在小球堆积图的形状上,观察当小球数量增加时,堆积图会呈现出什么样的特点呢(图1)?

(师生合作模拟钉板试验,并呈现出试验结果,如图．n=500,800,1 000,2 000,3 000,5 000,10 000.)

师:同学们发现了什么规律呢?

生1:这些球槽中都是中间球槽落入的小球多,两边球槽落入的小球少,左右基本对称．

师:对,和同学们前面猜想的一致,还有没有呢?

生2:随着小球数增加,后面四幅图基本一样的．

师:也就是说球槽中小球的堆积形状都呈现出中间高,两边低的特点,并且随着次数的增加,上述特征越发凸显和稳定．

设计意图不少教师都是从身高、体重或钢管内径的数据出发,画出频率分布直方图,最后得到正态曲线,但数据不随机因素众多且组数有限,是否对于每一组数据都有这样的情形,学生可能会产生疑惑,也无法反映出科学家们努力探索的过程．而通过高尔顿钉板试验就可以将身高体重的数据转化为小球落下时所对应的数据,将具体身高、体重等数据的分布抽象为直观形象的小球堆积图,既可以模拟多次的独立重复试验,又可以形象直观地表示出分布规律,让学生直观地感知小球堆积图“中间高两边低”的特点，也验证了学生试验前的猜想,使学生参与到课堂中来．

又根据概率的统计学定义:概率是频率的稳定值(对于钉板实验,如果随着试验次数的增加,小球落在某个球槽中的频率稳定在某个常数,那么这个常数就是小球落在该球槽概率的近似值),来启发引导学生还需将这个堆积形状规律转化为频率规律,才有可能求出相应的概率．

片段2直观—表象

师:球槽中小球的堆积高度反映了什么?

生3:频数分布规律.

师:如何利用所学的知识进一步研究小球的分布情况呢?大家通过小球的堆积图联想到了什么?

生4:频率分布直方图．

活动2画出频率分布直方图(图2)

(大部分学生都能通过列出频率分布表,然后以球槽编号为横坐标,以小球落入某个球槽中的频率/组距为相对应的纵坐标,画出频率分布直方图,个别学生无法下手．)

师:观察这个图,你有什么发现?

生5:与球槽中小球的堆积图形状类似,其频率分布直方图也是中间高两边低,左右基本对称,形状大小基本稳定．

设计意图通过层层设问来引导学生从小球堆积图联想到频率分布直方图,动手画出直方图的过程,能使学生对服从正态分布的变量特征有更深刻的体会,并且从中培养学生动手操作、数据分析的能力．

从直观的小球堆积图到更加准确、形象的频率分布直方图．中间高两边低、左右对称的正态曲线的特征已初露原形,使学生进一步加深了对正态分布特征的理解．但是在数学中仅有这样直观的表示还不够,理想的是能用数学式子表示这个规律,从而为正态曲线的抽象做下铺垫．

片段3表象—抽象

师:大家回顾一下必修3的内容,要想让样本的频率分布直方图更好地反映总体的分布规律,我们是怎么做的?

生6:使小球数逐渐增加,组距不断缩小．

活动3几何画板演示

师:通过计算机模拟试验,我们发现了什么?

生7:这个直方图的轮廓由一条折线逐渐变成了一条光滑的曲线．

师:进一步抽象．我们将这条曲线抽象出来,放在平面直角坐标系中,大家发现这条曲线具有什么样的特点呢(图3)?

生8:中间高,两边低,左右基本对称．

师:非常好!我们就把这样一条曲线叫做正态曲线,由于这条曲线的外形像一个倒扣着的钟,所以我们也称他为钟形曲线．

设计意图从旧知到新知,学生经历从频率分布直方图到正态曲线的抽象过程,更进一步从图象的角度直观地理解“形如钟形,中间高、两边低,左右对称”的特点,借助几何画板让学生直观形象地感受从离散型随机变量到连续型随机变量的过渡．

三、结束语

随着新课程标准的颁布,各类教材也在陆续编排出版.作为课程标准的载体,教师要善于利用教材,挖掘教材深意,充分发挥出教材中教学情境、例题与习题、数学活动的作用,理解其设置意图,读懂其中所蕴含的数学知识与能力、数学思想和方法,真正用好教材而不是教教材、照搬教材,更不是不要教材．同时也应该根据学生的特点,创造性地去使用教材,通过启发引导让学生学会自主学习,使学生核心素养的提升落实到每一节课堂中去．