非对称结构圆锥曲线问题的求解策略——以2020年高考全国Ι卷第20题为例

涂序星

(广东省佛山市乐从中学，528315)

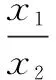
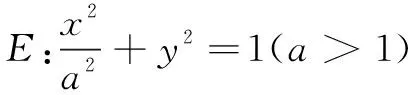
(1)求E的方程;

(2)证明:直线CD过定点.

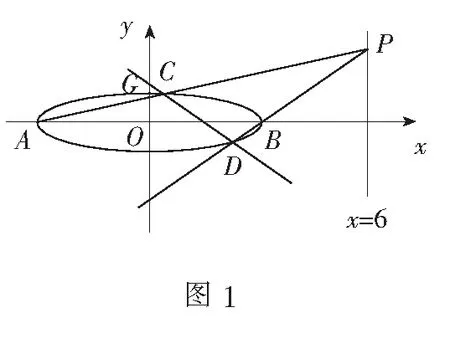
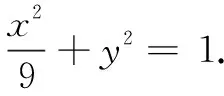
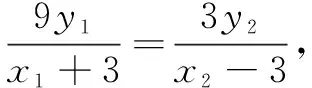
①

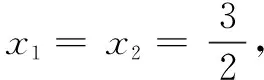
解题至此,我们发现①式是非对称结构,无法直接用韦达定理代入解决,高考时很多学生止步于此.笔者经过一番探究运算,总结出解决此类非对称结构圆锥曲线问题的几种思路,供读者参考.

思路1平方法

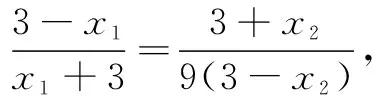
整理得 4x1x2-15(x1+x2)+36=0.

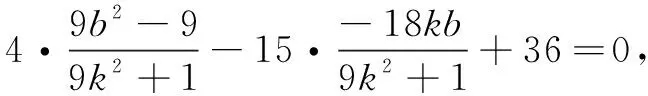
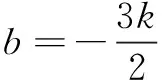
思路2用椭圆第三定义

②

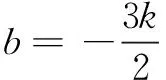
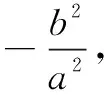
思路3积转为和

直线CD的斜率不可能为0,可设直线CD的方程为x=my+t,C(x1,y1),D(x2,y2).

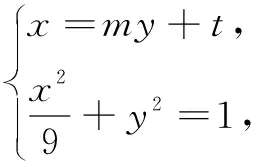
③

思路4设线解点

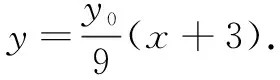
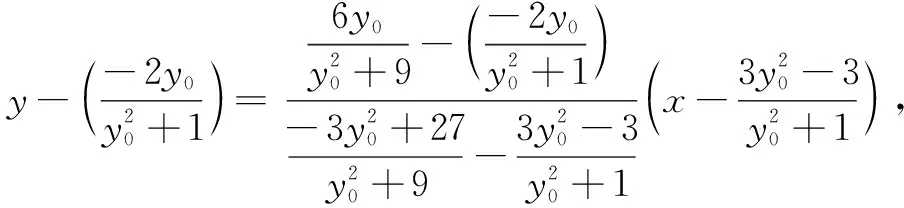
评注思路4为了回避出现非对称结构,不直接设直线CD的方程,而是先通过设直线AP方程求出点C的坐标,同理得出点D的坐标,从而得到直线CD的方程；再整理得出直线CD过定点.思路清晰顺畅,学生容易接受,但计算量偏大.

思路5平移坐标系+齐次化变换

x′2+9y′2-6x′=0.

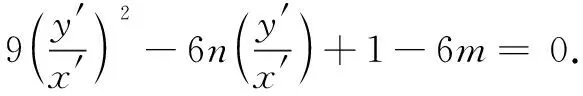
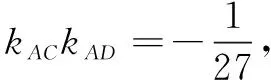
纵观以上解题思路,化归与转化这一重要思想的应用体现得淋漓尽致,大道至简.非对称结构圆锥曲线问题大部分有高等几何命题背景——极点极线知识,深受命题专家亲睐,在高考和各地模拟卷多次出现,如2010年江苏卷、2011年四川卷、2001年广东卷.