一道线性规划试题的多思路求解

孙道斌

(山东省菏泽市牡丹区教研室，274000)

“注重学科的内在联系,整合知识网络交汇”一直是高考命题“能力立意”的宗旨,而线性规划最值问题恰好是交融性极强的素材.下面,笔者就以2020年新课标全国Ⅲ卷理13题(文13题)为例,通过不同的解题方式对这种题型的解题策略尝试粗浅的探讨,希望对2021年的高考有所启示.

题目若实数x,y满足约束条件

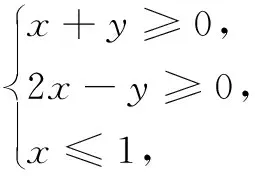
则z=3x+2y的最大值为______.

策略1平移目标函数,通法通用

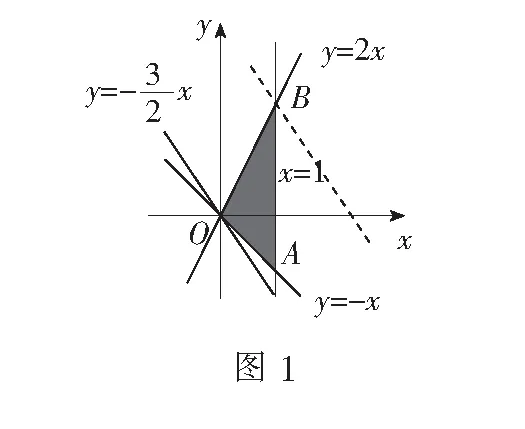
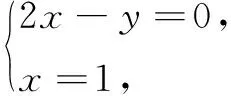
故zmax=3×1+2×2=7，填7.

评注先利用线性约束条件作出可行域,然后根据等值线的几何意义通过平移目标函数明确最大值点,再通过解方程组求得最大值点的坐标,得出目标函数的最大值.这种解题思路当属经典解法,能有效地培养学生数形结合的能力.

策略2替换变量,出奇制胜

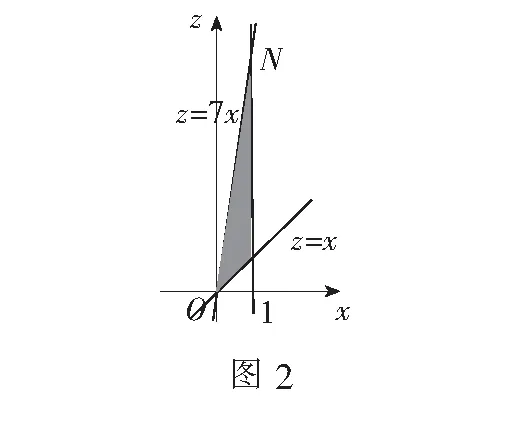
新不等式组所表示的区域如图2.由图2可知z的最大值为区域中最高点N的纵坐标.

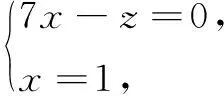
∴故zmax=7，填7.

评注变量替换,不但彰显了个性,而且有效避免了“平移”,从而使目标函数值的取值范围一目了然,极大地减少了出错的概率,同时也使问题的解答变得更为简捷、直观.

策略3构造向量,另辟蹊径

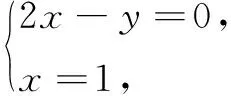
故zmax=3×1+2×2=7，填7.

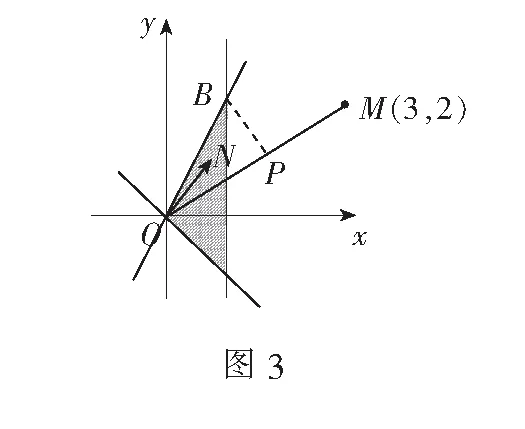
评注利用向量法求解线性规划的最值问题,不仅体现了向量的工具性,而且拓宽了数学解题的思维和方法，特别是对于求解系数a,b较复杂的目标函数时有明显的优势.

策略4应用不等式组,化繁为简

评注先从目标函数解出x或y,并将其代人约束条件,然后利用不等式的性质解不等式组,轻车熟路使得问题迅速获解.这种解法省去了作图,可以有效地节省解题时间,从而化繁为简，出奇制胜.

策略5几何问题代数化,数形结合

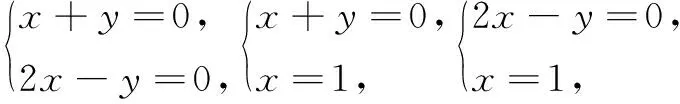
因为z=3x+2y存在最大值,且最大值只能在三个顶点处获得,比较可知zB>zA>zO,所以z=3x+2y的最大值为7.

评注由教材可知，当点P(x,y)落在可行域上的某个顶点或某条边界所在线段时,线性目标函数z=ax+by取得最值(反之也成立).由此,通过几何问题代数化,可用解二元一次方程组、求函数值的方法代替线性规划中作图法求解,提高解题效率,使得问题的解决变得更简单、便利.

对比以上五种策略下的解法，不难看出,线性规划是沟通几何知识与代数知识的重要桥梁,是数形结合的集中体现,解题的关键是理解目标函数的意义.同时,也可以看出,该问题与其他知识进行交叉融合,不仅体现了高中数学常用的数学思想,如数形结合思想、转化与化归思想、动态思想和建模思想,而且也体现了对学生综合分析问题的能力、逻辑思维能力以及解决实际问题的能力的要求.