用三点共线定理中λ的几何意义快速解题

陆琳琳

(浙江省东阳市第二高级中学,322100)

近几年的数学高考题十分强调几何背景和代数性质的结合,而平面向量具有代数与几何的双重特点,是联系高中各知识点的重要媒介.有一类以线段或直线为背景的向量题常与三点共线定理有关,利用共线定理中λ的几何意义,可帮助我们快速解题.

一、定理呈现

定理A,B,C三点共线,当且仅当对于平面内的任意一点O,存在实数λ使得

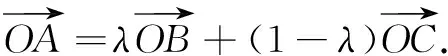
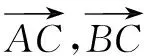
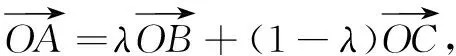
综上,得证.

从上面的证明过程中,我们可以发现共线定理中的λ的几何意义就是确定点A在直线BC上的位置.利用λ的几何意义,我们可以解决线段的比例问题,也可把向量模的最值问题转化为定点到动点、定直线或定曲线上的点的距离的最值问题.

二、应用举例

1.用λ的几何意义解决面积的比值问题

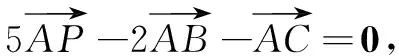
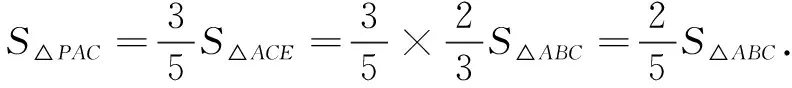
评注本题由λ的几何意义快速确定点E与P的位置,从而得到三角形面积的关系,解题速度明显优于其他方法.

2.用λ的几何意义求向量模的最值

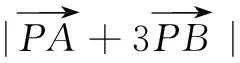
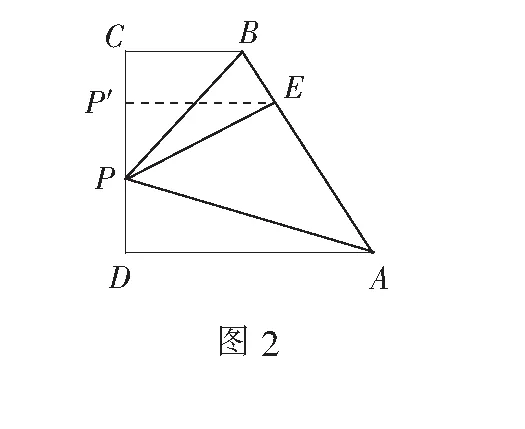
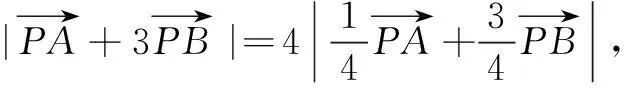
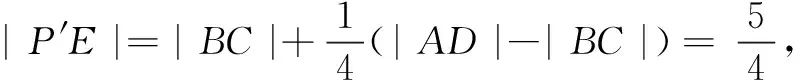
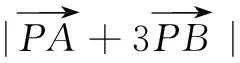
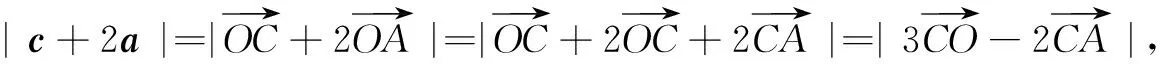
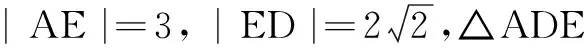
评注上述解答技巧1是由题设挖掘出点E在线段AD上这个隐含条件,技巧2同例2,由共线定理对|c+2a| 恒等变形,利用λ的几何意义确定点E的位置,将问题转化为定点E与动点的距离的取值范围.由共线定理确定点E的位置时,可依据向量加法的平行四边形法则或三角形法则，清晰确定点E在线段AD上或其延长线上.

例4已知a,b满足|a|=1,|2a+b|+|b|=4,求|a+b| 的取值范围.

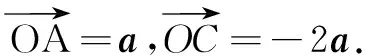
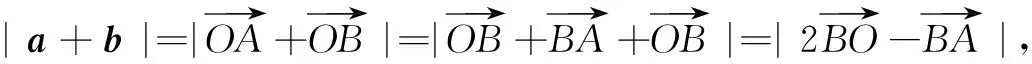
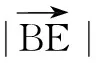
评注本题先运用动静结合得思想,探索出点B的轨迹为椭圆;再由共线定理将问题转化椭圆上的点到椭圆中心(定点)的距离的取值范围问题,由椭圆基础知识轻松获解.

综上,在平面向量问题中,当我们看到两个向量进行线性运算时,可找到共线三点,再准确利用共线定理中λ的几何意义,就能将问题转化为平面几何中的定点到动点的问题,利用平面几何的知识解决问题.

关于向量模的最值问题(如本文中后三个例子),也可以用解析法或向量模的三角不等式进行尝试求解,但解题过程都没有上述解答简便.读者不妨试一试.