基于黏聚力裂缝模型的反倾层状岩质边坡倾倒破坏模拟

马文著，徐 衍，李晓雷，陈 敏

(1.河北工业大学土木与交通学院，天津 300401；2.北京科技大学土木与资源工程学院，北京 100083; 3.中水北方勘测设计研究有限责任公司，天津 300202；4.宿迁市宿城区水利局，江苏 宿迁 223800)

反倾层状岩质边坡的倾倒破坏是常见的一种地质灾难，尤其是在坡脚开挖或河谷下切作用下，很容易发生倾倒失稳。如Wali滑坡等[1]，正是由于倾倒变形诱发的大规模滑坡。很多矿山工程和水利水电工程就面临这样的工程问题，如三峡库区龚家方滑坡[2]、湖北鹤峰红莲池铁矿山体崩塌[3]等。因此，研究此类边坡的倾倒破坏机制和影响因素对滑坡灾害的控制和治理具有非常重要的意义。

前人对岩质边坡的破坏问题进行了大量数值计算与模拟研究。在研究反倾层状岩质边坡的破坏机制时，能够考虑大变形的离散元程序(如UDEC)已经被不少学者用来进行层状岩质边坡的分析。刘云鹏等[4]采用UDEC软件，以都汶公路一处边坡为例，研究了其在地震响应下的变形破坏机制；黄波林等[5]对三峡库区廖家坪危岩体进行了离散元模拟分析；王章琼等[6]借助离散元方法以红莲矿山为背景，分析了多因素下坡体变形破坏特征；Gu等[7]对龚家方滑坡进行离散元模拟，概化出“悬臂梁模型”，用以解释坡体的破坏机理。Alzoubi等[8]采用UDEC损伤模型(UDEC-DM)对反倾层状岩质边坡进行离心破坏模拟，结果表明：岩层的抗拉强度是导致坡体发生倾倒破坏的关键因素。

在研究反倾层状岩质边坡倾倒破坏在连续小变形条件下的成因机理方面则主要采用有限元模型来进行计算。王宵等[9]以某梯级电站厂后边坡为例，构建三维有限元模型，深入阐明了“似层状”岩质边坡的具体演化过程；代仲海等[10]通过对反倾层状边坡的有限元分析，揭示了其破坏面发展的时空规律；王宇等[11]运用节理有限元法，构建出反倾层状岩质边坡有限元模型，探讨了此类坡体的变形破坏机制及稳定性影响因素。

基于F-DEM方法(有限元-离散元耦合)的连续-离散数值模型既能研究岩石弹性阶段的小变形机理又能够分析大变形情况下岩石的破坏模式。针对边坡变形破坏问题，陶志刚等[12]以戒台寺古滑体为背景建立连续-离散模型对其开裂破坏过程进行研究，判断出古滑体最危险区域。陈小婷等[13]以巫山县长江左岸危岩体为例，证明了将连续-离散模型用于边坡破坏研究的可行性。有限元黏聚力裂缝模型(Cohesive Crack Model, CCM)是连续-离散模型中的一种，该模型最早由Dugdale[14]和Barenblatt[15]提出，并在晶体、岩石等脆性材料裂纹扩展研究中得到广泛应用。相较于其他连续-离散模型，CCM更注重模拟物质的微观破裂形态。Jiang等[16]运用此方法进行了刀齿破岩的数值模拟研究，得出不同形状压头在侵入岩石时侵入力与侵入距离的关系。Jaime等[17]采用此方法进行了岩石切割的模拟研究，结果表明：此方法可以合理地模拟岩石切割过程。Wang等[18]将此方法与扩展有限元法进行耦合，分析了水力作用下岩石的裂隙扩展过程，得出岩石裂缝几何形状对裂纹扩展应力的影响。CCM在模拟岩石破坏行为方面应用广泛，但针对边坡破坏问题的算例极少。

本文在通用有限元软件ABAQUS平台上，通过全局嵌入零厚度黏聚力单元，建立反倾层状岩质边坡CCM。经过参数标定和对比得到与郑达等[19]离心试验模型相似的CCM。基于以上模型及参数，研究边坡倾倒破坏的演化过程，分析边坡的层间应力分布特征。最后，探究层间剪切强度对边坡岩层初始折断位置、垮塌范围、破裂面倾角的影响，简要探讨岩层层厚对滑坡最终形态的影响。

1 边坡数值模型

1.1 黏聚力裂缝模型(CCM)

1.1.1CCM基本原理

如图1所示，黏聚力单元将材料界面分离破坏的过程用实体单元两个面之间的“相对分离位移-力”关系表达，这种关系被称为牵引-分离准则[20-21]。该准则定义了黏聚力单元的力学行为，适用于内部存在黏结作用的材料(岩石、混凝土等)，将0厚度的黏聚力单元插入实体单元后构成CCM，此模型通过黏聚力单元的删除，较准确地模拟岩石的断裂行为。该准则假定沿着破裂面的法线方向存在一个牵引力σn，沿着破裂面的切线方向存在两个牵引力σs、σt，这些牵引力随破裂面相对位移的增加，先增大后减小。当这些牵引力减小至零时，单元删除。

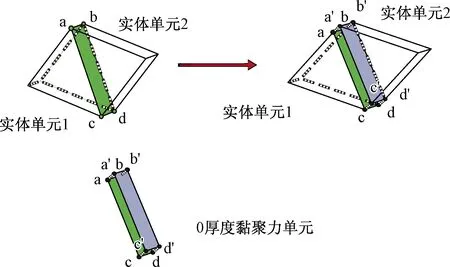
图1 黏聚力单元示意图Fig.1 Schematic diagram of the cohesive element

本文采用如图2所示的混合型牵引-分离准则定义节理面以及岩层内的零厚度黏聚力单元。其中tn0、ts0、tt0、tm0分别为黏聚力单元达到初始损伤时的法向应力、剪切应力以及混合模式的应力，δn0、δs0、δt0、δm0分别为黏聚力单元达到初始损伤应力时所对应破裂面法线方向、剪切方向及混合模式方向的相对位移，δnf、δsf、δtf、δmf分别为黏聚力单元失效删除时所对应的破裂面法线方向和剪切方向的相对位移以及混合模式方向的相对位移。定义损伤因子D(0≤D≤1)来表示黏聚力单元损伤过程的发展，在黏聚力单元达到初始损伤强度后，损伤因子D的值从0开始逐渐增加，当损伤因子D的值达到1时黏聚力单元被删除，岩块发生断裂。

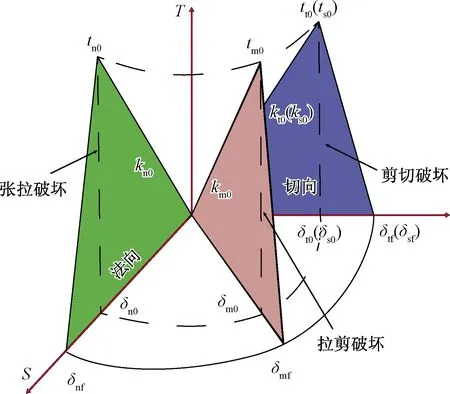
图2 黏聚力单元破坏模式Fig.2 Failure mode of the cohesive element

显然，这个过程也是单元刚度衰减过程。黏聚力单元三种破坏模式下的应力损伤关系式为：

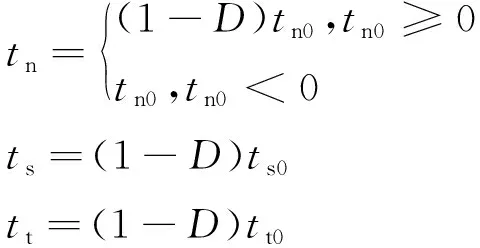
(1)

式中：tn——黏聚力单元法向应力；

ts、tt——黏聚力单元切向应力。

黏聚力单元损伤演化过程中的法向及剪切刚度可表示为：

kn=(1-D)kn0

ks=(1-D)ks0

kt=(1-D)kt0

(2)

式中：kn——黏聚力单元法向刚度；

ks、kt——黏聚力单元切向刚度；

kn0——黏聚力单元法向初始损伤刚度；

ks0、kt0——黏聚力单元切向初始损伤刚度。

对于混合模式下黏聚力单元损伤演化，使用等效总位移来描述，可表示为:

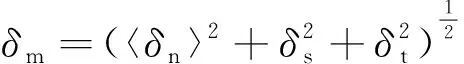
(3)

式中：〈〉——Macaulay括号(当δn>0时〈δn〉=δn,否则〈δn〉=0)；

δn——破裂面法向相对位移；

δs、δt——破裂面切向相对位移。

损伤因子D在损伤演化阶段应满足以下关系：

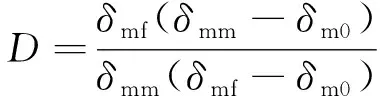
(4)

式中：δmm——加载过程中允许的最大位移。

黏聚力单元在损伤演化过程中应当遵循最大主应力原则，该原则可以表示为：

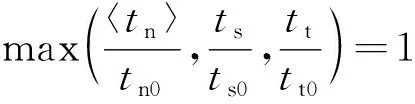
(5)

式中：〈〉——Macaulay括号。

如图2所示，根据黏聚力单元面法向牵引力tn和切向牵引力ts、tt与其对应方向的初始损伤强度tn0、ts0、tt0之间的关系以及其组合公式，大致分为以下三种破坏模式：

①若沿着单元面的法向牵引力tn先达到初始损伤强度tn0，那么单元最终的破坏模式则为张拉破坏；

②若沿着单元面剪切方向切向牵引力ts、tt先达到与其对应的初始损伤强度ts0、tt0，那么单元最终的破坏模式则为剪切破坏；

③如果符合式(6)，那么最终的破坏模式则为拉剪破坏。

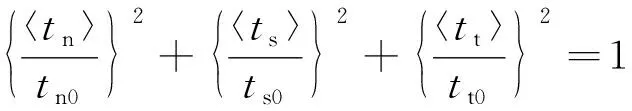
(6)

层状岩体中的节理面和岩层内的岩块之间都考虑这三种破坏模式。

1.1.2CCM构建过程

由于通过ABAQUS软件的界面操作在每一个实体单元间插入0厚度黏聚力单元是困难的，因而需要借助程序对有限元模型进行前处理。首先建立原始几何模型并划分网格，导出模型文件。之后通过MATLAB程序对模型文件中单元编号以及节点坐标进行更改，大致思路如下：

①将原始模型中相同的节点分别赋予两个不同的序号，目的是将单元进行离散，为零厚度单元的插入做准备；

②将产生的新编号的节点数据以及开裂区单元节点的变化添加到模型文件中；

③添加黏聚力单元的数据信息，即在源文件的关键字中声明单元类型的更改；

④为这些新加入的单元设置材料和截面属性并再次导入ABAQUS中进行边界条件等的设定。

1.2 反倾层状岩质边坡CCM建立

1.2.1数值模型信息及加载

将3 586个零厚度黏聚力单元嵌入到2 455个实体单元之间，并根据离心机模型(图3)按1∶1比例构建相对于边坡的CCM(图4)。模型尺寸为800 mm×670 mm，岩层倾角70°，层厚15 mm；模型分阶段开挖三次，开挖坡比均为1∶0.18，开挖后坡脚均为80°，模型Z方向仅划分一层单元并约束模型所有节点在厚度方向上的自由度。郑达等[19]在试验过程中并未使用机械手在离心机转动时进行开挖，而是将离心机停转后通过人工手段实现开挖工况。为保证离心机试验模型和相应的数值计算模型在开挖条件上一致，数值模型加载过程如下：

通过“单元杀死”模拟开挖条件，将原始边坡稳步加载至120g，稳定转动1 200 s后，加速度降至0g，进行第一级开挖；再稳步加载至120g，如此往复直至第三级开挖。

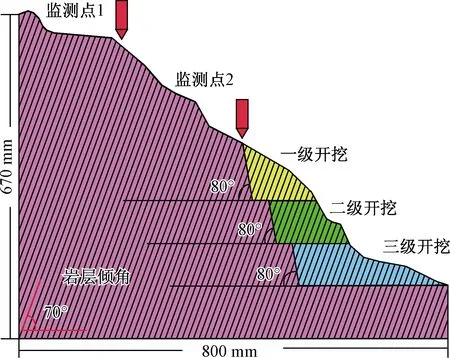
图3 离心机模型示意Fig.3 Centrifuge model

1.2.2黏聚力裂缝模型中的时间

使用ABAQUS中Dynamic、Explicit分析步进行计算，此分析步为基于动力学方程的动态显式算法。此算法中时间即为运动方程中的时间，是真实时间。模型设置的最小时间步长为0.01 s，并通过定义幅值曲线的方式对加速度时程曲线进行输入。

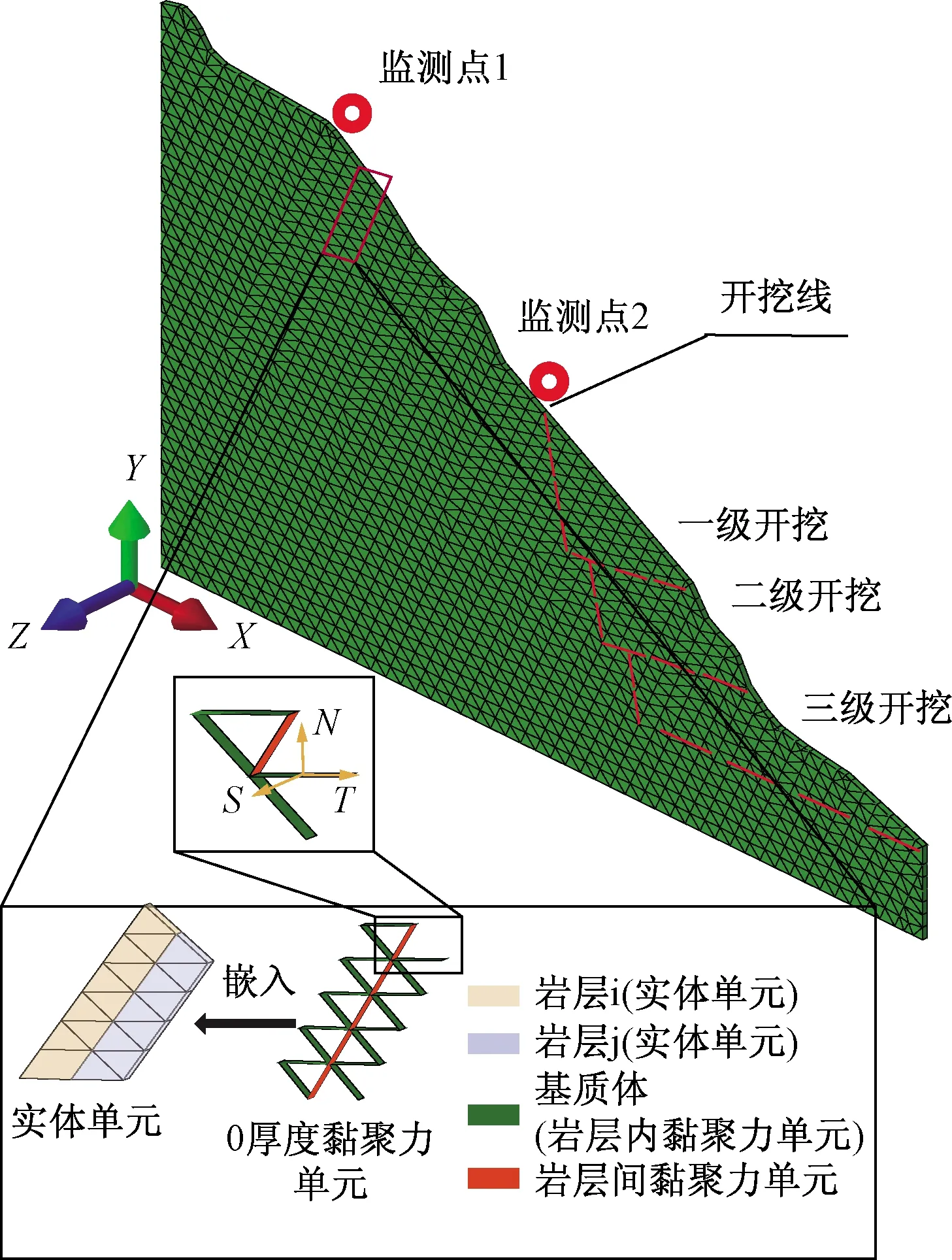
图4 黏聚力裂缝模型Fig.4 Cohesive crack model

1.3 黏聚力裂缝模型参数及标定

如图4所示，模型中的黏聚力单元按嵌入位置不同，分为在岩层之间的层间黏聚力单元与岩层里的基质体(非层间黏聚力单元)。由于CCM模型属细观唯象模型，其参数不具备严格的宏观物理意义，因而需要与试验进行标定和对比，以确定黏聚力单元的具体参数。如果经标定和对比后的CCM模拟结果与试验结果基本吻合，那么就可以认为模型建立两者相似[16]，也就验证了CCM的正确性。具体标定过程如下：

(1)岩石材料及基质体参数标定

通过模拟抗压强度试验可以对基质体参数进行标定[16]。建立直径80 mm、高120 mm的圆柱形试件模拟抗压强度试验，与郑达等[19]给出的岩层试验材料的弹性模量和单轴抗压强度进行标定，得出基质体内的黏聚力单元参数(表1)。

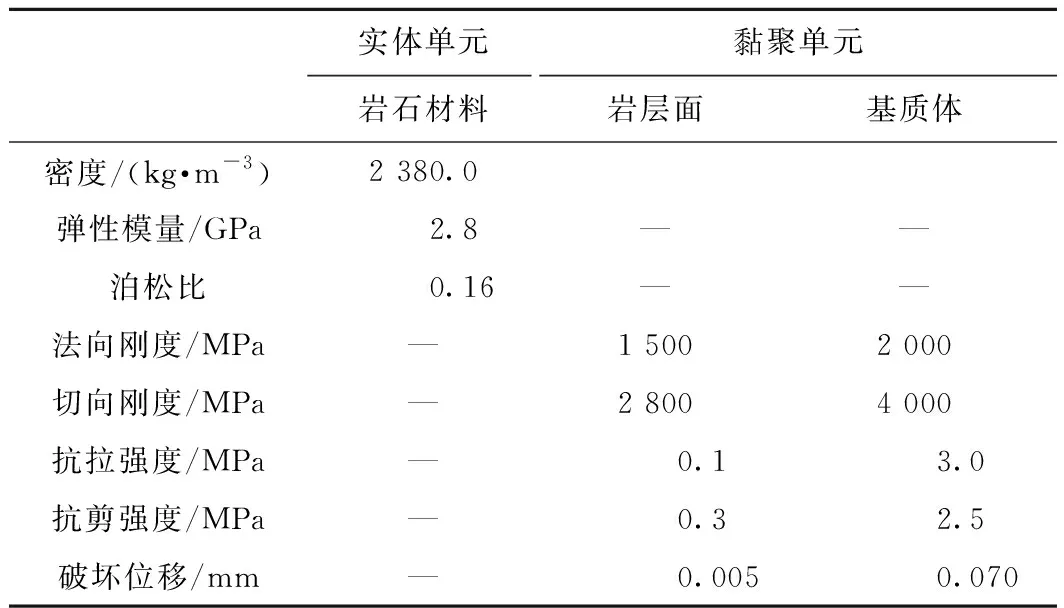
表1 数值模拟中各单元的力学参数

(2)岩层面参数标定

通过将数值模型监测点位移曲线与郑达等[20]离心机试验结果中的位移曲线进行对比(图5)，对CCM中的层间黏聚力单元参数进行校核，最终得到岩层面(岩层间黏聚力单元)参数(表1)。

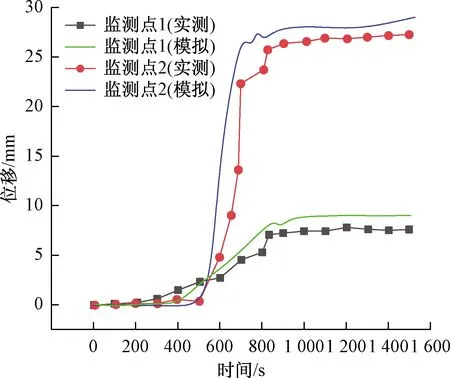
图5 位移的比较Fig.5 Displacement with time

2 数值模拟结果

2.1 数值计算与模型试验对比

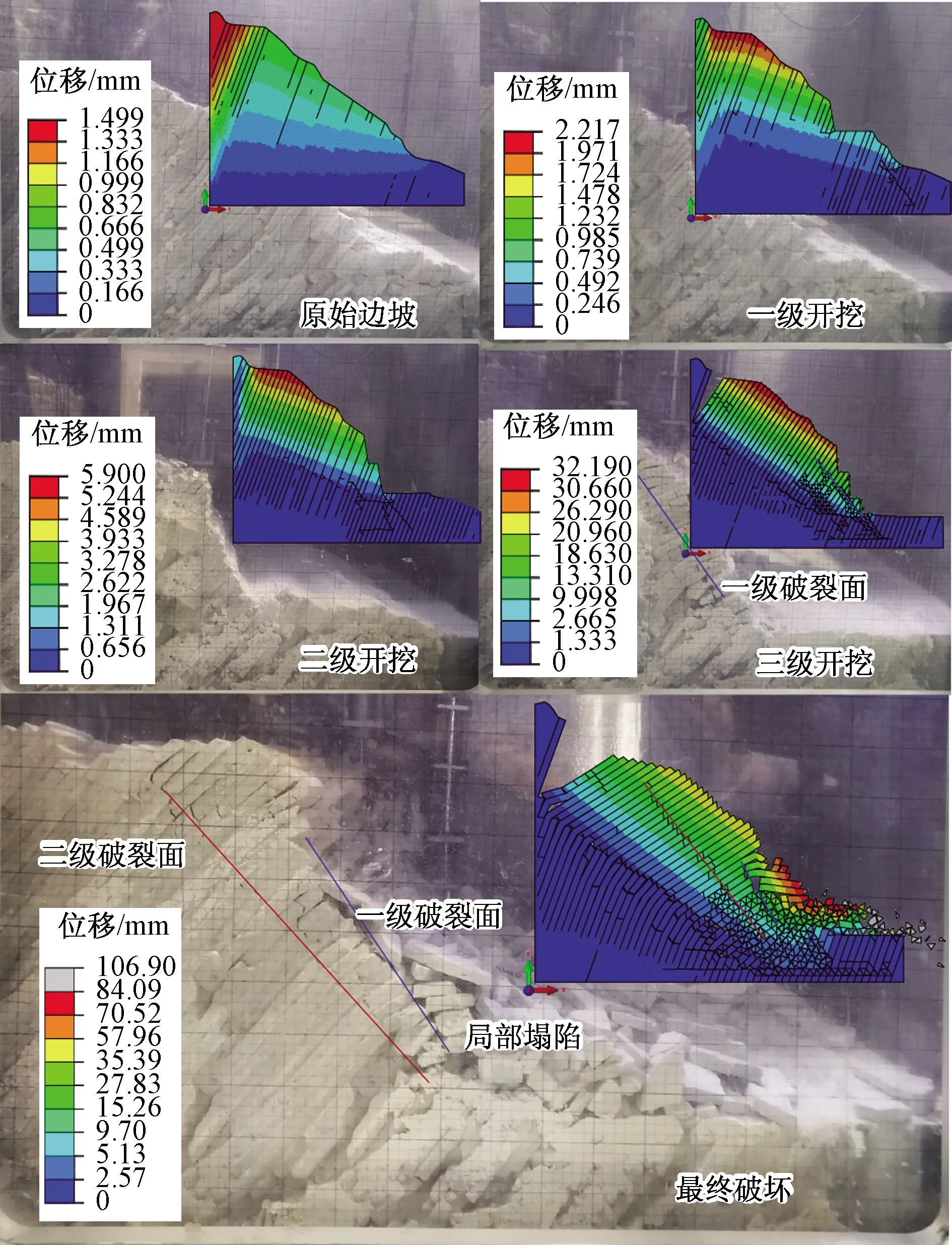
图6 倾倒变形特征的比较Fig.6 Comparison between the numerical toppling deformation and experimental results

图6表明在离心机试验模型及相应的数值计算模型中，各阶段的坡体变形特征基本一致，验证了CCM的正确性。原始模型阶段，边坡并未产生明显变形，大多数的变形产生于自重下边坡顶部的沉降，且边坡后缘范围内层间发生较小的相对位移。一级开挖阶段，坡体后缘范围内的层间相对位移继续增加，岩体层间裂隙进一步增多，表现为坡体距表面约150 mm的断续裂隙，坡表岩体有向临空面“点头哈腰”倾倒的趋势，但未见倾倒。二级开挖阶段，延续上一阶段的变形，边坡表层岩体继续向临空面变形，层间相对位移较之前增大，层间裂隙发育更为明显。三级开挖阶段，较以上两阶段有明显变化，边坡岩层出现倾倒现象，坡体后缘拉开，边坡自坡脚至坡顶产生贯通破裂面，形成一级破裂面，且坡脚处出现局部垮塌。最终破坏阶段，坡表岩体沿一级弯折带发生失稳破坏形成滑坡，并同时出现二级破裂面，这说明了此方法在模拟层状岩体倾倒变形方面的合理性。

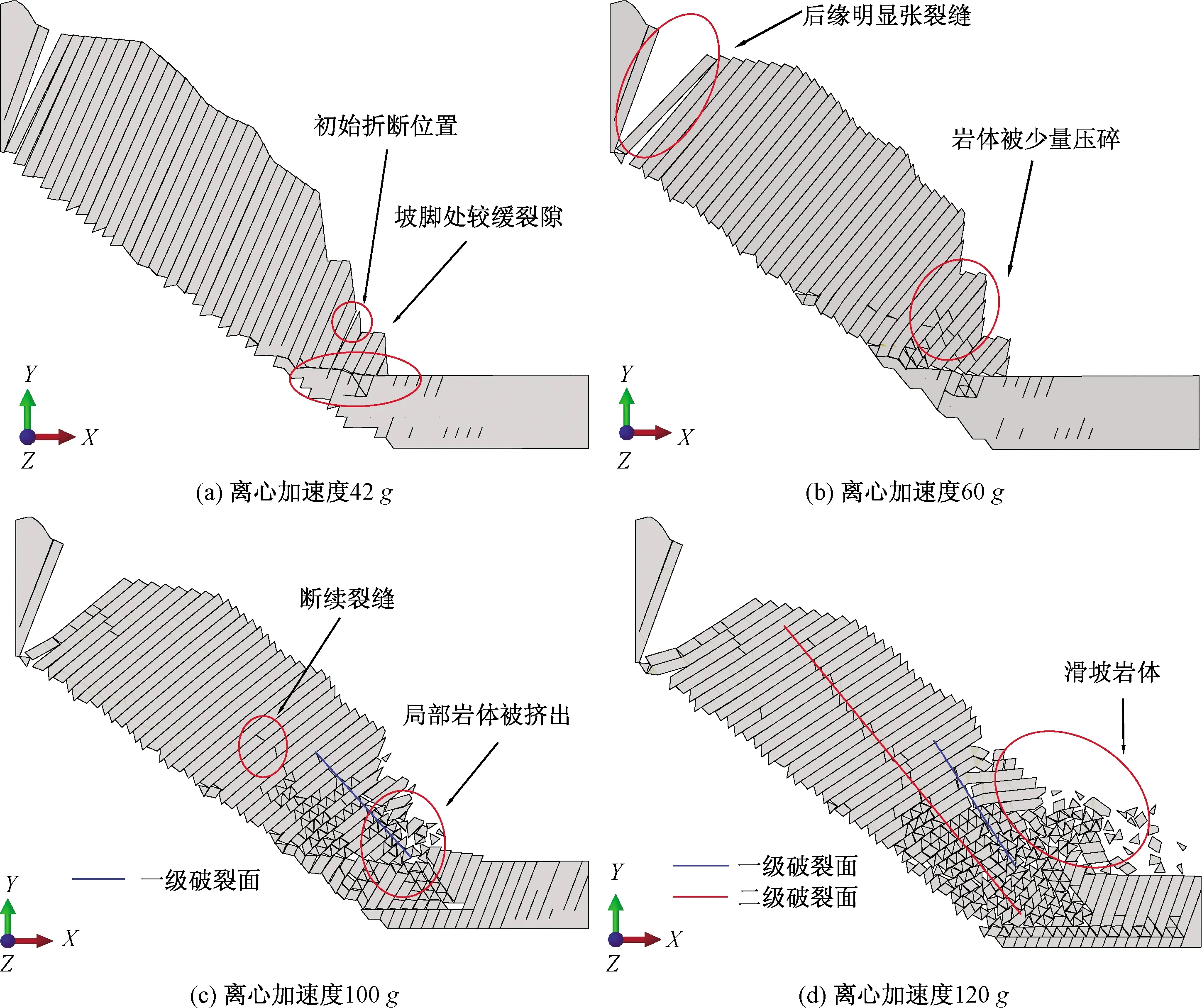
图7 演化过程图Fig.7 Picture of the evolution process

2.2 边坡破坏演化过程

由于原始模型阶段以及一级开挖、二级开挖阶段，坡体变形较小，因此本节只针对模型破坏演化主要发生的三级开挖和最终破坏阶段进行演化过程的分析，结果见图7。随着重力加速度的提高，坡体变形加剧，离心加速度达到42g左右时(图7a)，层间已发生明显错动，坡脚处出现一条较缓的近乎水平的破裂面，且出现初始折断，此时坡脚岩体并未压碎挤出。离心加速度增至60g左右时，距离坡体后缘约40 mm 处出现明显的张裂缝，坡脚处岩体被少量压碎但并未被大范围挤出，层间错动加剧(图7b)。离心机加速度100g左右，坡脚处岩体碎裂区域进一步扩大，层间错动进一步加剧，且局部岩体被挤出，破裂面进一步向坡顶方向扩展将坡体贯通，形成一级破裂面(图7c)。值得注意的是，随着层间错动的增加，深层坡脚破碎区萌生出距表层较远的断续裂隙，这说明二级破裂面正在发育。离心加速度达到120g左右时(图7d)，坡脚处的破碎岩体被大范围挤出，一级破裂面贯通形成滑坡，同时二级破裂面贯通。这说明，反倾边坡最终的破坏形式是沿着某条贯通的破裂面发生整体失稳破坏，且层间错动对破裂面形成有促进作用。

综上得知，反倾层状边坡的演化是一个动态过程：从坡脚处开始，坡脚处岩体断裂，随后坡体后缘出现张裂缝，使层间错动加剧，致使坡脚处岩体被碾碎挤出；而坡脚处岩体的挤出又反过来加剧了后缘的张开以及层间的错动，两者相互作用，最终导致滑坡灾害发生。综合原始模型阶段与一级二级开挖阶段模型的变形过程(图6)可知，坡体临空条件的改变是滑坡灾害发生的重要因素，开挖实质上是为坡体岩层发生层间错动提供了变形空间。坡体的整个破坏演化主要分为两个时期：第一时期主要表现为临空条件改变导致的层间错动；第二个时期为边坡的倾倒变形破坏，主要表现为破裂面的发育。

2.3 边坡层间应力分布特征

以往的反倾层状边坡研究经常简化为叠合悬臂梁模型[22-23],因而岩体层间作用力特别是法向作用力的作用形式对于反倾层状边坡的破坏模式具有重要影响。

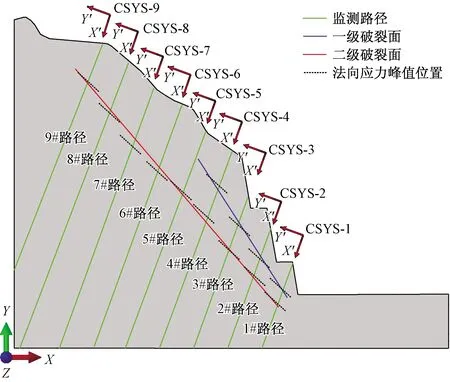
图8 监测路径示意Fig.8 Monitoring path

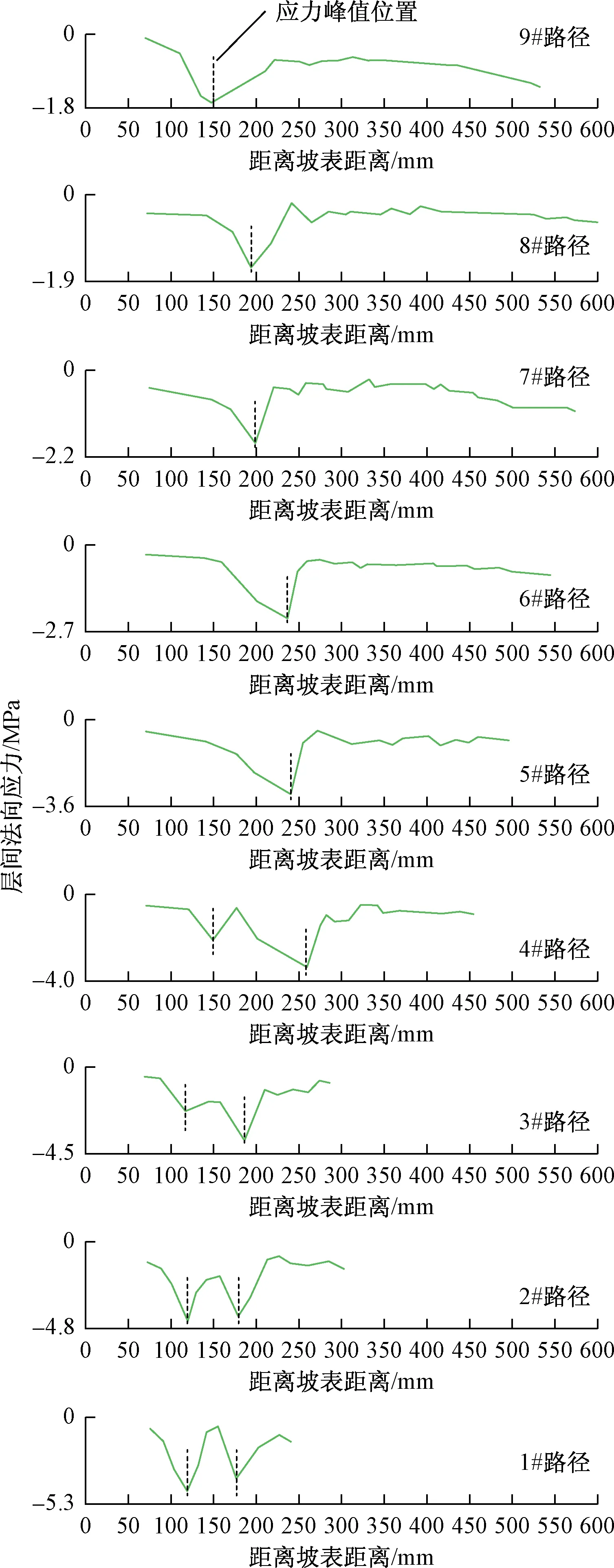
图9 层间法向应力图Fig.9 Normal stresses between layers

设定9个局部坐标系(图8)，基于每一个局部坐标系，设定数据提取路径，从坡脚至坡顶共9条，定义为1 #路径、2 #路径、……、9 #路径。离心机加载至100g时,破裂面接近完全贯通，提取此时各个监测路径上的层间法向应力绘于图9。如图所示，坡脚位置以1#路径为例，从坡体表面到坡底0～150 mm范围内，出现两个主要的法向应力峰值，且法向应力波动明显，随着距离的增加法向应力并未出现明显增加。坡体中部位置以4 #路径为例，从坡体表面至坡底 450 mm 范围内，出现两个主要的法向应力峰值，距离坡体表面约200 mm范围内应力波动较为明显,且沿着监测路径方向的深度的增加，应力未出现明显增长。坡体后缘以8#路径为例，从坡体表面至坡底550 mm范围内，仅出现一个主要的法向应力峰值，应力波动较小，且随着距离的增加，法向应力表现出不断增大的趋势。从路径应力峰值大小的角度进行分析，层间法向应力整体上呈现由坡顶至坡脚逐渐增大的趋势，这说明距离坡脚越近岩体破坏越严重。

此外随着坡高的增加，层间法向应力有向坡体内部增大的趋势，尤其是在8 #和9 #监测路径表现明显，产生此现象的主要原因是随着距离坡体表面深度的增加，岩体自重应力产生的法向分量增大。对各个监测路径中层间法向应力峰值出现的位置进行分析可知，坡脚处监测路径(1—4 #路径)有2个较为明显的法向应力峰值，而坡体中部与坡体后缘位置的监测路径(5—9 #路径)只有1个较为明显的法向应力峰值，且峰值的位置恰好对应1—4 #路径范围内的两条破裂面的位置。继续沿着坡顶的方向，将5—9# 监测路径法向应力峰值所在位置在坡体对应位置上标出，恰好就是破裂面的所在位置。也就是说，坡体的破裂面基本会沿岩层间法向应力峰值所对应位置的连线发育。

3 层间剪切强度对边坡破坏特征的影响

3.1 层间剪切强度对初始折断位置的影响

初始折断位置影响滑坡形态。为探究层间剪切强度对初始折断位置的影响，按不同层间剪切强度将模型分为a(0.25 MPa)、b(0.15 MPa)、c(0.05 MPa)三组，其他条件不变。将岩层初始折断时的位移云图绘制于图10。层间强度取0.25 MPa(a组)，岩层在t=650 s左右时发生初始折断，折断位置接近坡脚(图10a)。层间强度取0.15 MPa(b组)，岩层在t=550 s前后发生初始折断，折断位置接近坡体中部(图10b)。层间强度取0.05 MPa(c组)，岩层大约在t=450 s时发生初始折断，折断位置接近坡体后缘(图10c)。

由此可知，层间剪切强度不同，坡体初始折断时间和初始折断位置不同。随着层间剪切强度的增大，岩层初始折断位置自坡脚至坡顶逐渐升高。岩层初始折断时间随层间剪切强度的增大而延后。岩层层间抗剪强度越大，坡体发生初始折断时的整体位移越小。

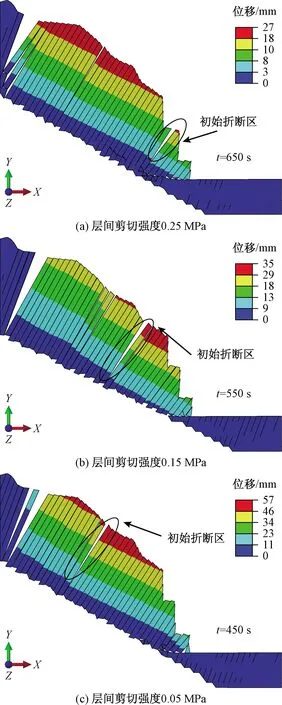
图10 不同层间剪切强度下位移云图及初始折断区位置Fig.10 Displacement and location of initial fracture zone under different shear strength between layers

3.2 层间剪切强度对滑坡形态及破裂面的影响

将不同层间剪切强度条件下模型的计算结果绘于图11。层间剪切强度为0.25 MPa时(a组)，岩层于坡脚处垮塌且边坡垮塌区域的范围较小(图11a)。层间剪切强度为0.15 MPa时(b组)，坡体下半段垮塌区域的范围与a组相比明显增大。层间剪切强度 0.05 MPa 时(c组)，坡体垮塌区域的范围进一步增大，发生整体垮塌(图11c)。分析得知，随着岩层层间剪切强度的降低，垮塌区域的范围由坡脚向坡顶逐渐增大，直至发生整体垮塌。

将图10所示初始折断区的位置在图11中对应标出，可以发现初始折断区的位置在垮塌区域上半段。这说明初始折断位置对滑坡形态影响明显，并且有一定预测作用。

在图11中，α和β分别为一级破裂面和二级破裂面与模型X正方向的夹角。由图11(a)可见层间剪切强度为0.25 MPa条件下破裂面的最终发育形态：一级破裂面和二级破裂面与X正方向夹角分别为116°和127°。图11(b)是层间剪切强度为0.15 MPa条件下的破裂面最终形态，α和β的值分别为130°和135°。图11(c)是层间剪切强度为0.05 MPa 条件下的破裂面倾角和位置，一级破裂面和二级破裂面与X正方向夹角分别为137°和146°。随着坡体岩层层间剪切强度的降低，破裂面与模型X正方向的夹角逐渐增大。与一级破裂面相比，距坡表更远位置的二级破裂面角度变化更为明显。

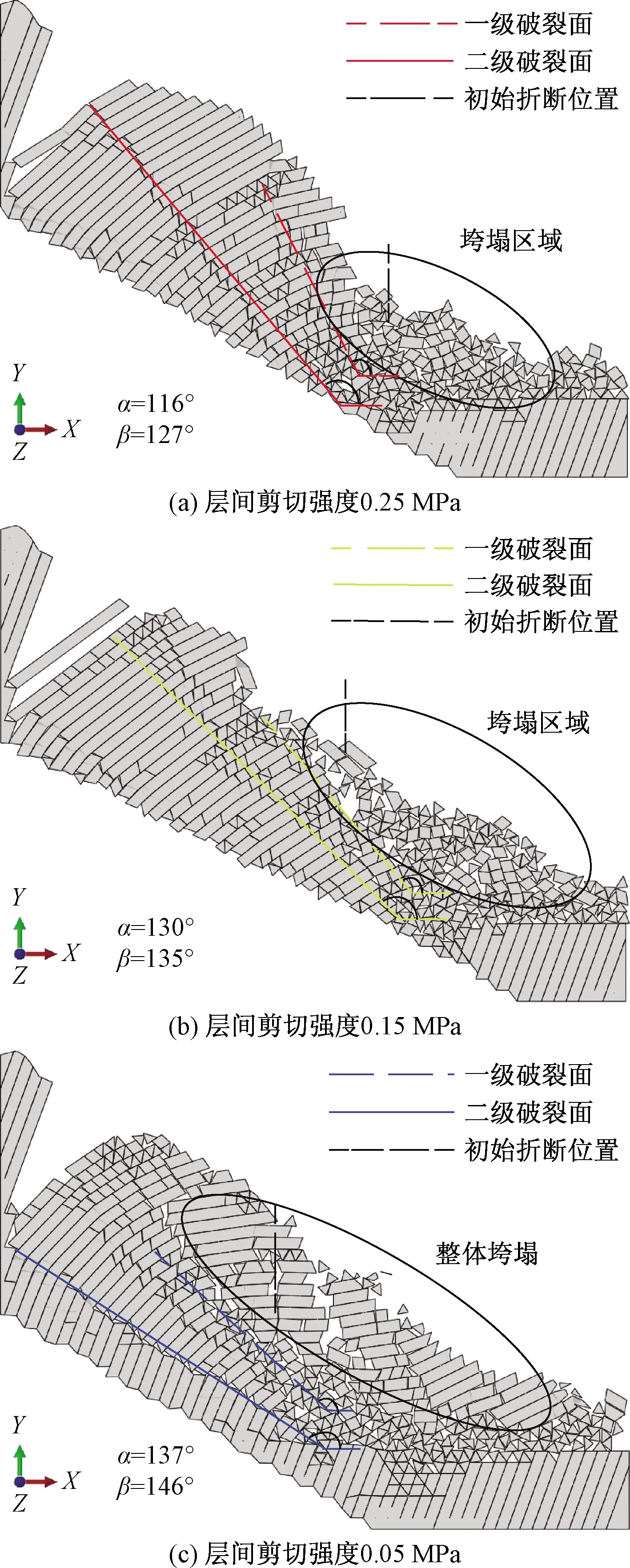
图11 不同层间剪切强度下滑坡形态Fig.11 Landslides under different shear strength between layers

4 讨论

岩层厚度对此类边坡的稳定性也具有较大的影响[11,23]。为探讨岩层厚度对反倾边坡滑坡形态的影响，分别建立含不同岩层厚度(10,15,20 mm)的反倾边坡模型并进行对比分析，岩层倾角和坡脚分别固定为70°和80°。图12给出了不同岩层厚度的边坡模型计算结果。结果表明：随着岩层厚度的增大，坡体由三级倾倒(岩层厚度为10 mm)逐渐整合成一级倾倒(岩层厚度为20 mm)，坡体的破碎程度逐渐降低，且一级倾倒破裂面逐渐向坡体深部发展。由此可见：岩层厚度越大，坡体的整体性增强；一级倾倒破裂面的深度越大，坡体倾倒部分提供的弯矩越大，说明了反倾边坡具有更大的抗弯承载力。

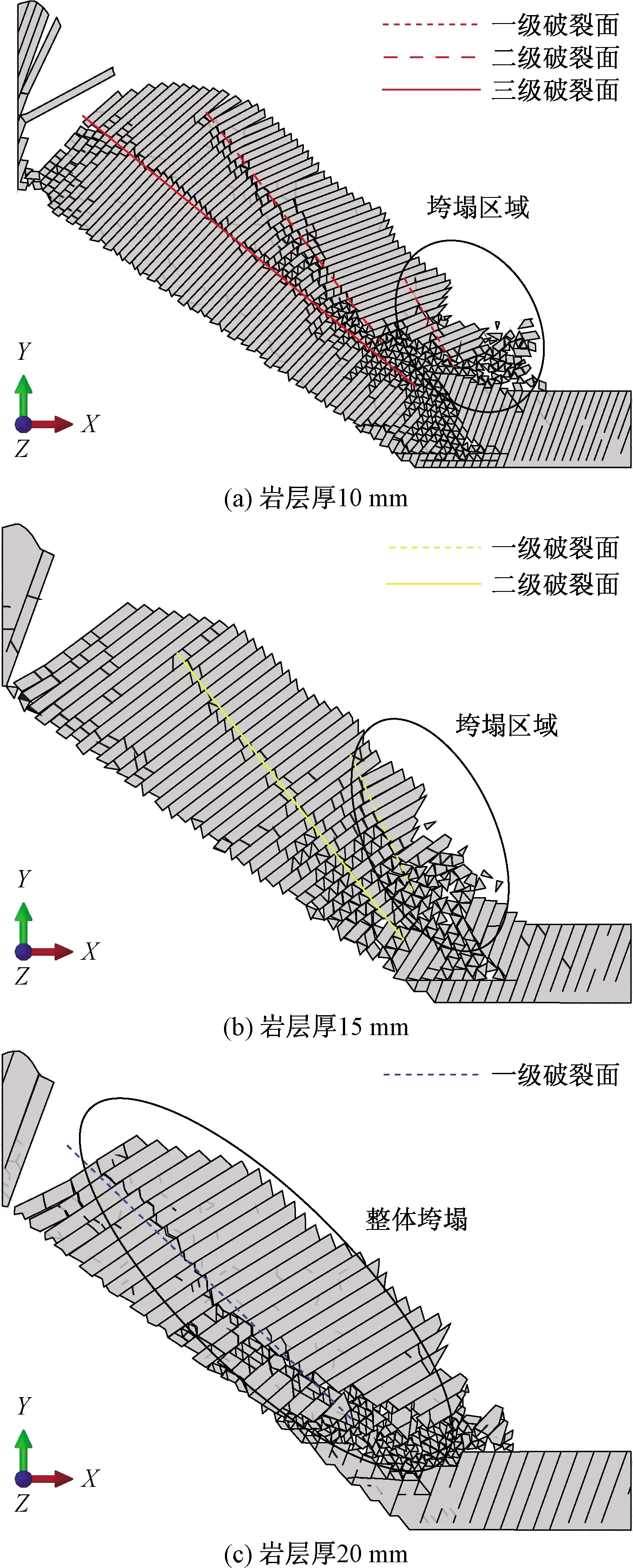
图12 不同坡体层厚下滑坡形态Fig.12 Landslides under different layers thickness

5 结论

(1)经过参数标定得到的CCM，能够与试验结果基本吻合，证明了CCM可用于层状岩质边坡的离心模拟分析，并能作为处理这类层状岩体边坡的有效计算方法。

(2)通过坡体演化过程的分析可知，反倾层状岩质边坡的演化是一个动态过程，岩层内部破坏是诱发滑坡的直接因素，层间相互错动加速岩层内部的破坏，而临空条件的改变则促进层间相互错动。

(3)破裂面位置可以通过监测层间法向应力获得，破裂面大致沿层间法向应力峰值位置的连线发育。

(4)层间剪切强度对坡体破坏形态影响显著，层间剪切强度越大，岩层初始折断区域越接近坡脚，岩层垮塌区域范围越小，破裂面倾角越缓。

(5)坡体层厚越大，坡体的整体性越强，抗弯承载力越大。