空间链接器式多维通用饱和-非饱和流模型研究

杨 海，姜月华，周权平，杨 辉，刘 林

(中国地质调查局南京地质调查中心，江苏 南京 210016)

土体中的多维饱和-非饱和流模型被广泛用于入渗过程中的水流运动模拟[1]和土体中的渗流问题[2-3]等，是非常重要的土体水分定量化计算工具[4-5]。早期建立的多维饱和-非饱和流方程称为改进的Richards方程，是基于单一水头(h)的方程[6]。该形式在非饱和流计算中有其局限性[7-8]，因渗流参数在时段内受毛管水头变化影响剧烈，易造成较大的质量守恒误差和对下渗深度的错误估算[9-10]。而利用水头(h)和土壤含水量(θ)构建的混合式方程在求解中可有效保证质量守恒[9]，因此成为最通用的多维饱和-非饱和流方程。在众多求解该偏微分方程的方法中，有限差分法因其简易方便而被广泛使用。

在以往的饱和-非饱和流模型中，每个离散单元需申请维度内最大可能连接单元数的系数存储空间[11](如三维中为6个)，而后根据单元与相邻单元间的连接情况计算各系数。当相邻单元为无效单元或相互间无水力联系时，系数为0。因此，该方法中难免会存储部分零系数，且零系数的规模随着边界单元、内部水力联系复杂度的增加而增加，这将极大影响模型在大规模网格单元中的计算效率。此外，当模型从高维度降至较低维度，计算时若维持最大可能连接单元数不变，则将产生更多零系数；但若减少最大可能连接单元数，则需修改局部代码。显然，这种建模求解方式并不高效、通用。因此，需要寻找合理的系数矩阵优化方法，在保证模拟精度的前提下，提高模型在大规模网格单元中的计算效率及通用性。

空间链接器(spatial linker)是指多维空间中有效计算单元间的虚拟链接，被用于记录两相邻有效单元间的连接关系。空间链接器式建模思路即预先分类提取不同方向(维度)上有效计算单元间的空间链接器，如此可避免产生零系数，节省数组存储空间，优化计算效率。该建模思想最早被用于大型河网水流计算中[12]，一维河道中的两控制节点利用链接器进行连接，而后又被推广至二维水流模拟中[13]。饱和-非饱和流数值模型中也出现过类似的思路，例如TOUGH2软件[14]中对无流量边界设置无流量连接，但尚未采用该通用模式进行整体性建模。陈景波等[15]曾在三维饱和-非饱和流建模中应用此建模思路，但模拟精度一般，且无法在复杂边界条件下应用，限制条件较多。因此，尚未有基于该建模思路对饱和-非饱和流模型开展通用化模式的探讨与研究。

本文针对多维饱和-非饱和流方程求解系数矩阵中常存在零系数的问题，提出在模型构建中预先记录有效单元间的连接关系(如连接方向、前后单元序号等)，避免计算和存储零元素，实现有效连接的压缩存储；并结合矩阵标识法，建立模拟精度较高的空间链接器式多维通用饱和-非饱和流模型。该项工作也旨在构建一套具有自主知识产权、可求解复杂多维饱和-非饱和流问题的程序。

1 模型构建

1.1 空间链接器及矩阵标识法

饱和-非饱和流方程的详细差分离散步骤可参考Dogan一文中[11]。所有非边界单元的方程组最终可写成如下矩阵表达式：

AH=R

(1)

式中：A——系数矩阵，具有主对角对称、高稀疏性特征；

H——当前时间步中的未知总水头矩阵，为单列矩阵；

R——常数项矩阵，为单行矩阵。

假设在n个有效计算单元中有m个链接，则方程中的非零系数个数为n+2m，其中n对应主元系数Ai,i的个数，2m则对应非主元系数的个数。链接器两端节点所记录的两非主元系数值相等且在矩阵中呈对角对称，即Ai,j=Aj,i。将系数矩阵A中的非零系数逐行存储于单行矩阵D中。定义空间链接器的数据存储结构为{istart, iend, d, a, b}，其中istart为首节点序号，iend为末节点序号，d为方向代号(0、1、2分别代表X方向、Y方向和Z方向，各方向均以靠近零点处为首节点)，a为首节点为主元时末节点系数Ai,j在矩阵D中的序号，b为末节点为主元时首节点系数Aj,i在矩阵D中的序号。多维中的链接器如图1中所示。

图1 空间链接器示意图Fig.1 Schematic diagram of spatial linkers

由空间链接器存储结构可知，建立空间链接器信息过程中，需对各计算单元进行编码。为适用于不规则边界区域和微地形环境，需进行两套单元的编码，即空间网格单元(包括有效单元和无效单元)及有效计算单元，且为便于地表边界条件设置，又需将有效计算单元分为地表单元和内部单元两类。以三维为例，离散网格单元按照自上而下、自前至后、从左往右的顺序进行编码，选取图2(b)中的DEM数据进行三维网格单元剖分，垂向离散尺寸为0.01 m，对单元及链接器进行编码，得到结果如图2(c)所示。4层剖分单元总数为24，但有效单元仅有12个，地表网格按顺序的存储编号为{1,3,4,7,11}，链接器共16个，其中x方向有6个([1]—[6])，y方向有3个([7]—[9])，z方向有7个([10] —[16])，依次记录空间链接器的数据存储信息。

图2 空间链接器与编码Fig.2 Spatial linkers and encoding

以空间链接器提前记录两相邻有效单元间的连接关系，实际上避免了不透水边界单元及无水力联系单元间的判断设置，仅需对非零系数进行计算和存储。设计多维方向代号可便于在多维度下进行拓展，模型更为通用。值得注意的是，空间链接器式建模方法需要在前期提取链接器信息，这将耗费一定时间，但随着单元数量的增多及边界条件复杂程度的增加，这部分耗时所占整体计算时间的比例将越来越少。

为更有效存储矩阵中的非零系数、提高后期求解效率，本文引入矩阵标识法，将原大规模系数矩阵写成简化的计算公式，其思想是将D中存储的主元、非主元系数分开记录。首先按行将系数矩阵A中的非零元素所在的列序号存于单行矩阵b数组中，然后将每行第一个非零元素在D中的序号存于单行矩阵J中，最后将每行主元系数在D中的序号存于主元标识k中。原始矩阵可改写成：

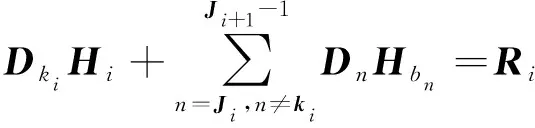
(2)

每个主元的水头值可使用非主元水头值表示：

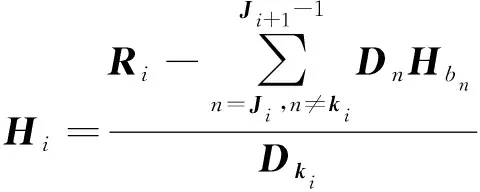
(3)

1.2 边界条件及模型参数

模型中考虑了三类边界条件，包括水头边界条件(Dirichlet)、流量边界条件(Neumann)及渗流面边界条件(Seepage face)，其中渗流面边界条件是一种混合型边界条件，每一时间步长中渗流面的实际位置需要通过迭代计算得到[16]。

求解饱和-非饱和流方程时，还需建立压力水头-土壤含水量(h)及压力水头-非饱和导水率K(h)之间的本构关系。压力水头与土壤含水量之间的关系被称为土壤水分特征曲线，选用经典的VG模型[17]对该曲线进行拟合，公式如下：

(4)

式中：m——经验形态参数，m=1-1 /n(n>1)；

θs——饱和含水率/(cm3·cm-3)；

θr——残余含水率/(cm3·cm-3)；

α——进气值的倒数/cm-1；

n——多孔介质的均一性。

非饱和导水率K(h)的确定采用van Genuchten基于Mualem模型提出的改进公式[17]：

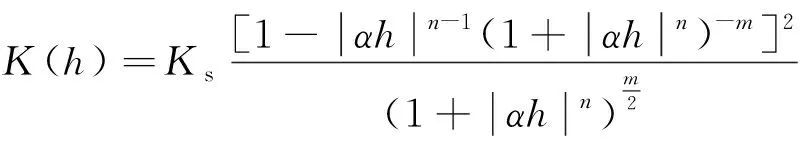
(5)

式中：Ks——饱和导水率/(cm·s-1)。

1.3 矩阵求解

模型中使用Intel®MKL函数库中提供的并行稀疏直接求解器(Parallel Sparse Direct Solver，PARDISO) 对生成的矩阵进行求解。该求解器是目前最快的线性稀疏矩阵求解方法之一，对于大规模计算问题，表现出极高的计算效率和并行性，也在FEFLOW[18]中被应用。求解中的收敛判断选用混合指标，即饱和带以压力水头的变化值进行判断，非饱和带则以土壤含水量的变化值进行判断。该模型在VS2008平台利用C++语言开发。计算机配置为Intel(R) Core(TM) i7-6500U(2.50 GHz)处理器、16 G内存。

1.4 误差分析

选取平均绝对误差(MAE)和均方根误差(RMSE)这两个指标统计不同模拟结果与实测数据之间的偏差，公式如下所示：

(6)

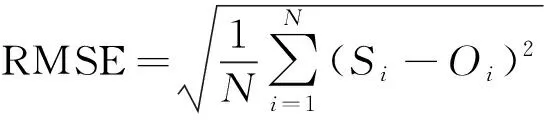
(7)

式中：Si——模拟值；

Oi——实测值；

N——样本数。

2 经典案例模拟验证

为检验模型在不同条件下的适用性及模拟精度，本文选取多维经典案例进行模拟。

2.1 一维非饱和入渗案例

选取文献[19]中的计算案例验证模型准确性。实验土柱的长、宽均为50 cm，高为200 cm，数值模拟中垂向离散成40个网格单元(z=5 cm)。地表输入雨强为50 mm/d，历时10 d，时间步长为0.1 d，如图3(a)所示。土柱中填充均质土壤，饱和导水率Ks=10 cm/d，孔隙度n=0.45(近似为饱和含水量)。土壤中的本构关系为：

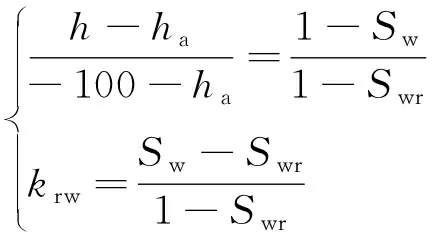
(8)

式中：h——压力水头/cm；

ha——进气压/cm；

Sw——饱和度；

Swr——凋萎饱和度；

krw——相对导水系数。

已知Swr=θr/n=0.333，ha=0，代入式(8)，则Sw=1+0.667h/100，krw=(Sw-0.333)/0.667。初始时刻底板处为地下水位(压力水头为0)，地表处压力水头为-90 cm (Sw=0.3997，krw=0.1)，其余地方均为-97 cm(Sw=0.353，krw=0.03)。计算后输出不同时刻沿深度的压力水头分布，与原文中的结果及UNSAT2模型[20]计算结果进行对比(图3b)。

图3 一维非饱和土柱边界条件示意图(a)和压力水头剖面分布(b)Fig.3 Boundary condition of the (a) 1D unsaturated soil column and (b) pressure head profiles for the unsaturated flow verification case

由图3可知，本文计算的不同时刻土柱垂向压力水头分布及变化过程与原文模型结果非常接近。以原文中的模拟结果为实测值，对比本文与UNSAT2的模拟结果误差(表1)。由表中可知，本文计算的各时刻、各深度处压力水头误差指标均小于UNSAT2。因此，本文提出的多维通用模型比UNSAT2模型更适用于一维非饱和带中土壤水分运动模拟。

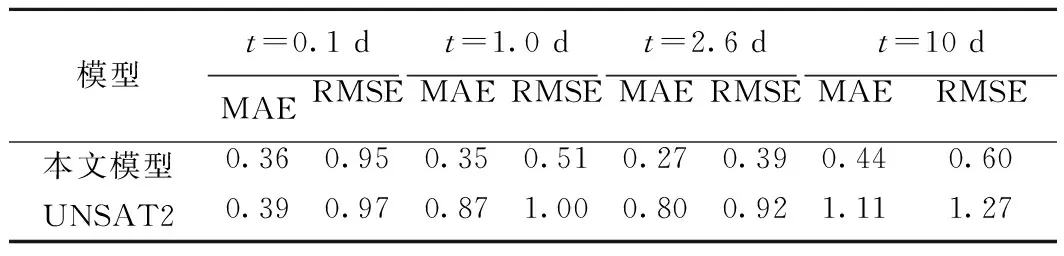
表1 模拟误差统计

2.2 二维及三维地下水位局部起涨案例

二维地下水位局部起涨案例选用Vauclin等[21]开展的实验，该案例被广泛用于验证饱和-非饱和地下水流模型的计算精度[22]。实验装置为填满砂土的600 cm×200 cm土槽，以槽底为零基面，初始水位65 cm。顶部中间100 cm宽度的土壤表面设置恒定补给流量R=3.55 m/d，其余区域封闭。因实验区域的几何对称性，仅需对一半区域(300 cm×200 cm)进行模拟，地表0～50 cm区间有稳定补给流量。离散网格单元中Δx=10 cm，Δz=5 cm，初始总水头H=h+z=65 cm，右边界单元为定水头边界，总水头恒为65 cm，底部为不透水边界。模拟时长8 h，时间步长Δt=1 min。已知储水率Ss=0，饱和导水率Ks=8.40 m/d，本文沿用Clement等[23]使用的VG模型参数，分别为θr=0.01 cm3/cm3，θs=0.30 cm3/cm3，α=3.3 m-1，n=4.1。因初始时刻表面土壤的含水量极低，前期计算时段内土壤含水量变化极快，因此需迭代150～250次才能得到较稳定、准确的数值解，水量平衡误差可控制在5%以内。模拟结果如图4～5所示。

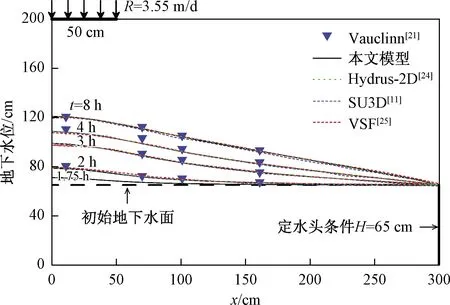
图4 不同时刻地下水位模拟值与原文中的结果对比Fig.4 Comparison of observed and simulated water table elevations at different times

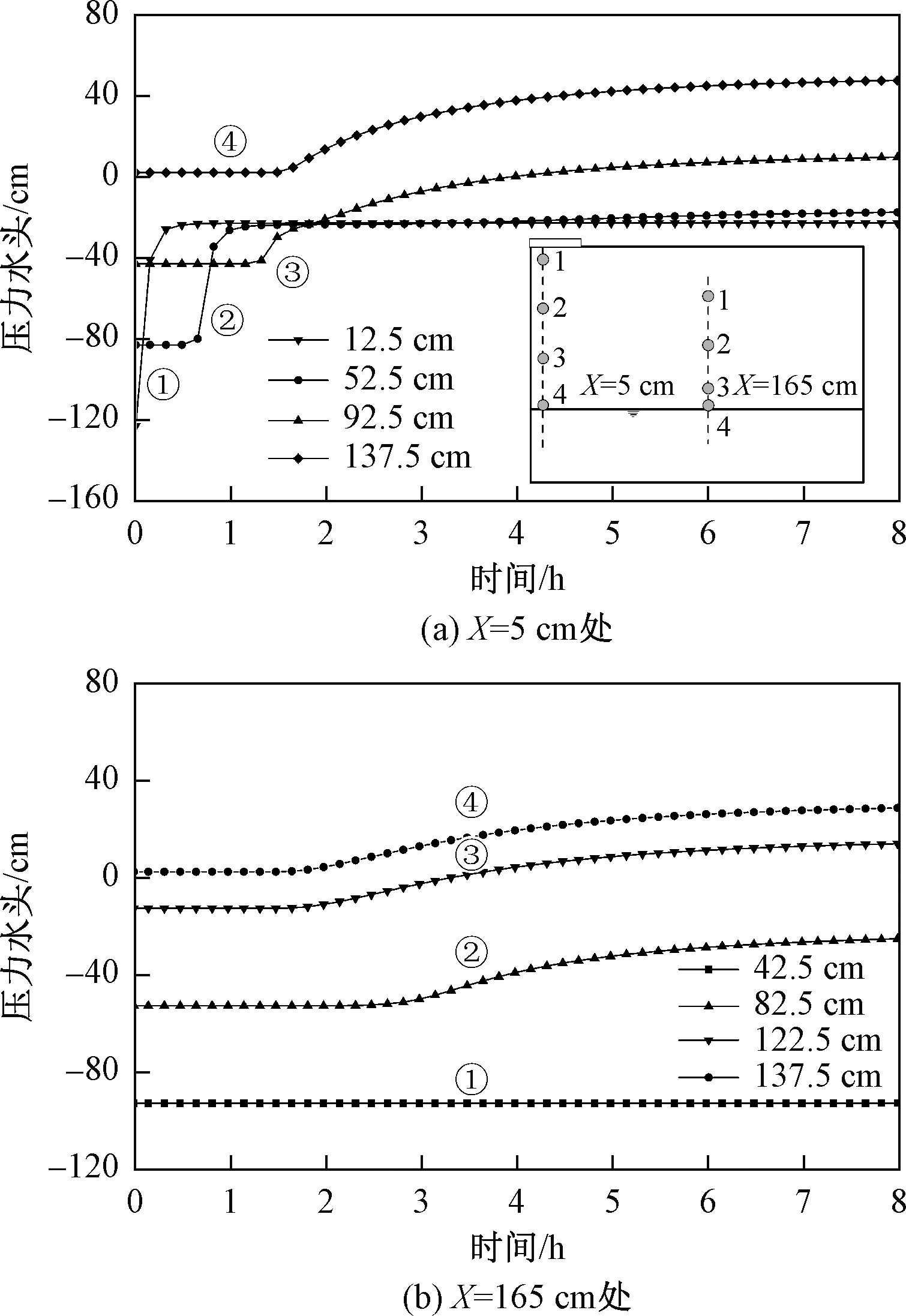
图5 不同深度的压力水头变化Fig.5 Changes in hydraulic heads with time at the different depths

由图4中可知，本文模型在不同时刻对比原文中的地下水位起涨过程拟合较好，补给区范围内的地下水位抬升最多，8 h后涨幅达55 cm，离补给区越远，地下水位涨幅越小。将本文模型同另外三种模型(Hydrus-2D[24]、SU3D[11]、VSF[25]模型)的模拟结果同Vauclin文中实测值比较，结果如表2所示，可知本文模型整体模拟精度与Hydrus-2D、SU3D、VSF模型基本一致。本案例在Hydrus-2D中的计算耗时为1.7 s，而在本文模型中的计算耗时为3.5 s。图5显示不同埋深处的压力水头变化，其数值变化过程与原文中结果基本一致。X=5 cm剖面处于补给区正下方，随着水量逐渐向下渗透，土壤中的压力水头沿埋深依次响应；而在X=165 cm剖面，土壤水更多通过饱和侧向流补给，因此越靠近地下水位，压力水头值越早发生变化，位置1处离地下水位最远，压力水头始终不变，说明此处没有受到水分的侧向补给。

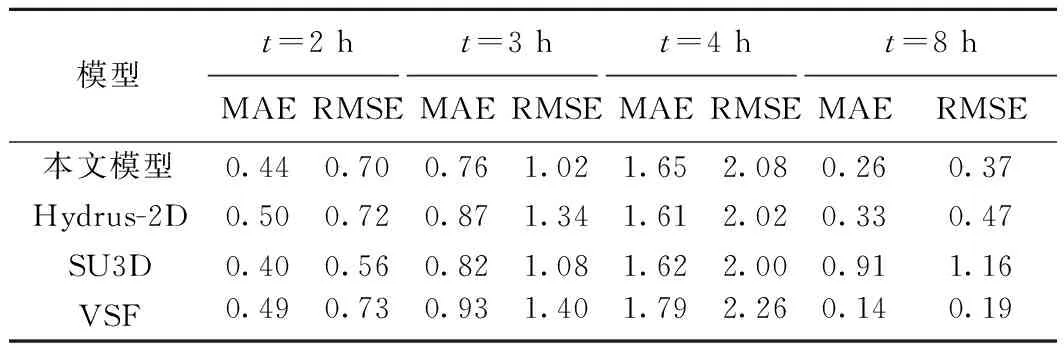
表2 模拟误差统计

将上述案例中的y轴向外延拓，即可升至三维空间进行模拟，令y轴方向上的区域长为300 cm，离散网格单元中Δy=10 cm，表面水量补给区域范围为50 cm×50 cm，保持其余条件、参数不变，最终的区域概况如图6(a)所示。选取y=0剖面，将不同时刻地下水面线输出，并与Dogan[26]博士论文中相同案例的计算结果进行比较(图6b)，并将8 h补给后的三维地下水面位置进行展示(图6c)。由图5(b)可知，稳定补给8 h后，y=0剖面补给区正下方的地下水面较之初始时刻上涨约15 cm，仅为二维案例中对应位置处涨幅的四分之一，可见扩展至三维后，补给区的水量向更多周边非饱和区域补给。与Dogan利用SU3D模型的结果相比，本文在0～100 cm范围内的地下水位模拟值略低于SU3D模型，最大差值约1 cm，但随着计算时间的增加，至8 h时两者的计算值已基本一致。本文t=8 h时的地下水面光滑平稳，较好地刻画了区域水头梯度及补给方向，较之陈景波等[15]模拟所得有明显突变的三维地下水面要合理很多。这些结果表明，本文模型的模拟精度与SU3D模型相当，优于陈景波等[15]提出的三维饱和-非饱和模型。

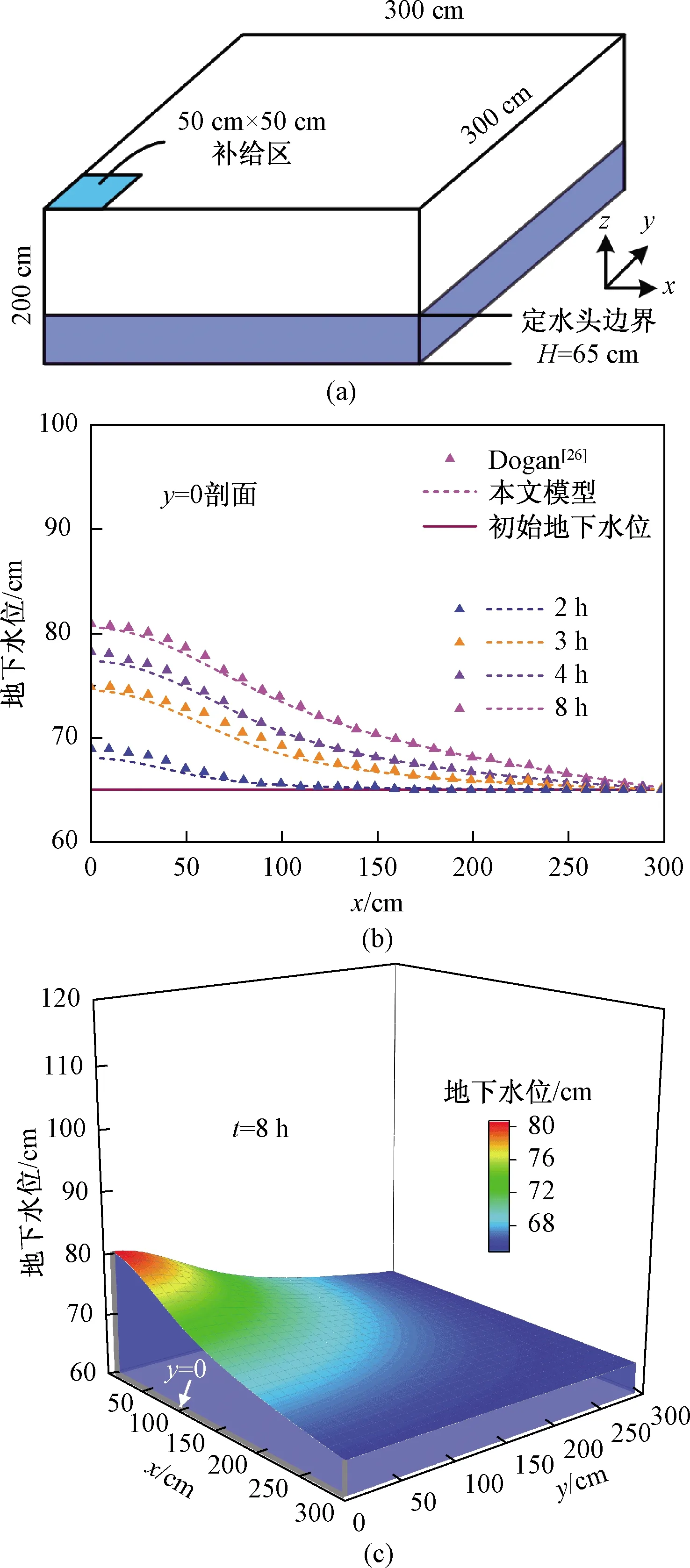
图6 三维模拟区域概况(a); y=0剖面处随时间变化的地下水面(b); 8 h补给后的三维地下水面(c)Fig.6 Description of (a) the 3D study area, (b) water table elevations at y=0 of various time and (c) 3D water table surface at the end of the rainfall

2.3 二维渗流面排水案例

为验证渗流面这一特殊边界条件的适用性，本文选取Vauclin等[27]于1975年设计的排水实验进行模拟，实验装置与2.2节二维地下水起涨案例中的一致。土槽中的初始地下水位为145 cm，右侧边界水位瞬间降至75 cm，随后下缘总水头稳定在75 cm。土柱中的地下水经右侧渗流面排水，整体地下水位逐渐下降至75 cm处。左侧及下部边界均设为不透水边界，右侧渗流面范围随地下水位下降而变化。模拟区域为300 cm×200 cm，离散网格单元中Δx=10 cm、Δz=5 cm，时间步长设为0.01 h。

使用原排水试验模拟中的Haverkamp关系式[28]及VG模型两套土壤本构模型进行结果比较。Haverkamp关系式中的土壤水分特征曲线及相对饱和导水率系数的表达式如下所示：

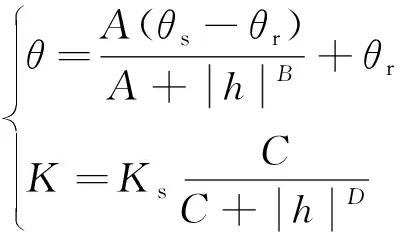
(9)

经对比多篇参考文献及模型结果验证，确定其中参数：A=4.0×104，B=2.90，θs=0.30，θr=0.0，C=4.0×105，D=4.5，饱和导水率Ks=9.6 m/d。VG模型中的参数与 2.2节一致。加入Hydrus-2D进行模拟对比，计算中的土壤本构关系选择VG模型。多个时刻的结果对比如图7所示。

图7 不同时刻模拟的地下水位和实测地下水位的对比Fig.7 Measured and simulated water table positions at different times

由图7可知，使用Haverkamp关系式(曾用于Vauclin 1975年模拟试验)的地下水位模拟结果略好于VG模型，VG模型在0.5 h后的计算水位均高于实测值，在5 h后与实测值及原文模型结果一致。由表3可知，不同时刻本文模型的模拟精度与Hydrus-2D相当。本案例在Hydrus-2D中的计算耗时为2.1 s，在本文模型中的计算耗时为4.5 s。本文模型可较准确定位渗流面的边界位置，可有效用于土体渗流问题的模拟。同时也发现，所选择的土壤本构模型及参数对土壤中模拟变量的分布影响极大。

表3 模拟误差统计

3 田间降雨入渗过程验证

3.1 研究区概况及参数测定

选取常州金坛区朱林镇红旗圩村一片稻麦轮作田进行采样、监测，并开展田间入渗模拟。区域地下水位埋深较浅，年内平均埋深仅55 cm。土壤为脱潜型水稻土，剖面呈现分层特征：0～13 cm为耕作层(A)，13～27 cm为犁底层(Ap)，27～54 cm为渗育层(P)，54～75 cm为潴育层(W)，75 cm以下为潜育层(G)。其中0～60 cm深度主要为粉质黏壤土，下层60～140 cm 为粉质黏土。区域内设立土壤水分监测剖面，在10 cm、20 cm、40 cm、60 cm和80 cm处埋设土壤水分探头，各层利用环刀取土样测定干容重，0～10 cm、10～20 cm埋深处土壤干容重分别为1.20 g/cm3和1.23 g/cm3，20～40 cm、40～60 cm、60～80 cm埋深处土壤干容重均值在1.46 g/cm3左右，显然表层土壤较之下层更为疏松。区域内还建有气象站与地下水位观测井，详见图8。

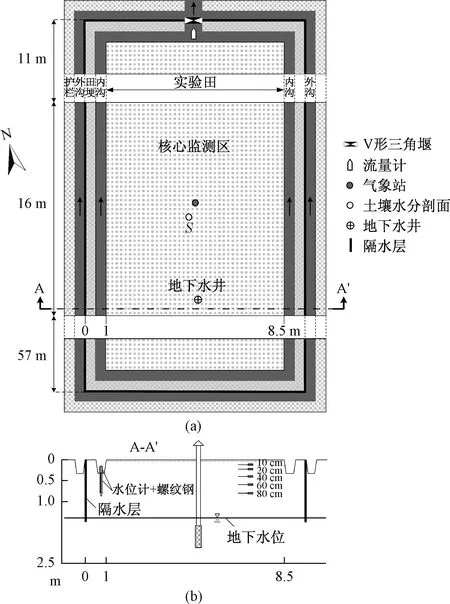
图8 实验区布局概化图Fig.8 Layout of the experimental area

田间各层土壤的水力参数、渗透性能各不相同，需要确定不同埋深处土壤水分运动参数的量级范围。本文在田间3个剖面(0～10 cm、10～20 cm、20～40 cm、40～60 cm、60～80 cm)5个埋深范围内采土样测定参数。对比采样层和土壤发生层埋深范围发现(表4)，第1、2、3采样层范围与对应的土壤发生层范围重合较多，此三层测量参数可代表土壤发生层内参数；第4、5采样层与对应的土壤发生层范围虽然错位较多，但仍有局部交集，采样层内实测参数值可近似代表对应发生层中的参数。利用压力膜仪法测定土壤水分特征曲线，定水头法测定土壤饱和导水率。以土壤吸力为 0 m 所对应的含水量为饱和含水量；吸力为150 m所对应的含水量为凋萎含水量。利用RETC软件估算VG模型中的参数，测得的各参数如表4所示。由表可知，VG模型中的参数变异性不一：各土层的θs均一性相对较好；θr和n在20 cm以上均一性较好，而在20 cm以下变异性明显大；α值变化最为敏感。各层饱和导水率的变异性也较大，并随埋深逐渐增大，至60 cm以下逐渐减小，这可能与土壤质地的变化有关。

3.2 参数敏感性分析

由式(4)、(5)中可知，土壤水分特征曲线受VG模型参数影响[29]，非饱和导水率则受α、n及饱和导水率影响[30]。因这两个公式极其关键且均呈现高度非线性，为便于后期案例中的参数率定，本文选用扰动分析法[31-34]对公式各参数进行敏感性分析，即在不改变其他参数的前提下，将单一参数增加或减少一定比例。选取一组原始参数值：θr=0.09，θs=0.465，α=0.01，n=1.25，Ks=0.09，单位与表4中一致。对土壤水分特征曲线公式各参数加入±5%的扰动(-5%即原参数值乘以0.95的系数)，对非饱和导水率公式各参数加入±5%、±10%的扰动，对比结果如图9所示。由图可知，n的扰动对土壤水分特征曲线的影响最大，其次是θs和θr，α影响最小；n的扰动也对非饱和导水率影响最大，其次是α，Ks的影响最小。因此，需要优先对n进行率定调试。

3.3 参数率定及模拟结果对比

根据土壤发生层特征将土体分5层进行模拟，分别是：0～13 cm，13～27 cm，27～54 cm，54～75 cm，75～150 cm。利用相同机理的Hydrus-1D软件手动率定土壤水运动参数，忽略地下水出流，参数l统一设为0.5。选取表层土壤含水量变化较大的20160402次降雨模拟一维下渗过程中不同埋深处的土壤含水量。结合测量的参数范围及相似质地土壤中的参数量级，最终得到率定后的各层参数，见表5。

表4 实验区测定的土壤水力参数

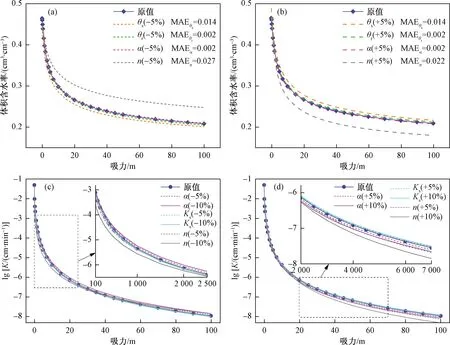
图9 参数敏感性分析Fig.9 Parameter sensitivity analysis注：(a)、(b)分别为VG模型参数加入±5%扰动对土壤水分特征曲线的影响; (c)、(d)分别为α、n、Ks三个参数加入±5%、±10%扰动对非饱和导水率的影响。

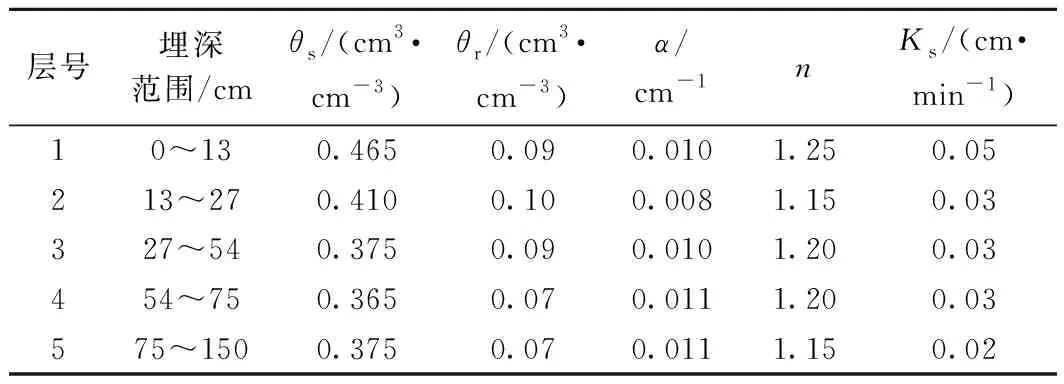
表5 率定的土壤水力参数

率定的VG模型参数大多在测定参数范围内，仅第1、2层的θr、α、n超出参数范围较多，这可能与田间三处采样剖面表层土壤的水力特性差异有关，表层土壤长期受人工耕作影响，疏松度不一，土壤水分特征曲线变异性较大，因此实测得到的参数范围也受到较大影响。率定后的Ks随埋深逐渐减小，均在测量值变化范围内。此外，次降雨中的表层土壤最大含水量与雨强呈正相关关系，更深处土壤层为地下水位频繁变动区，该范围内土壤最大含水量受地下水埋深影响。具体而言，当地下水位超过某位置时，该位置由非饱和态变为饱和态，最大含水量也有所升高，这可能与非饱和带土壤中滞留的空气有关。因此，在后期计算中需要根据次降雨实测的最大含水量调整模型中的饱和含水量，变动范围在0.04 cm3/cm3以内。

为验证各层率定参数的准确性，对各层单一参数加入相同比例扰动，对比土壤含水量模拟结果。因θs受实测最大含水量制约，θr仅对土壤水分特征曲线有所影响，因此选取n、α、Ks这三个参数进行扰动。考虑三个参数的敏感性差异，对n设计±5%的扰动，α设计±5%、±10%的扰动，Ks设计±10%、±20%的扰动，结果如图10所示。由图可知,n值的极小变化都对入渗过程影响极大，α在扰动达到10%时对20 cm和40 cm处的土壤水分变化过程造成一定影响，而设计最大扰动变化的Ks对含水量的变化过程影响最小。总体而言，所率定的各层土壤水力参数已达到较高的模拟精度。

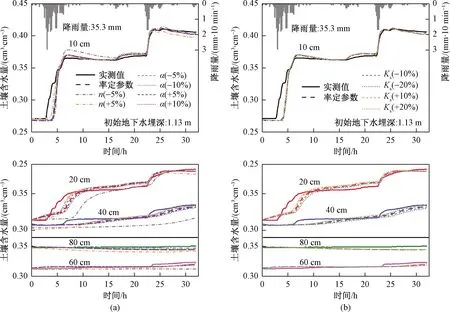
图10 土壤水力参数扰动对各层土壤水分模拟结果对比Fig.10 Comparison of simulated soil moistures of 5 layers using soil hydraulic parameter sets with some additional disturbance注：(a)为α、n扰动的影响; (b) 为Ks扰动的影响。

3.4 降雨入渗过程模拟

利用率定后的参数在本文构建的模型中计算，除率定的20160402次降雨外，又选取20160406、20160420次降雨进行模拟。各案例中根据地表植被茂密度，扣除降雨前期一定的植被截留量，忽略降雨入渗过程中的蒸发，得到结果如图11所示，其中图11(a)为表层40 cm以上(包括40 cm)的土壤含水量变化，图11(b)则为40 cm以下的变化。Hydrus-1D软件常用于模拟降雨入渗补给过程[35-36]，此案例中使用该软件计算结果和计算效率进行比较。经比较，本文模型模拟结果与Hydrus-1D软件中的结果十分相似，仅在60 cm、80 cm处略有差异。Hydrus-1D中三场次降雨过程计算耗时在0.4～0.8 s之间，本文模型中耗时约0.8～1.8 s，计算效率略低于Hydrus-1D。

图11 三场次降雨模拟的土壤含水量和实测值的对比Fig.11 Comparison of measured and simulated soil moistures of three rainfall events

由图11可知，整体而言，土壤含水量模拟值与实测值拟合较好，各深度处土壤含水量的绝对误差均小于0.03 cm3/cm3，可满足野外模拟的精度需求。在雨强相对较大的20160402和20160406次降雨中，表层40 cm以上模拟值的响应时间有明显延迟，这很可能与表层土壤中较多的大孔隙路径有关，在雨强较大时，部分水量通过大孔隙快速入渗。在初始地下水埋深相对较浅的20160420次降雨中，下层土壤水分的模拟也出现一定的延迟现象，这也暗示着大孔隙流可能会造成地下水位的快速响应，致使毛管边缘带中的土壤水分响应也较快，但变幅远小于表层土壤。此外，利用模型统计了3场次降雨末期(计算时间小于32 h)各埋深层中土壤水分增量，发现次降雨计算时段末期，超过80%的入渗水量仍滞蓄在表层40 cm的土壤中，其中0～10 cm土层中的土壤水分增量约为次降雨总入渗量的40%～50%，10～20 cm土层中约占总入渗量的20%～30%，20～40 cm土层则在20%左右，而转化为潜水的水量约占总入渗量的4%～12%，20160402次降雨潜水补给比例最小，20160406次降雨补给比例最大。

4 结论

(1)空间链接器式多维通用饱和-非饱和流模型利用多维方向上的空间链接器提前记录两相邻有效单元间的连接关系，避免了不透水边界单元及无水力联系单元间的判断设置，实现了系数矩阵的非零化计算和存储，并引入矩阵标识法以简化系数矩阵。

(2)选取地下水位起涨、渗流面排水等四个经典饱和-非饱和流案例验证模型模拟精度及效率，结果表明：该模型在多维度、不同边界条件(包括定流量边界、渗流面等)下的模拟精度与Hydrus、VSF等成熟软件相当，计算效率略低于Hydrus软件。

(3)对田间三场长历时小雨入渗过程进行一维概化模拟发现，VG模型中的参数n在率定过程中敏感性最强，各层土壤含水量模拟值绝对误差均小于0.03 cm3/cm3，结果与Hydrus软件基本一致。因模型中尚未考虑土壤中大孔隙流影响，各层土壤水分响应时间滞后于实测过程。三场次降雨计算时段末期，超过80%的入渗水量仍滞蓄在表层40 cm的土壤中，仅有4%～12%的水量已转化为潜水。

本文模型被证明是求解多维饱和-非饱和流问题的高效工具，有望成为传统多维饱和-非饱和流模型的重要补充。该通用化建模思路也非常适合将地表水、地下水模块进行耦合。然而，记录空间链接器信息时需循环遍历所有离散单元，该部分前处理过程不可避免地增加了一定存储空间和计算耗时。此外，模型中仅支持固定时间步长求解计算，这将增加简单边界条件下的计算耗时，未来仍需加入变时间步长计算方案，优化计算效率。