Dupuit模型的改进
——具入渗补给
陈崇希
(中国地质大学(武汉)环境地质研究所,湖北 武汉 430074)
1 研究背景
本文所述的Dupuit模型[1]是1863年最初提出的模型,即“圆岛状含水层稳定井流模型”[2],而非“无界含水层中影响半径稳定井流模型”,即方程中的R是圆岛半径, 而非影响半径。后者的地下水流是不可能形成稳定状态的[2-3]。
经典的Dupuit潜水稳定井流模型(1863年),只有侧向的圆岛外边界(湖海)及抽水井井壁内边界,而不涉及上边界降水入渗补给。如此一旦抽水,经过一定时间之后必导致海(湖)水入侵。然而自然条件大多存在大气降水的入渗补给,这样一来,Dupuit模型基本上只能在旱季用于地下水井流试验求取含水系统的参数,而不能够用于预测。人们往往企望截取大气降水补给地下水的开采模式,然而经典的Dupuit稳定井流模型却没有这个功能。就此而言,这是一个非常大的缺憾。
本文试图发展上述Dupuit圆岛状含水层稳定井流模型,即考虑地面入渗补给(蒸发排泄视为其负值)作用。如此,可用新建模型来预测相应条件的地下水开釆、排泄的效果。
所讨论的问题为稳定均匀入渗的条件,其它条件与Dupuit圆岛状潜水含水层井流模型相同。
2 解析模型的建立
2.1 假设条件及基本方程
(1)假设条件
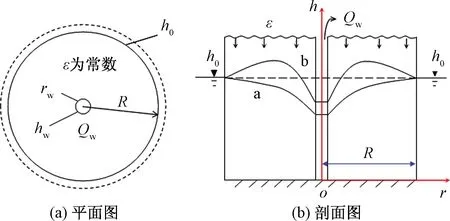
图1 具入渗补给的圆岛潜水稳定井流模型Fig.1 Steady well flow model of phreatic water in Round Island with infiltration recharge a—ε=0条件下的Dupuit下降漏斗曲线;b—ε>0条件下的漏斗曲线
隔水底板水平的均质圆岛状潜水层,上边界具稳定均匀入渗补给,外边界是定水位条件,抽水井位于圆岛中心。此条件下,地下水为径向(轴对称)稳定流,以潜水层底面为基准靣,取柱坐标系统(图1),且以井心隔水底面处为原点;由于地下水动力学井流中的流量通常定义抽水流量为正值,故记流速向井(原点)为正。
(2)基本方程
依水量守恒原理,假定渗流服从Darcy定律并满足Dupuit徦定,任一r断面的流量Q的计算公式为:
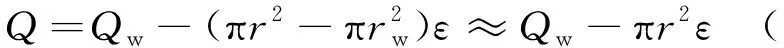
(1)
QR=Qw-πR2ε
(2)
式中:rw——井半径;
R——圆岛半径;
Qw——抽水井流量;
ε——入渗强度(单位时间单位面积入渗水量)。
若Dupuit假定成立,则任一断面流量Q为:
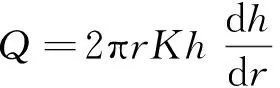
(3)
式中:K——渗透系数;
h——潜水位(等于潜水层厚度)。
2.2 流量方程及物理意义
(1)流量方程
将式(3)代入式(1),得
积分后得
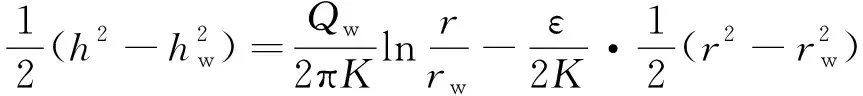
(4)
得
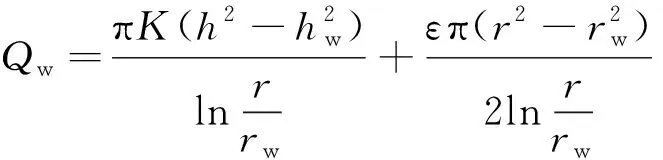
(5)
若取r=R≫rw,则h=h0,上式可改写为:
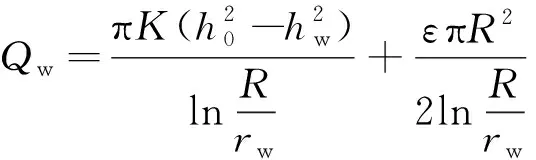
(6)
(2)物理意义
Qw由两部分组成:第一部分即无入渗补给条件的Dupuit流量方程,表示内外边界对Qw的贡献;另一部分表示入渗补给对Qw的贡献。
将式(6)代入式(2),得外边界的流量为:
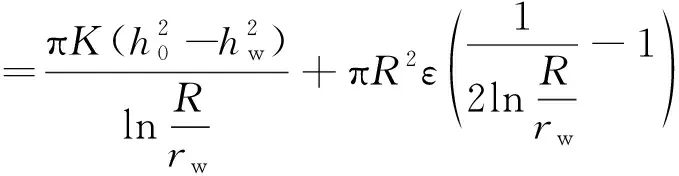
(7)
若QR>0,则外边界补给地下水(水位面如图1中的a曲线);若QR=0,则外边界与地下水间互不补排;若QR<0,则外边界排泄地下水,这时存在地下水分水岭(水位线如图1中的b曲线所示)。
将式(6)代入式(1),得任意断面的流量:
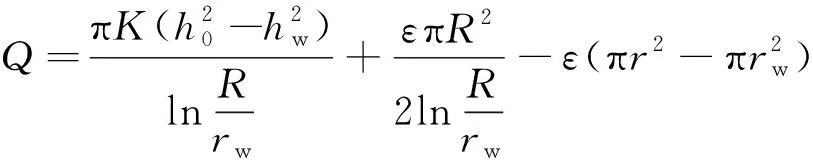
(8)
2.3 水位方程及地下水分水岭
(1)水位方程
由式(4)整理得
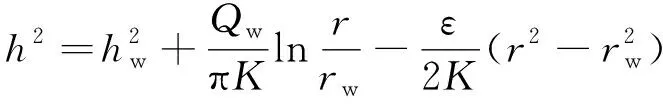
(9)
或将式(6)中Qw代入式(9),得
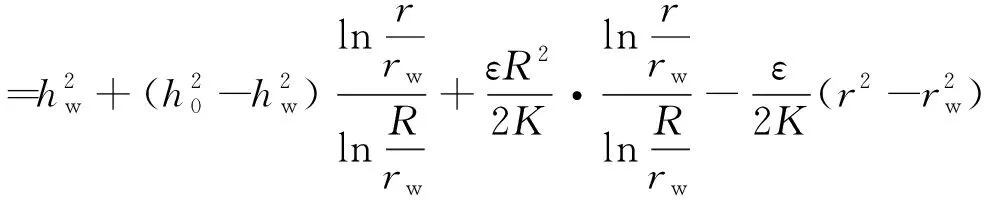
(10)
这就是水位曲线方程。
由式(9),若Qw=0且rw→0,则得未抽水时圆岛天然潜水位的分布:
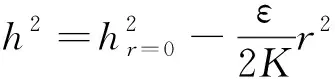
(11)
当r=R时,h=h0,则有
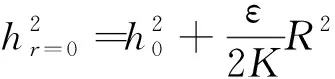
(12)
此即未抽水时,位于圆岛中心处的最高潜水位。
将式(12)代入式(11),得
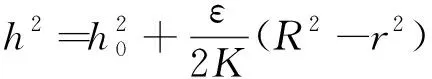
(13)
(2)地下水分水岭
由于
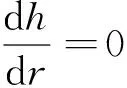
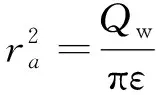
(14)
其物理意义十分明确,抽水井的流量来自于地下水分水岭以内的入渗补给量。
定义抽水条件下地下水的分水岭位置为ra,其相应水位为ha。
由式(8),在Q=0处,r=ra,有
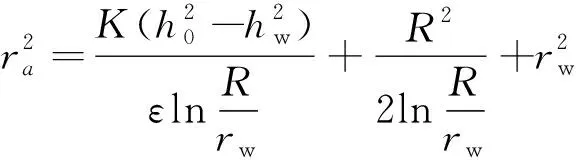
(15)
在r=ra处,h=ha,由式(9)可得ha公式:
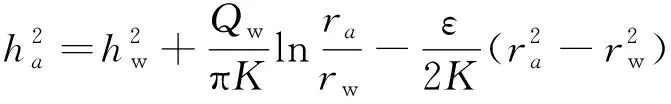
(16)
式(6)的Qw代入式(16)或者直接由式(10)可得由边界水位、含水层参数及入渗强度表示的潜水分水岭的水位:
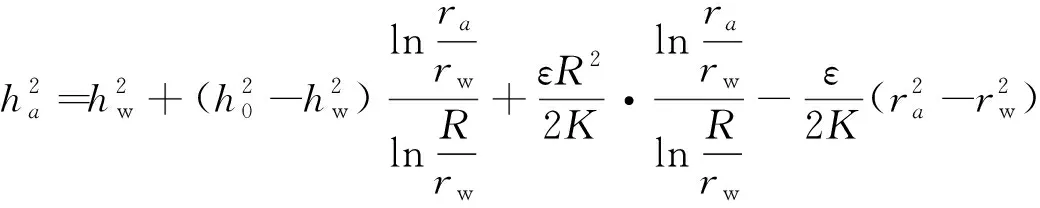
(17)
3 解析方程的基本用途
3.1 求取含水层渗透系数K及入渗强度ε
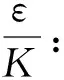
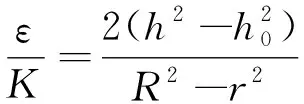
(18)
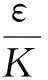
事实上,将式(18)代入式(9)可得
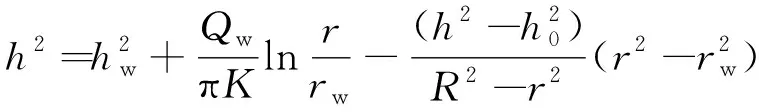
(19)
由此,当r=r1、h=h1时,可以解得
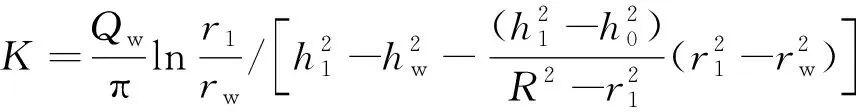
(20)
3.2 计算不同条件下的水位及流量
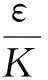
若已知参数K及ε,给定Qw,则可利用式(6)计算hw;反之亦然。
若令Qw=πR2ε,则依式(6)计算的hw,是截取全部入渗补给量的抽水井中的水位。
3.3 有关Dupuit假定及应用新公式注意事项的初步讨论
在建立解析方程的过程中,假设满足Dupuit假定。引入Dupuit假定,对本问题解析研究可以降维(略去z变量)而使有关方程变得简单明了。然而实际上,在某些r断面上是会出现偏离Dupuit假定的,主要在地下水分水岭附近。这一点,Bear(1972年)[4]有过相关的讨论。即使没有入渗补给的原始Dupuit模型,如果潜水含水层厚度与圆岛半径之比较大, 且当抽水井水位降深与潜水含水层厚度之比较大时,在抽水井附近也会出现偏离Dupuit假定。已知非完整抽水井附近的三维流,向外逐渐转变为二维流(忽略z分量),此径距r大约是含水层厚度的1.5倍[3]。借助这一研究成果,估计Dupuit假定(忽略z分量)不满足的地段,可能小于含水层厚度的1.5 倍。上述种种偏离Dupuit假定对解析结果影响的定量分析,还需要进一步研究。
认识到Dupuit假定在某些区段可能会有所偏离,那么在抽水试验求取含水层有关参数时,观测孔的部署要尽量回避这些区段。
4 结论及讨论
(1)对Dupuit圆岛稳定井流模型做了改进, 即考虑垂向入渗补给(蒸发示为其负值)作用,建立了新模型相关的流量方程及水位方程。当所建的新方程中的入渗强度ε取值为零时,其方程蜕变为经典的Dupuit方程。
(2)讨论了新的解析方程的基本用途。新模型可以用于求取含水层渗透系数K、入渗强度ε等参数。
(3)有关Dupuit假设对所建方程的影响做了初步讨论,对抽水试求取水文地质参数的观测孔部署也提出建议。
(4)至于新模型要求入渗是均匀稳定的,在应用中怎么考虑?这个问题是解析模型的一个普遍问题,不仅限于这个新模型。例如,经典的具有入渗的河间地区模型[3],它的入渗也是均匀稳定的。然而在自然界,一般入渗是不均匀,不稳定的,应用中怎么办?至今没有见到讨论。实际上,当今已经广泛使用的数值模拟是可以用来研究此问题的,即做大量的不同尺度和不同参数的组合进行模拟研究,以此可以得出解析方程近似应用的条件。但此项研究是下个课题的任务。
地下水井流问题,这是当今地下水动力学理论和应用最主要的课题之一。从1863年的Dupuit稳定井流模型问世到今天的150多年里,发展了Theis 不稳定井流模型、越流系统井流模型、各类潜水井流模型、二元结构含水系统井流模型等,这么重要的井流问题,尚没见到一个已考虑自然界地下水系统不可或缺的入渗补给条件的。因此,作为初次研究有入渗补给的井流问题,我们是从Dupuit稳定井流模型,而且其入渗是均匀且稳定的简单条件开始。后续还有多个课题有待学者们研究。笔者期待更多创新成果出现。

