黄河三角洲浅层地下水埋深动态与降水的时空响应关系

张晨晨，黄 翀，何 云，刘庆生,李 贺，吴春生,刘高焕

(1.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101；2.中国科学院大学，北京 100049；3.中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室西藏拉萨农田生态系统国家野外科学观测研究站，北京 100101)

受人类活动及气候非线性变化的影响，水文过程的不确定性日益增加，水资源管理面临更大的挑战。黄河三角洲成陆时间短，地下水埋深浅，矿化度高。地下水埋深动态不仅与黄河三角洲土壤盐渍化密切相关，还在很大程度上影响着三角洲湿地生态系统的发育演化[1]。地下水是黄河三角洲区域水循环的重要组成部分，其补给方式主要包括降水和黄河径流补给，海洋潮汐也对地下水有一定影响[2]。近年来，随着黄河入海水量的急剧减少，黄河径流对三角洲地下水补给的作用明显减弱[3]，降水成为影响区域地下水埋深动态的最主要因素[4]。然而，现代黄河尾闾改道频繁，地层岩性复杂，不同时期的沉积物相互重叠，还夹杂着一些不透水的透镜体[5]。在不同空间上，地下水埋深对降水的响应关系十分复杂。深入分析黄河三角洲地下水埋深与降水的关系，不仅有助于理解气候变化条件下河口三角洲地区地下水埋深动态与模式，还可为黄河三角洲退化湿地恢复、土壤盐渍化防治等生态环境治理提供决策依据。

基于时间序列分析的地下水埋深与降水的关系研究是众多学者关注的热点。由于土壤水分、地形、大气环流和人类活动等自然和人为因素的影响，地下水和降水时间序列大多表现为非平稳时间序列，时间和频率尺度变化较大[6-7]。在常用的时间序列分析方法中，频谱分析法适用于动态历时曲线周期成分比较显著的长序列平稳动态数据。与传统的频谱分析不同，小波分析将时间序列分解为时频域，并能分析时间序列中功率的局部变化。由小波变换发展而来的交叉小波变换(Cross Wavelet Transform，XWT)和小波相干(Wavelet Coherence，WTC)可以定量评价两组非平稳时间序列在多尺度周期上的相互关系和时滞特征[6]，在气象、天文等领域得到广泛应用，但是在地下水领域应用较少[8]。降水对地下水埋深的影响具有空间差异性，Chinarro等[9]利用交叉小波变换研究了地下水位和降雨信号间在时频域的相关性，发现地下水和降水在8～80 d的周期分量上具有高度相关性。Yu等[10]结合交叉小波变换和经验正交函数分析研究了2005—2010年台湾屏东平原地下水位变化与降水之间的时空非线性关系，识别了地下水变化的三种时空模式，并进一步确定了不同模式地下水位变化与降水之间的滞后模式。Duvert等[11]发现地下水埋深对高强度降水的响应更为敏感。前人研究大多集中于地下水过程较为单一的地区，针对黄河三角洲地区复杂地下水动态研究关注较少，地下水埋深变化规律及其影响机制尚未得到深入揭示[4, 12]。本研究旨在利用5年的地下水连续观测数据，探究黄河三角洲地下水埋深与降水的时空关系，以期为黄河三角洲地区水循环过程研究及地下水资源管理和生态保护提供参考。

1 研究区概况与数据

1.1 研究区概况

现代黄河三角洲位于山东省东营市境内(图1)，该区域内地貌条件独特，自然资源丰富，社会经济发展迅速。现代黄河三角洲由黄河冲积物淤积而成，主要土壤类型为潮土和滨海盐土[13]，土壤质地以粉砂质为主[5]。区域地势自西南向东北缓慢降低[14]，微地貌类型主要包括缓平坡地、低平地、河漫滩地和黄河泛流主流带高地等[15]。研究区属于温带大陆性季风气候，年均气温为12.3 ℃，年均降水量为532.6 mm，其中70%的降水集中在夏季[16]。由于成陆时间短，地表高程低，区域地下水埋深较浅，矿化度较高。降水是该区域地下水主要补给方式之一。由于同时受河、海、陆交互作用，同时叠加人类活动的影响，使得该地区地下水动态更为复杂[12, 17]。

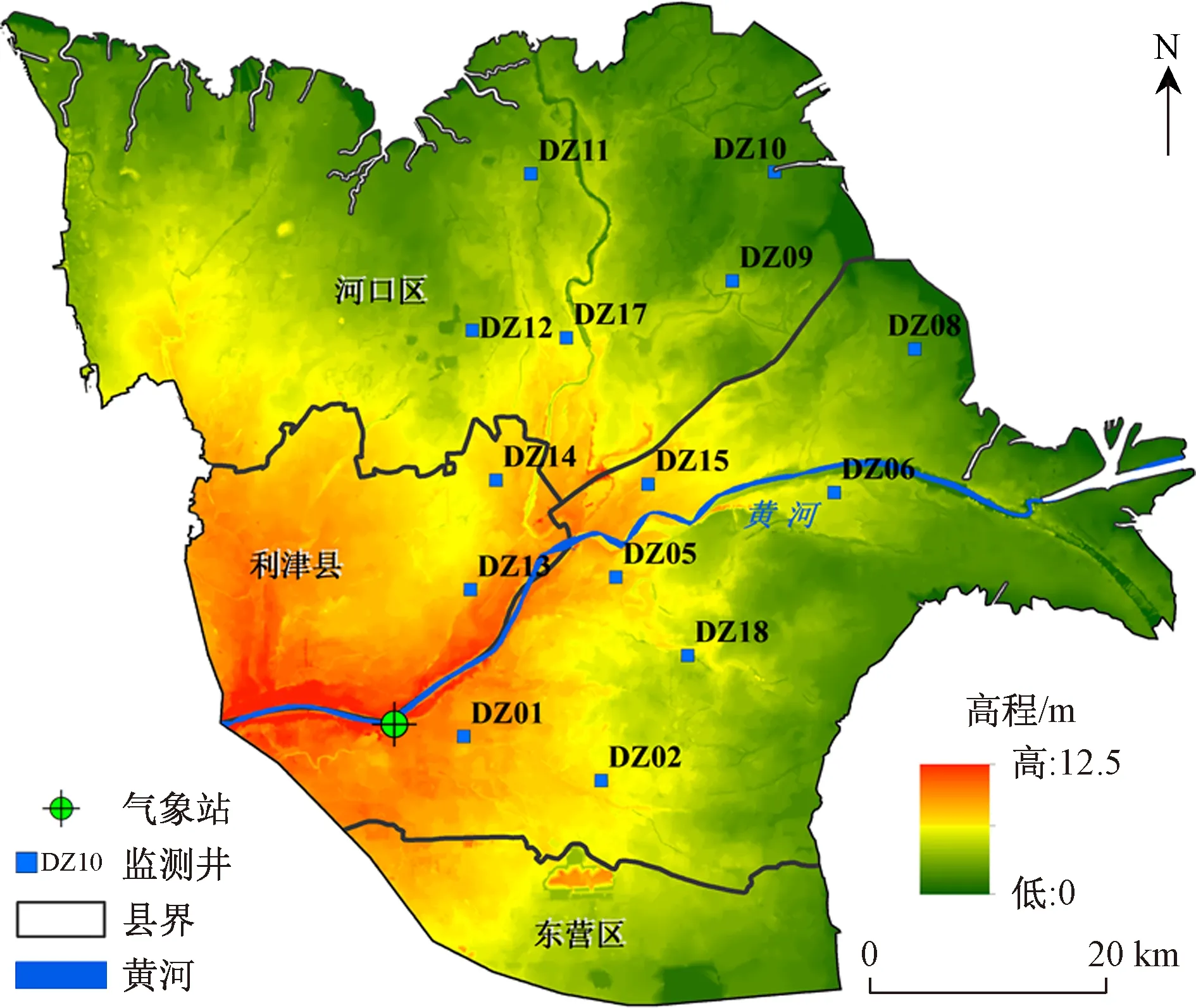
图1 研究区位置及井位分布Fig.1 Location of the study area and the observational wells

1.2 数据及处理

主要研究数据包括地下水埋深数据、降水数据和研究区基础地理数据。为观测黄河三角洲不同空间上地下水动态特征，中国科学院地理科学与资源研究所在不同地貌单元上布设了14口地下水监测井(图1)，监测时段为2006年5月2日—2010年3月27日，观测时间间隔为5 d。降水量数据采用研究区内的垦利气象站(站号：54744)日值数据，数据来自于中国气象数据网(http://data.cma.cn/)。为了与地下水观测数据时间和频率对应，取5 d累计值进行分析。在进行地下水埋深和降水的相关性分析时，所有数据都采用z-score方法进行标准化处理。土地利用数据来自于第二次全国土地调查数据，根据研究区情况进行适当类别合并(图2a)，微地貌类型(图2b)和土壤质地(图2c)数据来自文献[15]。

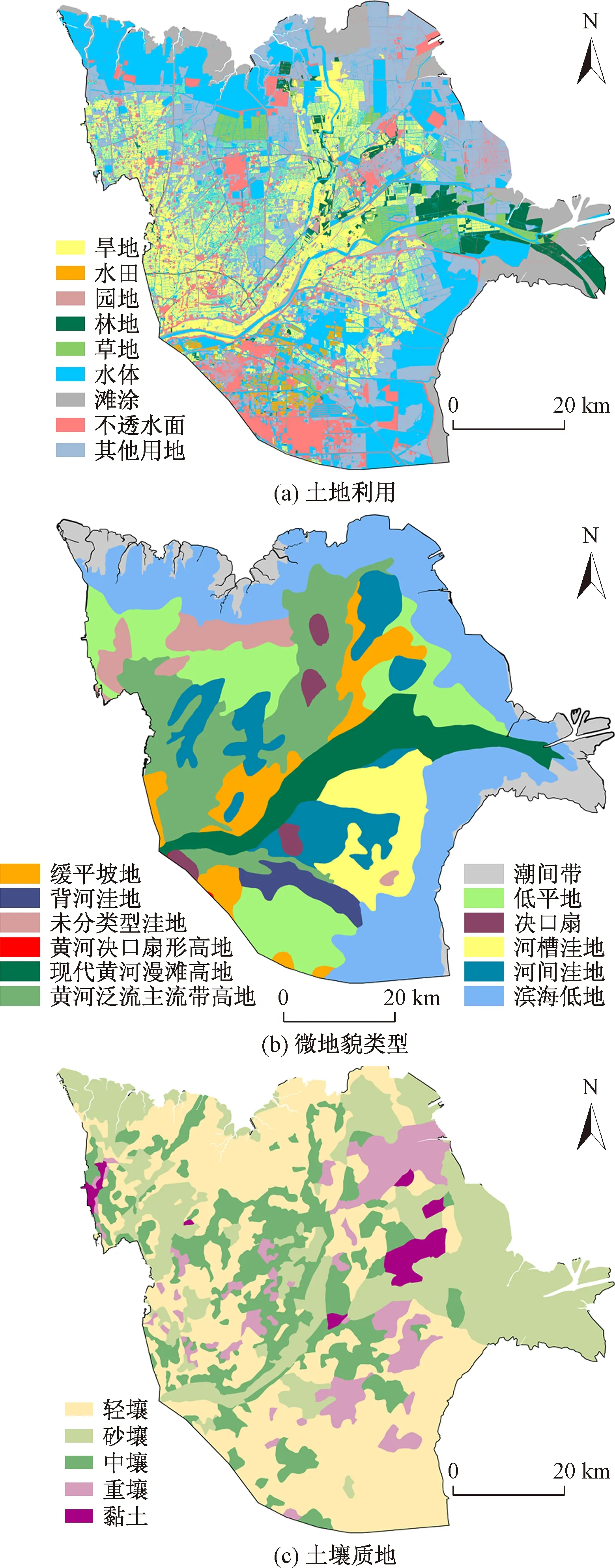
图2 土地利用、微地貌类型和土壤质地图Fig.2 Land use, micro-geomorphic types and soil texture

2 研究方法

为研究黄河三角洲地下水埋深对降水的时空响应关系，首先利用Kendall’s秩相关及反距离权重空间插值识别地下水埋深对降水响应的主要空间模式。基于交叉小波变换和小波相干方法，揭示不同模式地下水埋深对降水在时频域上的具体响应过程。结合土地利用、微地貌类型及土壤质地资料，基于地理探测器方法，探究影响地下水埋深对降水响应关系的驱动因子。

2.1 Kendall’s秩相关

Kendall’s秩相关是衡量两个时间序列相似程度的非参数统计方法，不需要样本遵从一定的分布，而且不受少量极端值和缺失值的干扰，因此在水文及气象分析研究中得到广泛应用[18]。本文利用Kendall’s秩相关系数划分地下水埋深对降水的空间响应模式。对于两个时间序列Xn={x1,x2,…,xn}和Yn={y1,y2,…,yn}，相关性计算公式为[19]：

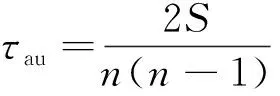
(1)

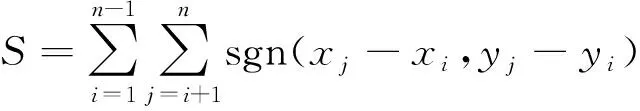
(2)

式中：τau——两时间序列相关系数；

S——统计变量。

τau的取值范围为[-1，1]，当τau取值为正时，表示两个时间序列拥有一致的等级相关性；反之，两个时间序列拥有相反的等级相关性。

2.2 交叉小波变换

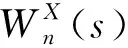
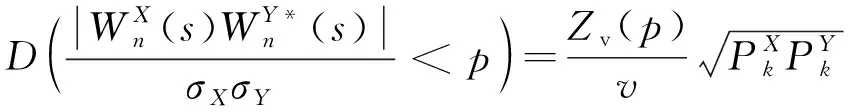
(3)

式中：*——复共轭；

σX——Xn的标准差；

σY——Yn的标准差；

Zv(p)——概率p的置信度水平。显著性水平α=0.05时，Zv(p)=3.999。

当式(3)的左端超过置信限，则认为通过了95%置信度下的红噪声标准谱的检验，Xn和Yn相关性显著。

2.3 小波相干

为了分析多个时间尺度上不同分量的时间变化，采用小波相干方法识别时频域上时间序列Xn和Yn的协方差强度，小波相干定义[6]为：

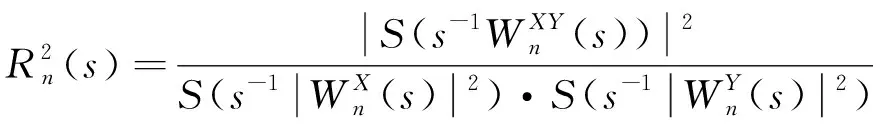
(4)

S(W)=Sscale(Stime(Wn(s)))

(5)

Sscale——沿着小波伸缩尺度轴平滑；

Stime——沿着小波时间平移轴平滑。

Morlet小波的平滑器定义[20]为：

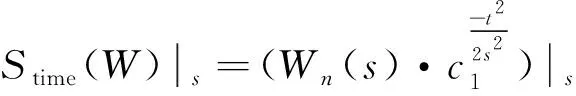
(6)

Sscale(W)|s=(Wn(s)·c2∏(0.6s))|n

(7)

式中：c1、c2——标准化常数；

∏——矩形函数；

0.6——根据经验确定的与Morlet小波波长的解相关的尺度参数。

短路保护是指在电路发生不经过负载或导线电阻几乎忽略不计等故障时，瞬间产生极大的电流提供切断电源，防止设备损坏而造成事故的保护方式。在正常供电的电路中，电流的流经路径形成一个闭合回路，如果在电流通过的电路中，两导线相触碰或者被另一小电阻物质短接引起短路现象。如果短路保护出现故障，低压配电系统的正常运行将会受到阻碍，人们正常生活和工作也将受到一定地影响。

2.4 地理探测器

地理探测器(Geographical Detector)是一组揭示因变量空间分异性及其背后驱动因素的统计学方法。其核心思想的假设为：如果某个自变量X对因变量Y有显著影响，则两变量的空间分布应该具有相似性[21]。地理探测器不仅可以探测驱动因子对因变量的单独影响，还可以评估两因子共同作用对因变量的解释力。相比于主成分分析和多元线性回归等较常规的统计学方法，地理探测器具有定量分析各驱动因子交互作用的优势[22]。本文利用地理探测器中的因子探测器分别检测土地利用、微地貌类型和土壤质地对地下水埋深与降水响应关系的影响，用交互作用探测器检测两驱动因子交互对地下水埋深与降水响应关系的作用。

因子探测器用q值度量某驱动因子X对因变量Y的空间分异的解释力，q值的表达式[21]为：

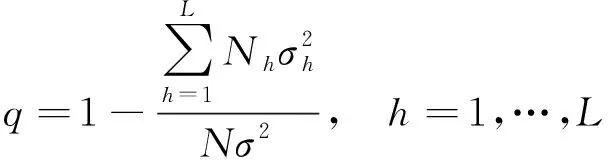
(8)

式中：L——因变量Y或驱动因子X的分层；

Nh——层h的单元数；

N——全区的单元数；

σ2——全区Y值的方差。

q的值域为[0，1]，表示驱动因子X解释了(100×q)%的因变量Y，q值越大，自变量X对因变量Y的解释力越强。

交互作用探测器用于评估驱动因子X1和X2共同作用时对因变量Y的解释力，根据q(X1)、q(X2)和q(X1∩X2)之间的关系，判断驱动因子X1和X2之间是独立作用还是交互作用，以及其交互表现为协同作用还是抑制作用(表1)。

表1 两因子对因变量交互作用的类型

3 结果与分析

3.1 浅层地下水埋深与降水量时间序列相关性分析

浅层地下水埋深和降水量的Kendall’s秩相关系数τau的范围为-0.45～-0.01。采用反距离权重插值方法对τau进行空间插值，得到τau的空间分布图(图3)，反映了地下水埋深与降水量相关性的空间特征。可以看出，地下水埋深对降水量的响应在空间上存在差异。基于τau值，将研究区地下水埋深和降水量时间序列之间的关系划分为3种空间模式：模式1强负相关(-0.45～-0.30)，随降水量增加，地下水埋深显著降低；模式2负相关(-0.30～-0.15)，降水量增加会引起地下水埋深一定程度的降低；模式3弱负相关(-0.15～-0.01)，降水量的变化对地下水埋深影响微弱(图3)。

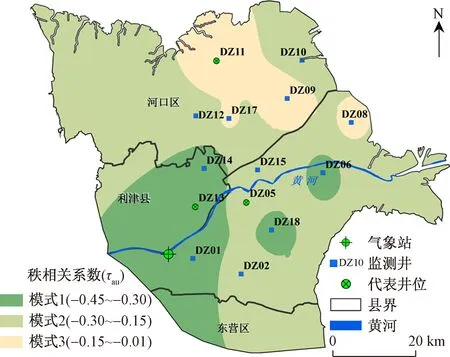
图3 地下水埋深与降水的空间模式Fig.3 Spatial patterns between groundwater depth and precipitation

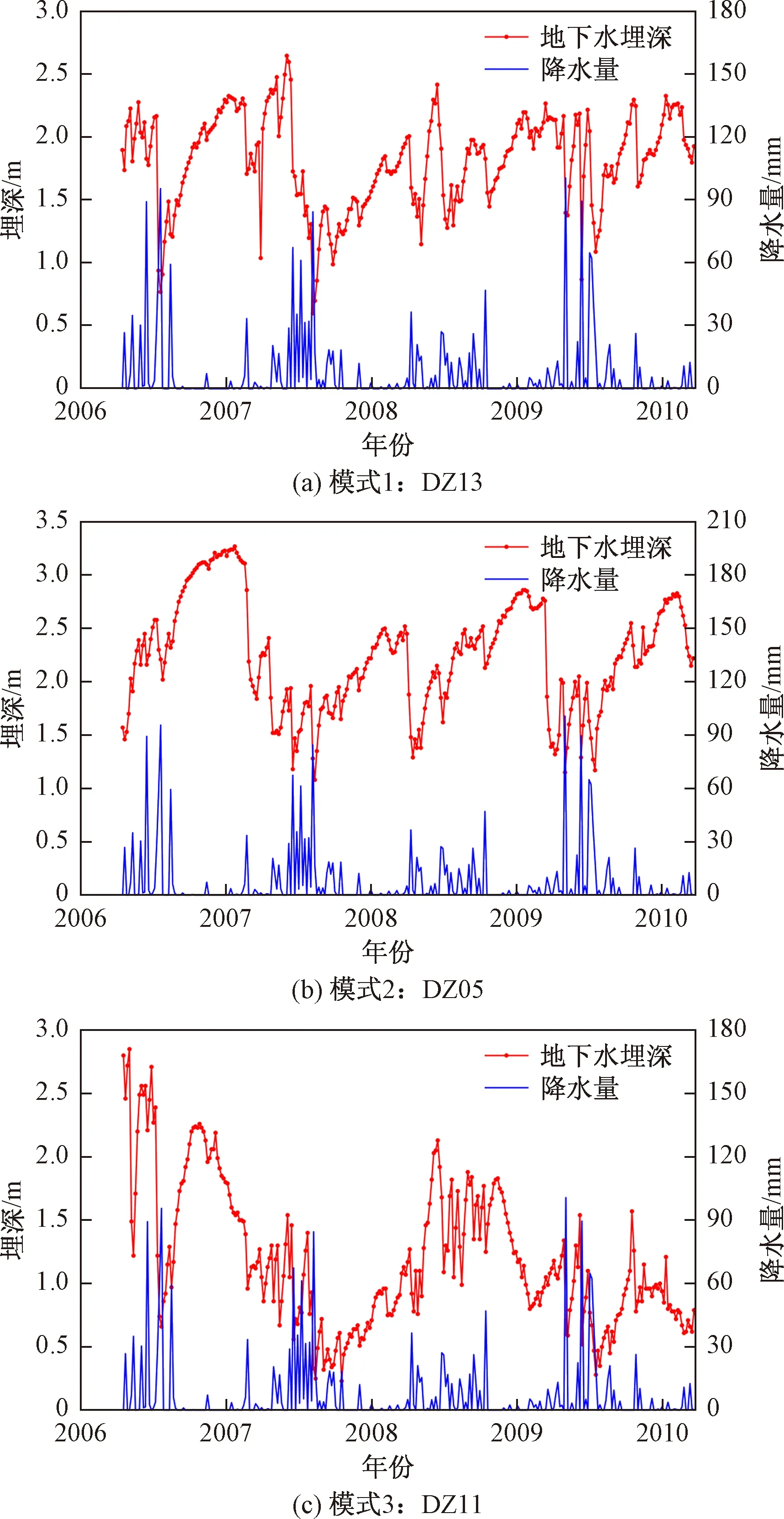
图4 三个模式的地下水埋深和降水时间序列Fig.4 Time series of groundwater depth and precipitation for the three patterns during 2006 to 2010

每个空间模式选取位于该模式主要微地貌类型内的一口井作为该模式的代表井位进行分析。图4为三个模式的地下水埋深和降水时间序列统计图。可以看出，三种模式的地下水埋深年内变化特征基本一致。一年中，地下水埋深基本呈先上升、快速下降，然后缓慢上升的变化趋势，埋深最低值一般出现在7月、8月，最高值则出现在1月、2月。DZ13(模式1)、DZ05(模式2)和DZ11(模式3)的地下水平均埋深分别为1.81，2.24，1.19 m(表2)。DZ13和DZ05位于内陆，地下水埋深相对较深，而位于海滨的DZ11埋深较浅。总体来看，2006—2010年，模式1和模式2的埋深处于动态平衡的状态，而模式3埋深整体呈现降低的趋势。

3.2 地下水埋深-降水在时、频域上的响应特征

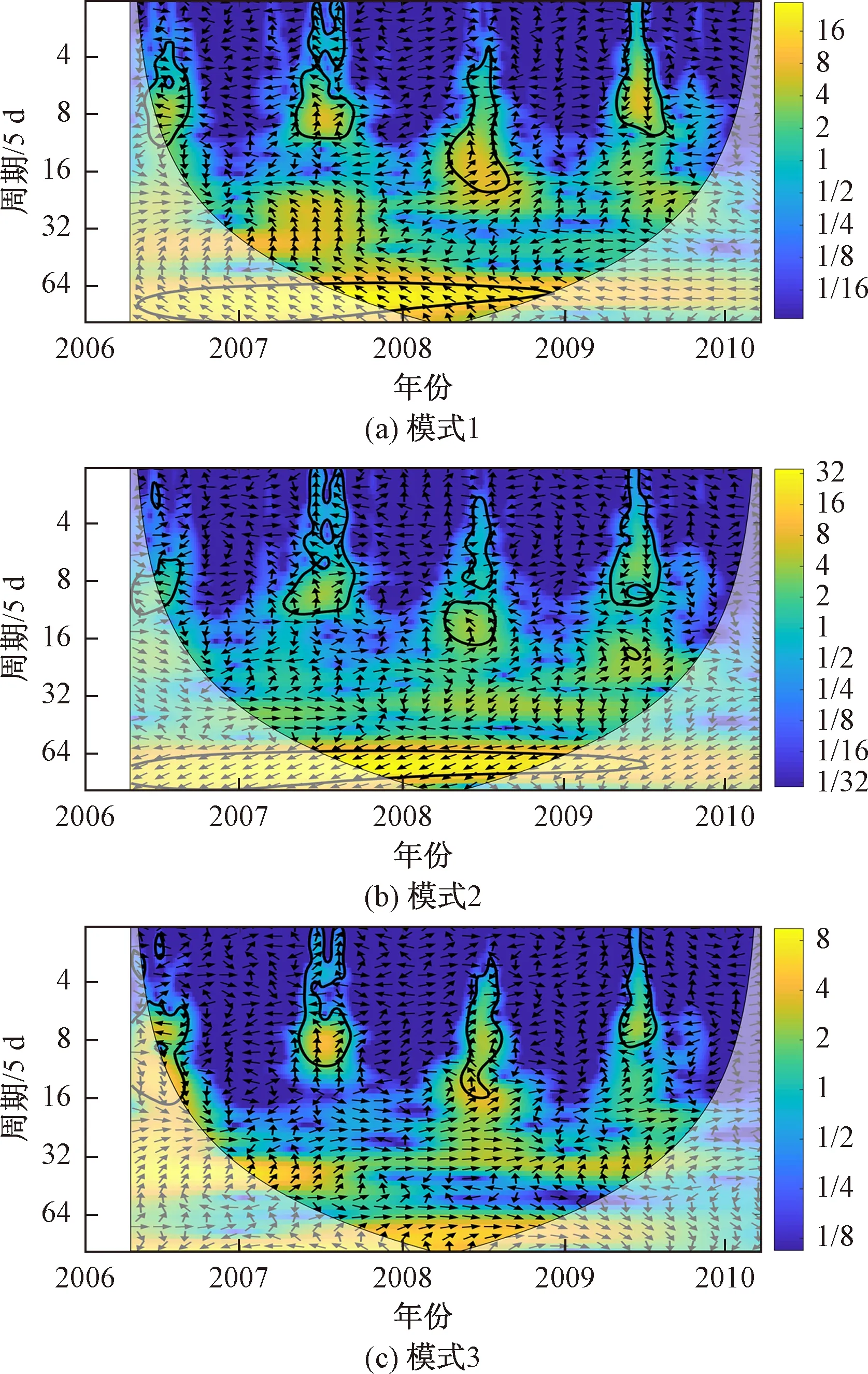
→正相干 ←逆相干 ↑滞后1/4周期 ↓滞后3/4周期图5 三个空间模式的地下水埋深与降水的交叉小波变换结果Fig.5 The cross-wavelet transform (XWT) between precipitation and groundwater depth for three spatial patterns

对三种空间模式的代表井位分别进行交叉小波变换(图5)，以进一步分析地下水埋深和降水在时频域上的共振周期、显著时段和相位关系等。图5中，交叉小波变换结果图例的蓝色与黄色分别表示能量密度的谷值和峰值，黑色粗实线圈闭的值通过了95%置信水平的红噪声检验，黑色细实线下方锥形区域为小波影响锥(Cone Of Influence，COI)区域，是交叉小波变换数据边缘效应影响较大的区域[6]。箭头矢量的方向代表相对相位关系，指向右侧表示两个时间序列相位一致(正相位)，即地下水埋深和降水同时变化或者滞后降水一个周期变化；箭头指向左侧表示两个时间序列相位相反，相差π相位(逆相位)，说明地下水埋深相对于降水滞后1/2个周期，两者变化过程相反；箭头垂直向上(下)表示两个时间序列相差π/2相位，箭头垂直向上表示地下水埋深相对于降水滞后1/4个周期，箭头垂直向下表示地下水埋深相对于降水滞后3/4个周期。

在模式1(图5a)和模式2(图5b)中，地下水埋深和降水均具有非常明显的320～480 d(64×5～96×5)的主共振周期，显著时段分别为2006年5月—2008年12月和2006年5月—2009年5月。模式3(图5 c)没有超过95%置信度的长周期，且小波功率明显小于模式1和模式2。此外，随着频率的增加，三个模式都具有明显的间歇性周期，虽然周期范围有差异，但显著时段相近。例如，在2006年，模式1具有20～60 d(4×5～12×5)的共振周期，模式2具有30～60 d(6×5～12×5)的共振周期，模式3具有30～85 d(6×5～17×5)的共振周期。局部共振周期的显著时段也是降水量显著增加的时段，强降水通过包气带渗入迅速补给地下水，随之地下水埋深在该时段内发生突变，在中高频率下呈现较强的季节性。相比于雨季，旱季降水次数和降水量大大减少，地下水埋深对降水的响应不如雨季显著。图5中的箭头矢量所示，每个模式高频域相位角随时间变化很大，不同模式相差也很大，而低频域相位角方向在时间上基本稳定。

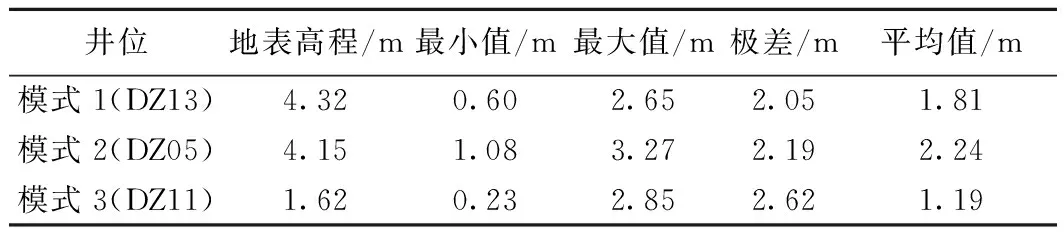
表2 监测井位地表高程及地下水埋深统计

基于交叉小波变换的结果，计算平均相位角(表3)，得到地下水埋深对降水响应的滞后时间。模式1、模式2、模式3的平均相位角分别为3.068 7 rad、2.519 4 rad、0.610 9 rad，地下水埋深相对于降水的平均滞后时间分别为178.36 d、146.43 d和35.51 d。从模式1到模式3，平均相位角逐渐减小，说明地下水埋深变化相对于降水量的响应时间也在逐步缩短。

结合图5和表3，模式1和模式2交叉相位的标准差偏差均未能改变相位符号，说明相位关系相对稳定，而模式3的标准差大于平均相位，相位符号发生改变，说明该模式下地下水埋深与降水的关系不稳定。模式3分布于滨海低地，地下水埋深较浅，地下水和降水交替变换频繁，使得该模式下不具有显著的连续长周期。

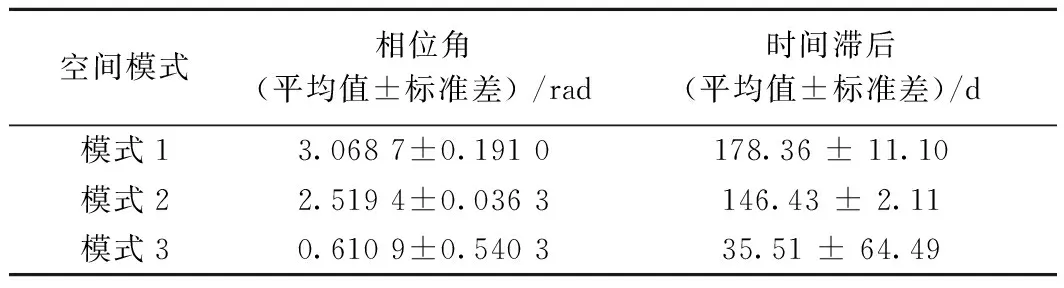
表3 三个空间模式的平均相位角和时间滞后统计

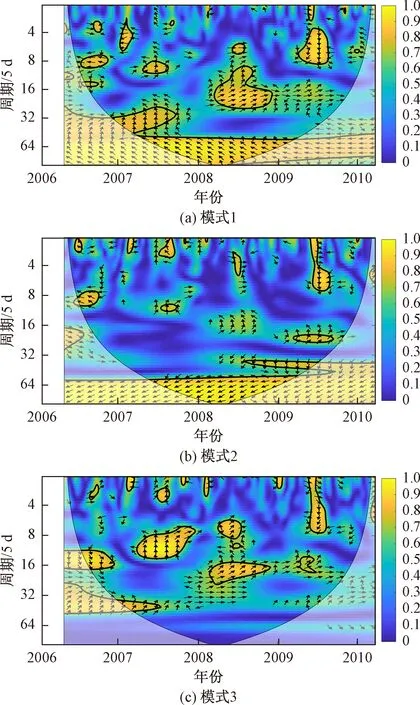
→正相位 ←逆相位 ↑滞后1/4周期 ↓滞后3/4周期图6 三个空间模式的地下水埋深与降水的小波相干结果Fig.6 Wavelet coherence (WTC) between precipitation and groundwater depth for the three spatial patterns

交叉小波变换(XWT)用来检测两个时间序列共振能量较高的区域，但是即使共振能量很低，两序列也可能具有显著的相关性。因此，本研究利用小波相干分析(WTC)进一步探究降水与地下水埋深的相关性。WTC结果中右侧的色阶柱表示两个时间序列的相干性(0～1)，值越大，两个时间序列的相干性越强，反之则越弱。由WTC的结果(图6)可以看出，在320～480 d(64×5～96×5)的低频范围内，模式1和模式2的地下水埋深和降水量在全时段内都存在非常显著的相关关系(图6a、6b)，但模式3(图6 c)没有和模式1、模式2一样的长周期相干性。除了交叉小波变换分析中提到的间歇性共振周期，WTC发现了更多的局部相干性。例如，模式1(图6a)中，2006年的35～50 d(7×5～10×5)和2007年20～35 d(4×5～7×5)，模式2(图6b)中，2006年的35～55 d(7×5～11×5)和85～155 d(17×5～31×5)；模式3(图6 c)中，2009年的0～45 d(0×5～9×5)和75～120 d(15×5～24×5)等，地下水埋深和降水在这些范围上具有显著的强相干性。

3.3 地下水埋深对降水响应关系的驱动因子

地理探测器通过探测因变量与驱动因子之间空间分布格局的相似性，度量驱动因子对因变量的解释度，即q值。本研究中，因变量为地下水埋深与降水间的秩相关关系，驱动因子为土地利用类型、微地貌类型和土壤质地。因子探测器探测结果为：三种驱动因子中，微地貌类型对降水-地下水埋深关系的解释度最大，为0.280 7，土地利用为0.244 1，土壤质地为0.163 8。这说明微地貌类型是影响降水-地下水埋深响应关系的最主要因子，土地利用类型其次，土壤质地类型重要性稍低。由交互作用探测器探测结果(表4)可知，地下水埋深对降水的响应是多种因素共同作用的结果，不存在相互独立起作用的因子，不同因子之间的叠加可极大增加单因子对地下水埋深-降水响应关系的解释力，均表现为非线性增强关系，其中，土地利用和微地貌类型的协同增强作用最大，为0.749 0。

表4 交互作用探测器探测结果

4 讨论

小波相干检测出三种空间模式中存在许多相干性很大的间歇性共振周期，这些局部周期体现了强降水对地下水埋深在短时间内快速变化的明显影响，这一现象在以往研究[10, 23]中也有发现。Qi等[23]利用快速傅里叶变换方法分别重构了地下水位和降水信号，表明地下水动态对强降水的响应非常敏感；Yu等[10]通过对地下水和降水信号进行不同频率下的逆连续小波变换(Inverse CWT)，同样发现地下水位变化的高频周期与强降水高度相关。与高频周期中频繁变化的相位角相比，低频周期的相位角较为稳定。在地下水埋深波动中，低频信号是土壤质地、有机质、地下水埋深、平均入渗通量等的函数[24]，一般比强降水等高频信号保存的更好，所以持续降水在地下水补给过程中起着更重要的作用。

土壤质地、微地貌类型及土地利用等因子主要通过影响降水入渗过程进而影响地下水埋深变化。本研究中，微地貌类型对降水-地下水埋深响应关系的解释度最大。模式1的代表井位DZ13所处的微地貌类型为河漫滩高地，模式2的代表井位DZ05附近的微地貌类型为河槽洼地，模式3的代表井位DZ11周围的微地貌类型为滨海低地。不同类型微地貌是影响水文连通性的重要因素，与降雨的再分配过程密切相关[25]。总体来说，黄河三角洲地区地势平坦，稍有起伏的微地貌增加了地表粗糙程度，凹陷的地表在降水过程中具有更强的“捕水”能力[26]，水分入渗效率得以提高。土地利用作为人类活动对生态系统影响的综合反映，对地下水埋深-降水响应关系有着不可忽视的影响。本文中地下水埋深与降水秩相关系数绝对值较大的区域与耕地分布具有较高的一致性，这可能是因为耕作能够增加土壤孔隙度，加之栽培作物对降雨的截留功能和废弃秸秆对降水的滞蓄，更加利于降水入渗[27]。所以这种土地利用下，地下水埋深与降水之间的相关性较高。地下水埋深与降水相关系数绝对值较小的区域对应的土地利用多为盐碱地和裸地等其他用地、滩涂和不透水面，这些土地利用类型降水的入渗难度较大，更容易形成超渗产流，下渗补给地下水较少，地下水埋深与降水之间的相关性较弱。对于土壤质地，以往研究大都表明其与降水入渗密切相关[28-29]，土壤质地通过影响土粒的表面能和土壤孔隙度，进而对降雨入渗能力产生影响[30]。但在本研究中，土壤质地对地下水埋深-降水响应关系的解释度最低。这可能是由于该研究区轻壤分布广泛，土壤质地的空间差异性较小，加之人类活动强烈，从而削弱了土壤质地对地下水埋深-降水响应关系的影响。

需要指出的是，黄河三角洲地处河口海岸带地区，区域地下水埋深动态是河-海-陆复杂交互作用的结果。区域地下水埋深除了主要受降水影响外，也会受到海洋潮汐、黄河径流等过程的影响。但潮汐作用和黄河径流对于区域浅层地下水的影响都只限于一定的范围[31]。因此，本文在探讨地下水埋深对降水的响应时，没有深入分析潮汐和黄河径流的影响。由于黄河三角洲水文循环过程的复杂性，局部地区河-海-陆多因子交互作用的耦合程度和机制仍需进一步研究。

5 结论

结合Kendall’s秩相关、交叉小波变换和小波相干方法，分析了黄河三角洲浅层地下水埋深对降水不同的时空响应模式，利用地理探测器探究影响地下水埋深对降水响应的驱动因子，主要结论如下：

(1)地下水埋深与降水量时间序列呈负相关关系，Kendall’s秩相关系数τau的范围为 -0.45～-0.01，空间差异性明显，其关系根据τau值可以分为三种空间模式：模式1强负相关(-0.45～-0.30)、模式2负相关(-0.30～-0.15)和模式3弱负相关(-0.15～-0.01)。

(2)从模式1到模式3，地下水埋深对降水的响应延迟时间越来越短，分别为178.36 d、146.43 d和35.51 d，模式1和模式2地下水埋深和降水量的相位关系相对稳定，而模式3的标准差大于平均相位，地下水埋深与降水的关系不稳定。在所有模式中，都存在很多局部共振周期，说明地下水埋深动态对强降水的响应非常敏感。

(3)土地利用、微地貌类型和土壤质地对地下水埋深和降水的关系都有显著的影响。从相对重要性来说，微地貌类型贡献最大，其次是土地利用类型和土壤质地。驱动因子之间都表现出协同增强作用，土地利用和微地貌类型的协同增强作用最显著。