40 t轴重列车作用下铁路简支梁桥的梁轨纵向相互作用
陈浩瑞 刘吉元 杜振华 石龙
(1.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081;2.中铁第四勘察设计院集团有限公司,武汉 430063)
我国以大秦铁路和晋中南铁路为代表的重载铁路主要开行轴重为25~30 t的货运列车,随着货运需求的增加,研究建设40 t轴重重载铁路具有重要意义[1]。列车荷载的提高会影响桥梁、轨道、路基等结构的安全性与平顺性,对桥上无缝线路纵向力产生重要影响。因此,有必要针对40 t 轴重列车作用下的铁路简支梁桥梁轨纵向相互作用规律开展研究。
殷明旻等[2]基于国外重载铁路的设计参数,利用简化的均布荷载计算了40 t轴重重载铁路桥上无缝线路纵向力,并给出了桥墩线刚度建议值。戴公连等[3]研究了30 t轴重重载铁路简支梁桥上无缝线路纵向力和墩台水平力分布规律,分析了跨数、布置方式和工况组合方式对梁轨相互作用的影响,提出了30 t 轴重重载铁路线刚度建议值。颉明军等[4]对内蒙古巴准铁路哈拉沟特大桥进行有限元分析,研究了重载列车作用下无缝线路纵向力的分布规律,得到了万吨大轴重列车牵引制动工况下桥墩台承受的最大纵向力。闫斌等[5]建立了考虑桩土作用、桥墩塑性变形、滑动支座阻力的梁轨相互作用模型,提出了30 t 轴重重载铁路梁轨系统的地震响应规律,分析了温度、列车制动和地震耦合作用下该系统的受力特征。于哲[6]建立非等跨简支T 梁与轨道一体化模型,通过加载30 t 轴重移动荷载列研究了无缝线路纵向力的分布规律以及温度作用、制动作用、地震作用对该梁轨系统的影响。根据研究现状可知,国内学者主要侧重外部作用变化和桥梁参数变化对无缝线路纵向力的影响,但关于纵向位移阻力曲线变化对重载铁路无缝线路纵向力的影响研究较少。基于此,本文结合几内亚Simandou 重载铁路建立有限元模型,分析40 t 轴重重载铁路无缝线路纵向力对纵向位移阻力曲线的适应性。
1 计算模型

图1 线桥一体化杆系模型
采用有限元软件建立线桥一体化杆系模型(图1)。梁体线单元与代表2股钢轨的钢轨线单元在竖向使用间隔0.65 m 的刚臂弹簧单元连接,在纵向采用间隔0.65 m 的非线性弹簧单元连接。线路纵向位移-阻力曲线通过参数形式赋值于纵向非线性弹簧单元内。梁端下缘刚臂线单元连接固定支座与活动支座,支座节点竖向自由度、横向自由度全部固定。固定支座与墩顶节点采用刚臂弹簧单元连接,活动支座与墩顶节点采用极柔的线性弹簧单元连接。墩台采用“墩顶节点+纵向线性弹簧+全约束的墩底节点”模式进行模拟,墩台顶线刚度值赋予在相应的纵向线性弹簧单元中。图1中h=0表示2个节点在同一水平面上,位置重合,但相对独立。
2 计算参数
2.1 桥梁参数
桥梁参数参考几内亚Simandou 铁路Kaba 河桥跨区段的相关设计参数,建立单线10 跨24 m 的双工字钢主梁钢-混结合梁桥。该线路是为开发世界级铁矿——几内亚西芒杜铁矿而设计的配套货物运输铁路。为了确定墩顶线刚度,在同一跨度下,采用60,80,100,150,175,200,250,300,400,500,600,800,1 000,1 500,3 000 kN/cm 共15种刚度进行计算,桥台刚度采用1 500 kN/cm。梁体伸缩作用下的温差为±20 ℃。
2.2 荷载参数
采用澳大利亚BHP 矿石车进行加载,相应单节构造简图如图2所示。

图2 澳大利亚BHP矿石车单节构造简图(单位:m)
2.3 轨道参数
钢轨采用CHN60轨。对于有砟轨道,线路纵向位移-阻力曲线主要采用TB 10015—2012《铁路无缝线路设计规范》[7]中规定的有砟轨道Ⅲ型混凝土轨枕纵向位移-阻力曲线,见图3。
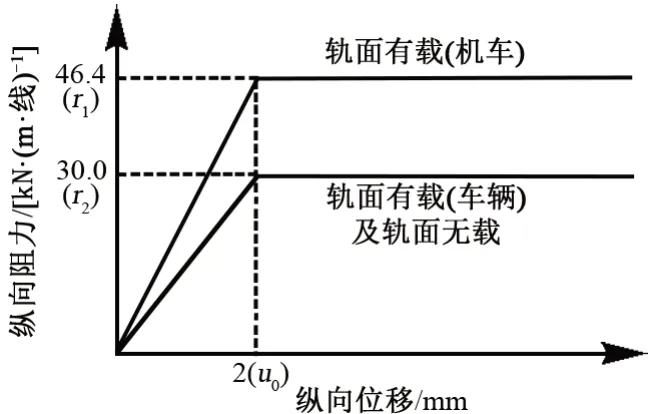
图3 有砟轨道线路纵向位移-阻力曲线
为了研究线路纵向阻力变化对重载铁路无缝线路纵向力的影响,结合图3 构建不同的纵向位移阻力曲线,变化数值分别见表1 和表2。其中,轨面有载纵向阻力为轨面有载(机车)对应的纵向阻力。
2.4 检算限值
有砟轨道钢轨附加拉、压应力限值分别为81,61 MPa,梁轨快速位移差限值为4 mm。

表1 随纵向阻力变化的线路阻力取值

表2 随屈服位移变化的线路阻力取值
3 计算结果
采用TB 10015—2012中的纵向位移-阻力曲线计算得到40 t轴重重载列车作用下钢轨制动附加应力最大值及制动+温度的组合附加应力最大值随墩顶线刚度变化的曲线,见图4。可知,在制动工况和组合工况下,钢轨附加拉、压应力随墩顶线刚度的变化规律大致相同,附加压应力略大于附加拉应力。附加压应力限值比附加拉应力限值小,而实际情况相反,说明钢轨附加压应力起控制作用,因此本文只对制动工况和组合工况下的钢轨附加压应力进行分析,下文的压应力统一取绝对值。
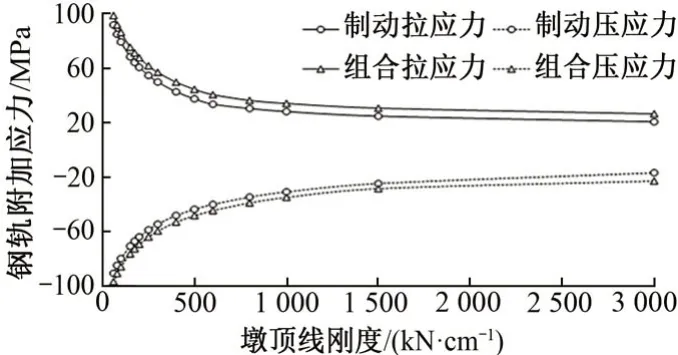
图4 40 t轴重重载铁路钢轨附加应力最大值曲线
3.1 钢轨附加应力
有砟轨道单线简支梁40 t轴重重载列车钢轨制动附加压应力最大值曲线见图5。由图5(a)可知,当墩顶线刚度不超过400 kN/cm 时,钢轨制动附加压应力最大值随纵向阻力的增大而增大;当墩顶线刚度超过400 kN/cm 时,钢轨制动附加压应力最大值先迅速减小,随后缓慢增加。由图5(b)可知,当墩顶线刚度不超过1 000 kN/cm时,钢轨制动附加压应力最大值随屈服位移的增大而减小;当墩顶线刚度超过1 000 kN/cm时,钢轨制动附加压应力最大值先减小后增大。

图5 钢轨制动附加压应力最大值曲线
3.2 梁轨快速位移差
根据表1 和表2 计算40 t 轴重重载列车在有砟轨道单线简支梁上产生的梁轨快速位移差最大值,见图6。可知,同一刚度下,梁轨快速位移差最大值随纵向阻力的增大而减小;梁轨快速位移差最大值随屈服位移的增大而增大,呈现明显的线性关系。

图6 梁轨快速位移差最大值曲线
3.3 墩顶线刚度限值讨论
采用不同纵向阻力和屈服位移计算得到了24 m跨度40 t轴重重载铁路有砟轨道单线钢混简支梁的墩顶线刚度限值,分别见表3 和表4。可知:①40 t 轴重重载铁路简支梁墩顶线刚度为537 kN/cm,与文献[2]的研究结果(540 kN/cm)大致相同。②40 t 轴重重载铁路对墩顶线刚度要求较高,仅单一改变线路纵向阻力或屈服位移均不能很好地解决重载铁路墩顶线刚度限值偏大的问题,可以采用在跨中专门设置制动墩或变多跨简支梁为连续梁等方法,从整体上优化桥梁-轨道纵向受力。

表3 不同纵向阻力下的墩顶线刚度限值

表4 不同屈服位移下的墩顶线刚度限值
4 结论
1)当墩顶线刚度较小时,同一刚度下钢轨制动附加压应力最大值随纵向阻力的增大而增大,随屈服位移的增大而减小。
2)同一刚度下,梁轨快速位移差最大值随纵向阻力的增大而减小,随屈服位移的增大而增大。
3)同一刚度下,纵向阻力变化对桥上无缝线路纵向力的影响大于屈服位移变化对纵向力的影响。
——提竿钓法的浮标

