例谈寻找解题切入点的策略

王凤君

[摘  要] 解题是数学学习中的一项重要活动，解题能力的提升离不开有效的解题训练，自然更少不了一些必要的解题策略. 教师需从以下几个方面着手，引导学生找寻解题切入点，发展解题能力：挖掘隐含条件，剖析结构特征，运用特殊化策略，采用数形结合以及利用差异分析法.

[关键词] 解题;隐含条件;解题路径;切入点;差异分析

数学的学习离不开对解题的探索，如何通过必要训练去提高解题能力，应是广大数学教师和学生不断思考与探索的课题. 笔者在平常的教学中发现，不少学生在解题的时候存在以下问题：有些题目似曾相识，即使冥思苦想却依然找寻不到解题入口，当别人稍加提点却又豁然开朗. 事实上，“老虎吃天，无处下爪”是学生在解题中的常见现象，究其根本在于学生尚未找寻到解决问题的突破口，当适当点拨时又会恍然大悟.所以，解题教学中需强化、引导学生去选择一个容易攻克的切入点，由点及面，让问题的本质逐步自然展现. 那么，如何找寻解题的切入点呢？下面笔者通过对多个案例的探究，谈谈具体的解决策略.

隐含条件：获得解题路径的关键

隐含条件，望文生义就是隐藏在数学问题中的一些含而不露的条件，它可以隐于图形之中，也可藏于概念之中，还可匿于已知条件的相互联系之中. 因此，在解题中学生需善于将这些隐含于题目中的“金针”挖掘出来，从而获得解题的关键性突破，使问题迎刃而解.

例1：已知直线m被两条平行线l1：x-y+1=0和l2：x-y+3=0所截线段长度为2■，那么直线m的倾斜角可能是①15°;②30°;③45°;④60°;⑤75°. 以上符合要求的序号有________. （请写出所有正确答案的序号）

分析：通过观察，不难得出本题中已知条件有①l1，l2为两条平行直线;②直线m被l1，l2所截线段长度为2■. 而以上两个条件对于问题中需求直线m的倾斜角是远远不够的，那么下一步自然就需要深入题目挖掘隐含条件. 首先，据条件“l1，l2为两条平行直线”，可以探求出两直线间的距离为■;接着，再次观察不难发现：直线m被l1，l2所截线段长度为l1，l2之间距离的两倍;然后，借助作草图可以发现，直线m与直线l1的夹角为30°，而直线l1的倾斜角为45°，则可很快得出直线m的倾斜角为30°+45°=75°或45°-30°=15°，故本题答案为①⑤.

设计说明：让学生通过计算l1，l2之间的距离，并结合线m被l1，l2所截线段长度为2■，感知隐含条件的挖掘过程，得出隐含条件“直线m与直线l1的夹角为30°”，突破思维的难点，从而快速求解.

结构特征：构成解题路径的基石

一般数学题都具有明显的结构特征，而其中的结构特征往往直指解决问题的切入口. 这就需要在解题过程中，仔细观察题目的外部特征，深入分析题目的深层结构，在剖析问题的结构特征中抓住问题的切入点，实现条件向结论的转化.

例2：已知f（x）=■，试求出f（1）+f（2）+f■+f（3）+f■+f（4）+f■的值.

分析：本题可以首先计算f（1），f（2），f■，f（3），f■，f（4），f■的值，然后再求出f（1）+f（2）+f■+f（3）+f■+f（4）+f■的值，然而过程的烦琐是可想而知的. 此时，不妨去观察式子f（1）+f（2）+f■+f（3）+f■+f（4）+f■的特征，很快可以发现f（2）和f■，f（3）和f■，f（4）和f■中每一对自变量乘积都等于1，遮挡规律的“外衣”被迅速剥离，从而自然想到考虑这三对函数值的特征. 不少学生可以思考到去计算f（2）+f■，从而引申到f（x）+f■，則有f（x）+f■=■+■=■+■=1，所以f（1）+f（2）+f■+f（3）+f■+f（4）+f■=■+1+1+1=■.

设计说明：学生在解题时，需将着眼点置于对题目目标结构特征的分析和联想上，有针对性地找寻解题的入口，从而快速找到解题的有效策略.

特殊化策略：获得解题入口的捷径

人们认识客观事物的普遍规律就是从特殊到一般的思路. 因此，在探究一些一般性问题的时候，我们可以通过研究它的某些特殊情形，为问题的探求提供帮助，从而找寻到问题的解决入口. 而正是这种特殊化策略的灵活运用，才能将认识过程中以退为进的思想方法体现得淋漓尽致.

例3：如图1，已知长方形ABCD中，有AB=2，BC=1，且E为DC的中点，动点F在线段EC上（不与E，C重合）. 现沿AF折起△AFD，使得平面ABD⊥平面ABC，在平面ABD内过点D作DK⊥AB于K点.设AK=t，那么t的取值范围为________.

分析：本题若以一般方法着手解决，过程烦琐且难度较大. 若从特殊化策略入手，也就是从两个极端位置进行思考，则可简化解题过程. 当动点F移动到DC的中点时，可以得出t=1. 当动点F移动到C点时，有CB⊥AB，CB⊥DK，所以CB⊥平面ADB，即CB⊥BD. 因为CD=2，BC=1，所以BD=■. 又因为AD=1，AB=2，所以AD⊥BD，则t=■，由此可得t的取值范围为■，1.

设计说明：本题通过引导学生思考动点F的两个特殊位置“DC的中点和C点处”，从而快速找寻到解决本题的入口，给出特殊化策略解题的范例，让学生感悟复杂问题和一般问题的解题方法.

数形结合：寻求解题入口的法宝之一

数形结合解题的重点是数与形的相互表征，实现数与形的相互转化.在数形结合解题的过程中，找寻数与形的转化途径从而寻找解题突破口不仅是一个重点，也是一个难点. 因此，在解题教学中，教师可以通过富有探究性的题目，引领学生从问题本身进行探索性活动，在解决问题的过程中，将抽象的数学语言与直观的图形相沟通，实现抽象与具体的转化和渗透，大跨度地迁移自身已有的思维方式，从而找寻到解决问题的突破口.

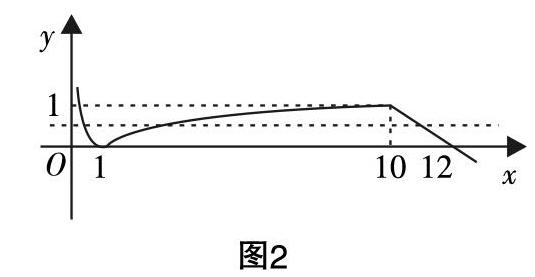
例4：已知函数f（x）=lgx，010.若a≠b≠c，且f（a）=f（b）=f（c），则abc的取值范围为（  ）

A（5，6） B. （1，10）

C. （20，24）？摇？摇？摇？摇？摇？摇 D. （10，12）

分析：易得函数f（x）为分段函数，可以通过作草图来演绎图像的变换，由此简化解题过程. 观察图2可知，若要f（a）=f（b）=f（c），可以设a

设计说明：通过本题的典型性来凸显数形结合思想方法的优势，让学生在解决问题的过程中，培养学生思维的发散性和想象力，在解题完毕还可以进一步进行总结与提升，在回顾和概括中提升思想方法的应用能力.

差异分析法：寻求解题入口的又一利器

在解题中，我们会发现一些题目的条件与结论之间无论在形式或结构上，还是在图形或文字间都存在着一定的差异性，我们将它们之间的差异称为“目标差”. 成功解题的关键就是从找寻目标差入手，通过一个方案的设计来不断缩小这里的目标差，直到目标差消除，从而在找寻、分析、消除目标差的过程中快速形成解题方案，这种解决问题的方法就是差异分析法. 该方法可以帮助学生快速找寻到解题入口，成为解决复杂数学题的利器.

例5：已知tan2θ=-2■，■<θ<π，试求■.

分析：首先，从角的差异着手，目标中除θ以外，还有■和θ+■，分析题设，只能找寻到2θ这一个，而事实上它们都可以转化为θ;其次，從三角函数名称的差异着手，目标中仅有“弦”，而题设之中仅有“切”，事实上它们也可以相互转化.从而，成功突破本题的关键在于缩小并消除角与三角函数名称的目标差.

解：原式=■=■=■. ？摇据tan2θ=■= -2■，可解得tanθ=-■或tanθ=■. 因为■<θ<π，tanθ=-■，所以原式=■=3+2■.

设计说明：本题巧借差异分析法，从找出差异开始搭建解题通道，并不断变换思维的视角，关注到角与三角函数名称的目标差，快速联结解题的思维路线，在消除目标差的过程中完善解题路径.

总之，解题教学的价值并非在于解题的数量，而是需借助解题活动来提升学生解决问题的策略，这才是解题教学的价值取向. 因此，我们在精选例题训练时，需站在学生的角度，精选具有典型性和价值性的例题，并以思维为主线，共同展示找寻解题突破口的全过程，让学生在感受和体验中落实每个例题固有的“生长”功能，从而实现解题教学的意义和价值. 只有持之以恒，才能真正意义上解决学生面对难题时“习得无助”的问题.