“双合”课堂下学习任务单的教学实践

叶学琴

[摘  要] “双合”课堂是借鉴前瞻教育理念，通过对传统课堂的研究和实践反思，建立高效的教学模式. 它是构建数学小组合作、学教合一的“双合”课堂组织方式，形成学生的学、教师的教和学生的习“三位一体”的新课堂结构. 在“双合”课堂中，学习任务单给出明确的学习任务，引导学生完成课堂授课内容. 文章通过“三角函数的诱导公式”学习单的六个环节，进行一些教学实践和思考，以期达到数学学科素养的培养.

[关键词] “双合”课堂;学习单;教學实践

《普通高中数学课程标准（2017年版）》指出：既要重视教，又要重视学，促进学生学会学习.[1] 教师在教学过程中，不是自己一味地“填鸭式”授课，而是将重心放在促进学生的互动学习上，包括师生互动与生生互动，努力探究有助于学生学习的多样化教学模式. 教师不局限于讲授与练习，而是引导学生通过问题引领，进行自主学习，再通过合作探究、应用拓展、反思升华等环节. 教师要擅长根据不同的教学内容和学习任务采取不一样的教学模式，再利用反馈评价，整合并优化教学，抓住重要的授课与学习环节，提高课堂效率、增强实际效果.

“双合”课堂

它采取的教学模式是“小组合作、学教合一”，是传统课堂与导学课堂的优势合成，目的是实现课堂教学的有效性和高效性. “双”是师生双方教学相长，生生互教互学，达成多维收获的共赢局面，是教学方式;“合”意指师生合作、生生配合，是教学理念.

“双合”课堂采用的是“三三制”的教学模式，即一部分时间用于学生自主和学生互动，完成练习和小组交流;一部分时间用于展示，由各组对本组存在的问题的讨论结果进行报告;一部分时间用于教师点评、归纳、总结和提升. 各班级采用小组合作的方式，即每个班分成几个小组，每个小组有5～6位学生. 小组有组长和学科组长. 小组统一行动，统一交流，统一评价.[2]

在“双合”课堂我们主要通过“学习任务单”实施教与学，“学习任务单”实际上就是教师为了落实核心素养预设的学习任务. 它是自主学习与合作探究的根本，是实现以学助教的依据. 利用“学习任务单”引导学生从整体上把握课程，教师可以大胆地、适当地“放手”，先于教之前就进入学，让学生养成独立思考与合作探究的习惯. 学生有了明确的学习任务，就可以积累发现和提出问题、分析和解决问题的经验，实现学生数学学科核心素养的形成和发展.[3]

“任务单”学习

它是以学情为依据、为达成学习目标而设计的学习活动的载体，使学生学习目标明确，激发学生的学习兴趣，培养学生合作精神、探究能力和学习能力.

学习单分为六个环节：问题引领——自主学习——合作探究——应用拓展——反思升华——反馈评价. 下面以“三角函数的诱导公式”为例，抛砖引玉.

1. 问题引领

“问题引领”是充分发挥教师的主导作用，让学生围绕教师设计的问题自主探索、研究而达到解决问题的一种教学方式，通过学生亲身的探究活动不断获得新知识、新思维. 问题设计要切合学生的实际水平，对不同层次的学生要求要有梯度. 问题设计主要有以下几方面内容：一是通过已有的知识或方法引申出新知识，学会类比学习;二是针对知识细节或易错点提出问题;三是对概念、公式、定理的关键要素提出问题;四是对应用提出问题;五是让学生进行总结、归纳等.

例如，针对“三角函数的诱导公式”的“问题引领”的设计：

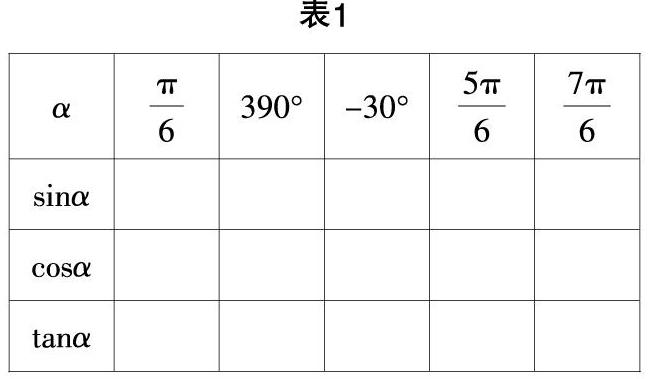
问题1：回顾前面已经学习的理论知识，我们已经学习了任意角的三角函数的定义，学习了三角函数线，还有同角三角函数关系，但是我们还有一个关键问题没有解决，那就是：我们如何来求任意角的三角函数值呢？你能填好下面的表吗？（表1）

问题2：对于任意角α，α与-α，α与π-α，α与π+α，各对角中，终边有怎样的对称关系？

问题3：利用单位圆对称性和三角函数的定义如何发现、推导诱导公式.

思考：预习是培养学生自学能力的重要环节. 有些教师在布置预习作业时，只是要求学生把课本提前看一看，却没有给出明确要求. 很明显，这是一种没有成效、流于形式的预习，这样的预习既浪费时间，又收效极差. “问题是最好的老师”，要想达成高效率的预习效果，就要学会“掘地三尺”，学会问“为什么”. 那么有效的预习应该如何实施呢？这就要求教师在认真钻研教材、分析本班学情的基础上，合理设计“问题引领”，引领学生有计划地进行自主学习.

“一池死水，风平浪静，投去一石，涟漪阵阵，可谓一石击起千层浪.”“问题引领”可能只是课堂情境的创设，或者只是课堂引入的一种铺垫，起到抛砖引玉的作用. 对于设置的问题，难易程度要适中，可以有一定的创造性与挑战性，但要求的目标不能太高. 设计的问题要让大部分学生能自己解决，对于一些较难的问题可以留到课堂上一起讨论交流. “学习单”在上课前一天发放，让学生先完成“问题引领”. 在课前，教师要及时了解学生完成“问题引领”的情况，关注学生未能解决的问题，对于学习有困难的学生加以辅导.

2. 自主学习

促进学生主动学，根据预习内容，创设情境，服务于一堂课的主要内容，为接下来的合作探究打下基础. 自主学习能力的培养要循序渐进，持之以恒. 先从简单做起，如让学生课前阅读教材，粗略了解教学内容;进而是让学生能处理一些简单的应用问题，然后再加大难度，让学生能对概念进行辨析，能对公式、定理进行证明;最后是达到归纳整理或者拓展应用的能力. 自主学习首先是学生要独立完成，然后才在小组里进行探讨合作，或者向教师请教，也要学会通过查阅资料帮助解决问题.

例如，在“三角函数的诱导公式”学习任务单的实施中是这样创设情境的，从而让学生达到自主学习的目的.

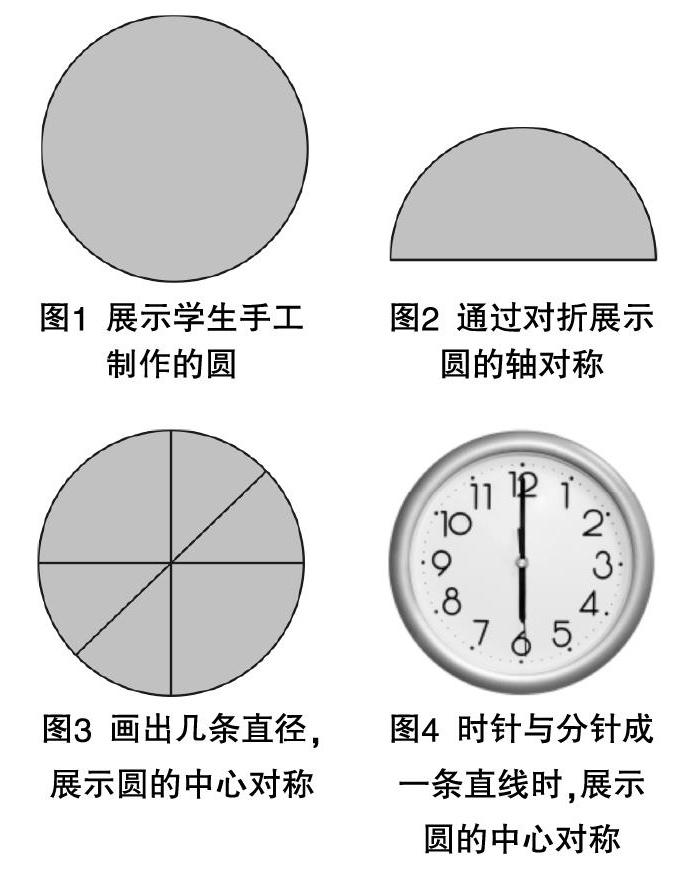
教师：著名的希腊数学家毕达哥拉斯说过“一切立体图形中最美的是球，一切平面图形最美的是圆”. 我们在定义三角函数时已经领会过圆的美. 我们的同学在课前已经准备了圆的道具，请组长出示（有用卡纸做的圆，还有废旧的钟），那么也请组长来展示一下圆的对称性.

预设情境：

学生1：用卡纸做的圆沿着任一条直径对折，直观展现圆的轴对称.

学生2：用挂钟的时针和分针，直观展现圆的中心对称.

思考：爱因斯坦说过“兴趣是学生最好的老师”. 为了培养学生的自主学习能力，需要激发学生对数学的兴趣，有了兴趣就会产生探索新知识的欲望. 因此，在“双合”课堂上，教师应充分发挥自身的主导作用，指导学生自主学习. 教师还要善于设疑，燃起学生思维的火花，进而激发学生的创造性，也给予学生更多参与课堂互动的机会，提升学生的课堂参与度. 各组学生利用道具，演示“问题引领”中的结果. 在“三角函数的诱导公式”的学习中，通过学生自主学习圆的对称美，让数学文化渗透于心. 又如，在学习立体几何时，对一些空间立体感不强、空间想象能力较差的学生，教师可以布置学生自己动手制作一些简单的几何模型，提升学生的想象能力. 通过实践操作、实物展示，让新课程理念凸显于课堂上. 同时，也培养了学生直观想象、数学抽象的数学素养.

3. 合作探究

将重难点知识设计成探究模式，由小组合作共同探究，推动学生参与学习活动. 合作探究首先要做好小组组合，有不同形式，可以是小组里有不同层次的学生，也可以是同等程度的学生组成一组，也可以经常打破组合，但必须是在自主学习的基础上进行合作探究. 探究的内容包括自主学习时各自的问题，或者是课堂上的一道题，或者是合作出题，甚至是学生们课外的问题，等等.

例1：求值sin570°.

设计意图：复习并利用“诱导公式一”，得到sin210°，引出新问题.

探究1：请同学们先用卡纸做的圆或钟大胆探究210°与哪个锐角有关系？请四组同学由组长选送一个代表上台展示探究结果.

预设探究结果：①30°角绕着圆心逆时针旋转半圈就可以得到210°;②210°角与30°角的终边成一条直线;③210°角与30°角的正、余弦线的长度分别相等，方向相反;④210°角、30°角的终边与单位圆的交点关于原点对称.

多媒体：教师利用几何画板直观展示;组长派代表展示道具，看谁的道具更具实用性.

注：分别用几何画板、手工制作展示210°角与30°角的终边关系.

探究2：如何求sin210°，cos210°，tan210°的值？

预设探究结果1：利用三角函数线大小和方向得到答案.

设计意图：选择合适的道具，复习并应用三角函数线解决问题.

预设探究结果2：30°，210°的终边与单位圆的交点分别是P（x，y），P′（-x，-y），它们关于原点对称. 利用三角函数的定义得到答案.

设计意图：通过圆的对称性、三角函数的定义解决问题，渗透对称变换思想和数形结合思想. 注重现代信息技术与传统教學的融合，体现教学方式的多样性.

探究3：sin（180°+α）与sinα的关系.

教师：将30°改为α，210°改为180°+α. 板书：“诱导公式二”的推导过程.

多媒体：教师通过几何画板动态演示α由30°变成任意角，验证结论，学生通过道具操作.

注：分别用几何画板与手工制作展示α与180°+α的终边关系.

教师板书：诱导公式二（用弧度制表示）：sin（π+α）=-sinα;cos（π+α）=-cosα;tan（π+α）=tanα.

设计意图：通过几何画板将特殊角过渡到任意角，从而得到“诱导公式二”. 体现特殊到一般的数学思想.

探究4：分组探究sin-■和sin■的值.

预设探究结果：①-■，■的终边与单位圆的交点分别是P（x，y），P′（x，-y），关于x轴对称，利用三角函数的定义有sin-■=-sin■，cos-■=cos■;②■，■的终边与单位圆的交点分别是P（x，y），P′（x，-y），关于y轴对称，利用三角函数的定义有sin■=sin■，cos■= -cos■.

设计意图：通过类比的方法自主探究.

探究5：■改为任意角α呢？

多媒体：教师用几何画板动态演示，任意角α与-α的终边与单位圆的交点关于x轴对称，即P（x，y）？圮P（x，-y）;π-α与α的终边与单位圆的交点关于y轴对称，即P（x，y）？圮P（-x，y）？摇？摇

设计意图：结合几何画板的动态演示，直观形象地展示轴对称点的坐标变换过程，从而导出诱导公式. 注重数学课程与现代信息技术的适度融合，实现传统教学难以达到的效果.

注：用几何画板分别展示α与-α、α与π-α的终边关系.

合作学习：下面第一、二小组同学完成-α与α的三角函数值的关系;第三、四小组同学完成π-α与α的三角函数值的关系. 大家一起比赛，看谁先得出结果？得出结果的同学求值sin570°.

学生板书：诱导公式三：sin（-α）= -sinα，cos（-α）=cosα，tan（-α）=-tanα;

诱导公式四：sin（π-α）=sinα，cos（π-α）=-cosα，tan（π-α）=-tanα.

探究6：“诱导公式四”能否利用前面几个公式推导出来？

设计意图：师生共同得出π-α=π+（-α），体现划归转化的思想. 另外，一些重要的结论往往都是“看”出来的，会“看”其实就是直观想象素养，诱导公式的推导提供了培养直观想象素养的平台.

思考：《普通高中数学课程标准（2017年版）》指出：把握数学本质，启发思考，改进教学. 教师创设合适的教学情境，启发学生思考与探究，引导学生慢慢地获取数学知识. 合作探究要面向全体学生，合理安排探究内容. 对于探究的问题，要有一定的高度和深度，但又要在学生的最近发展区内，适合大部分学生的认知水平. 另外，探究的问题可以具备一定的开放性，学生不必按部就班，允许他们有自己的想法，只要不偏离主题，他们可以按照自己的想法进行探索. 通过数学课堂展开“双合课堂”教学模式，结合教师、学生对“双合课堂”教学模式的合作学习的认识，改变传统的教与学的方式，变讲堂为学堂，不断巩固学生的主体地位，使学生逐步会发问、会求知、会合作，提高自主学习、独立思考、合作探究能力，最终把握数学内容的本质. 同时，也培养了学生逻辑推理、数学运算的数学素养.