基于听觉特性的舰船辐射噪声信号仿真

周 烨 温 玮 范赵鹏 杨日杰 李沛宗

(1 海军航空大学战勤学院 烟台 264001)

(2 中国人民解放军91001 部队 北京 100089)

0 引言

舰艇辐射噪声仿真对水声装备研制以及水声对抗技术发展都具有重要意义。关于舰艇辐射噪声仿真，国内外学者已经进行了许多研究[1-2]。以往的模型针对舰艇辐射噪声基本上是将辐射噪声分为线谱、连续谱和调制谱分别建模。针对线谱和调制谱建模往往以单频信号进行叠加，在幅度和相位上进行随机处理，这样仿真的信号只能代表其特征频率，且在听觉感受上与实际信号相差甚远[3]。近年来，有不少文献讨论了将音色参量用以进行目标识别，并取得了不错的成果[4-6]。在信号仿真领域，一般不对音色参数进行考虑，导致仿真信号在听觉感受上与实际信号差别很大[7]。噪声信号频谱中各类线谱组幅值大小及其连续谱分量是影响噪声音色的重要部分，依据实测信号调整仿真信号线谱幅值以及连续谱分量可以在一定程度上改善听觉感受。但是由于实测噪声信号中各类线谱繁杂，在某些特征线谱之外还存在随机线谱，有时特征线谱也会发生偏移，这些往往与舰艇的航行状态或者环境扰动有关系，在建立仿真模型时一般不对其进行考虑。因此直接通过实测信号线谱幅值构建仿真信号线谱幅值所得到的结果往往并不理想。本文通过实测数据构建特征滤波器，并基于实测数据的音色参量来构建线谱族的特征幅值参量，通过对比整体实测信号的听觉特性来搜索符合特征样本音色的线谱族幅值参量，在一定程度上改善了仿真信号的听觉特征，而又不失一般性，得到了符合工程应用的结果。

1 线谱模拟

舰艇辐射噪声线谱成分主要与其动力系统、推进器有关系[1]。在这其中，由舰艇推进器运转产生的线谱信号与螺旋桨转速有一定关系，其幅值与频率随转速变化，拥有一系列谐波分量，可以表示为

式(1)中，n表示谐波号数，m为叶片数，s为转速，主要分布于100 Hz以下的低频带。另一部分主要由机械噪声组成，包括连续运转的工作部件产生的周期分量，主要有机械不平衡导致的噪声、往复不平衡导致的噪声以及齿轮噪声，柴油机工作时往复机活塞导致的拍击噪声、电动机推动时产生的电磁力脉动噪声。这类噪声频谱结构比较复杂多变，分布于1000 Hz以下的低频带。对于线谱信号仿真，其信号模型可以表示为

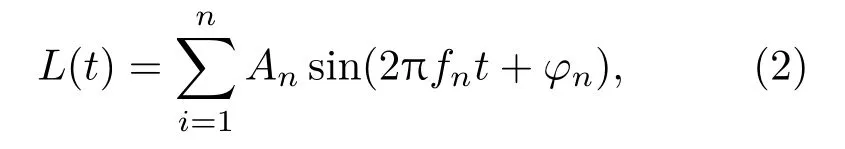
其中，an为相应分量幅值，fn表示由叶片和机械两部分噪声频率分量组成，φn表示随机相位。

2 连续谱模拟

连续谱分量是由连续的频率分量组成，因此可以在时域上用一组平稳随机信号来进行模拟，将高斯白噪声信号通过满足噪声频谱特性要求频率响应的有限脉冲响应(Finite impulse response,FIR)滤波器即可得到连续谱分量[8]。

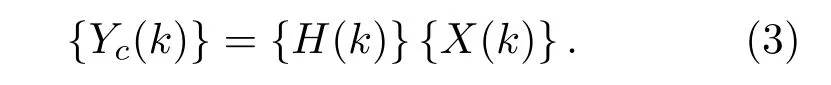
最后，将{Yc(k)}进行反傅里叶变换，得到时域序列{Yc(m)}，{Yc(m)}即为具有高斯振幅分布，谱级曲线满足要求的连续谱时域序列。

为了更好地模拟舰船辐射噪声连续谱特性本文采用兼顾频谱参数和听觉感受的方法，利用采集到的不同航行状态下的舰艇目标噪声谱，进行平滑平均处理后针对其特征谱峰频率、谱级设计特定频响的滤波器，通过宽带噪声来模拟连续谱噪声[9]。

首先对获取的某航船目标在中速运动的辐射噪声谱进行连续谱提取并进行平滑平均处理，采用的是某商船目标的辐射噪声信号，采样率为22 kHz，其连续谱信号如图1所示，为了方便提取滤波器设计所用参数，对实测信号进行平滑处理，如图2所示。

提取上述连续谱的谱峰频率f0以及相应的谱级SL0，文献[9]中按照人耳的听觉特性采用了倍频程取样法，取得了不错的成果。本文在处理取样问题借鉴了相关手段，在[1,f0)和(f0,fs/2]两个区间同时按照倍频程取样，按照相应的样本构建特定频率响应滤波器，如图3所示。

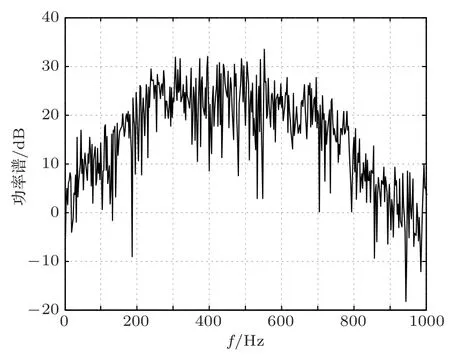
图1 提取连续谱噪声Fig.1 Extracting continuous spectrum noise

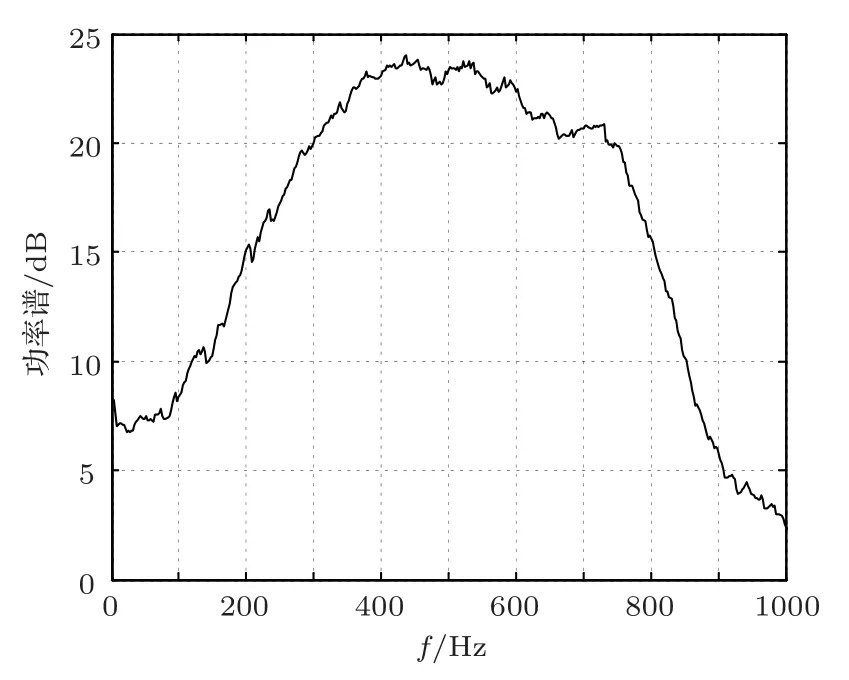
图2 平滑处理Fig.2 Smoothing

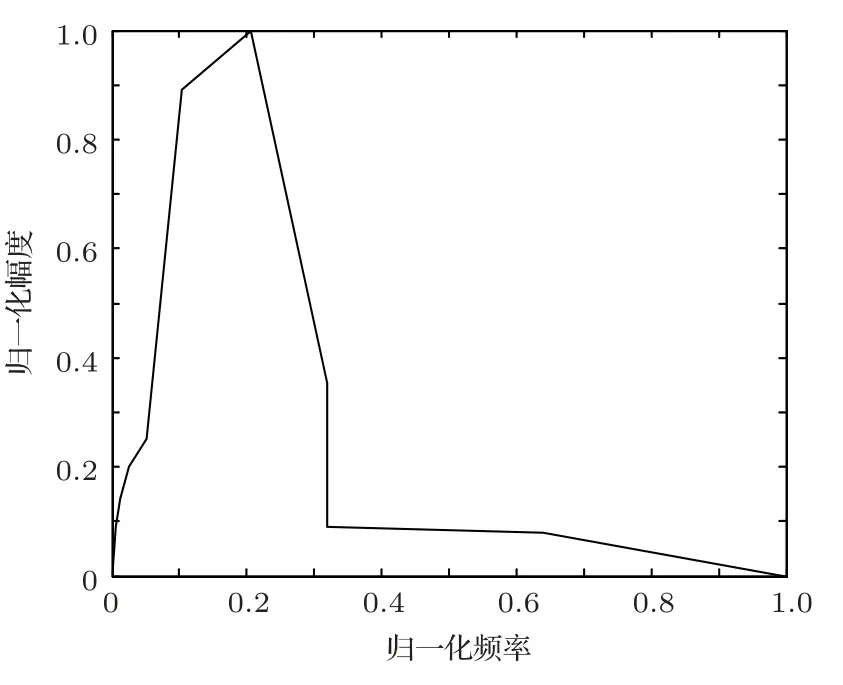
图3 特定滤波器幅频响应Fig.3 Specific filter amplitude-frequency response

利用响应的滤波器对高斯白噪声进行滤波，就可以得到相应的连续谱噪声。此方法可以在保持目标特征谱峰位置和幅度的同时更加符合人耳的听觉感受，较好地仿真了噪声信号谱。

3 调制谱模拟

在构建调制谱时，其模型主要表示为[6]

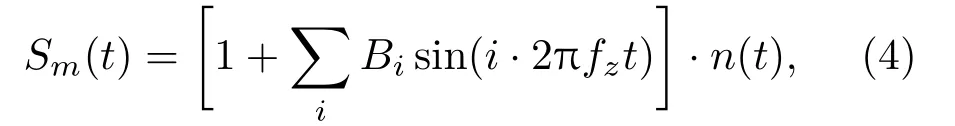
其中，n(t)表示被调制信号，Bi表示调制幅度，fz表示舰艇轴频。由于调制谱来源于螺旋桨空化引发的调制效应，文献[10]中将空化气泡群看成组结构、随机形状与幅度的信号包络模型。在接收点，将N叶螺旋桨空化噪声功率看成各叶片空化声功率的叠加，经过计算包络谱线谱族数学期望值从而得到了信号包络前八阶谐波族特征所体现的结构特性，针对不同螺旋桨叶数研究了不同谐波幅值关系。

对于三叶桨，有

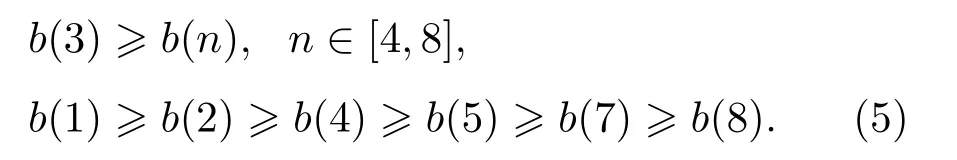
四叶桨：

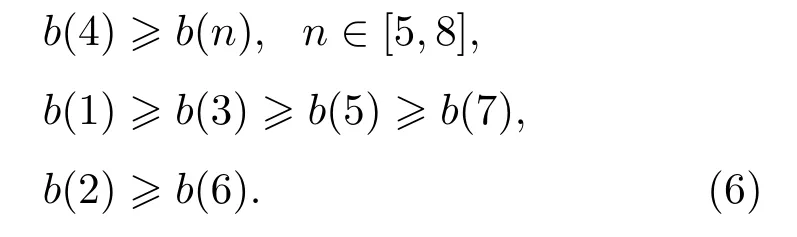
五叶桨：

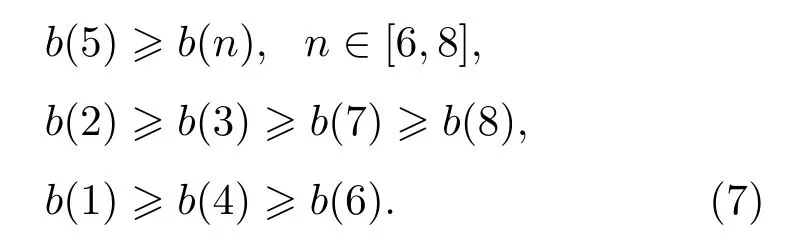
六叶桨：

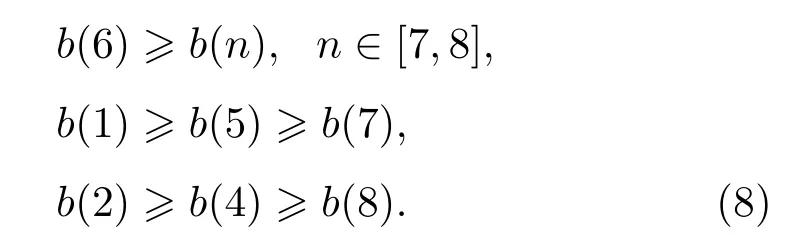
七叶桨：

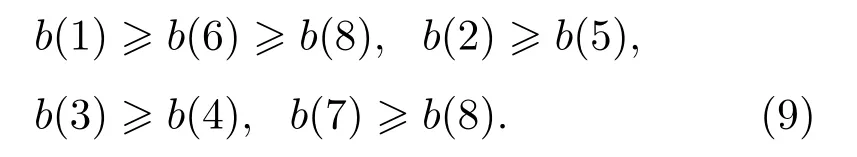
在对大量实测数据进行计算对比的过程中，发现超过75%的样本符合结构特征，说明了在信噪比与平稳性适合的情况下可以用其结构特性来约束调制线谱族的幅值关系，因此本文假设所仿真信号满足结构特征，采用式(5)～式(9)来模拟仿真信号线谱族的大小关系。

4 分频带谱质心计算

以往对于线谱谐波和调制谱谐波族幅度采用随机赋值处理，这样仿真后的信号只能大致模拟其调制信号的节拍频率或者大致反映其特征信息，但是在听音时会感觉到很大差异。在考虑听觉特征时，响度类特征和音调类特征并不能反映人耳主观感知声音的区别，因此人们用音色参量来反映两种相同音调和响度的声音差异[5]。在乐音领域中，谱质心是描述音色属性的重要参量，表征了信号频率的重心，是在一定频带内的加权平均的频率，其计算公式为

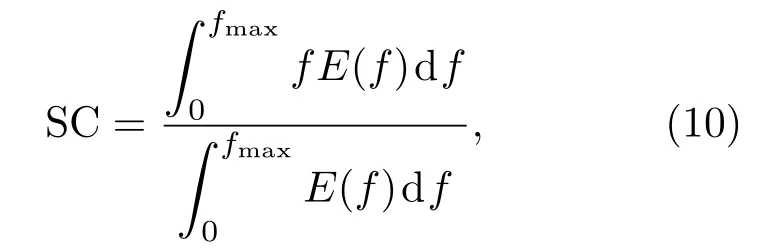
式(10)中，f为信号频率，E(f)表示时域包络x(t)经过短时傅里叶变换后对应频率的谱能量。将式(10)进行适当变换：

式(11)中，E(n)为离散时域信号x(n)短时傅里叶变换后的对应频率的谱能量；N为离散傅里叶变换(Discrete Fourier transformation,DFT)长度；P(E(n))为各部分的能级概率。也就是说谱质心就是每点频率与其对应概率的乘积求和。在识别度上，利用一维谱质心虽然可以在一定程度上反映目标之间的差异，但是随目标种类变化有时会无法区分目标。为了提高不同目标间的区分度，可以将目标频谱划分多个频带进行谱质心分析。对于包络信号，本文采用文献[4]中提出的动态分频法，可以在能量谱集中区域进行多次细分，有效区分目标音色差异，如图4所示。

划分时先在信号全频段计算谱质心，得到SC1，以其为分频点，将频带划分为[0,SC1]和[SC1,fmax]，得到第二层频带。在第二层中分别计算谱质心SC21、SC22，再将其作为分频点，划分第三层频带，以此类推。

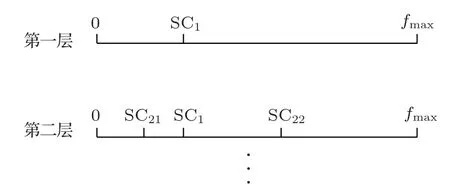
图4 分频带谱质心Fig.4 Mass center of frequency band spectrum

5 特征幅值选取

针对辐射噪声信号，其谱质心影响因素主要来源于线谱幅度，针对特征样本仿真线谱特征幅值，用来代替之前的随机选取，可以改善仿真信号的听觉感受。对于线谱来源，考虑线谱分量的不同组成，将式(2)改写为

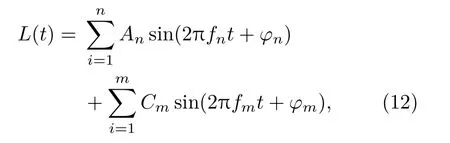
其中，第一部分由受叶片转速影响的速率谱组成，第二部分由机械噪声谱组成，为使仿真过程具有连续性，调制线谱族在式(15)中予以表达。在加入调制谱中的谐波族后，设定归一化特征幅值向量{an,bi,cm}，其中，an、cm、bi分别表示速率谱、机械噪声谱和包络谱线谱族归一化幅度。

将分段谱质心值作为搜索参数，采用最优化理论建立非线性规划模型，寻找在约束条件下与特征样本的最佳匹配方案。设定非线性规划模型：

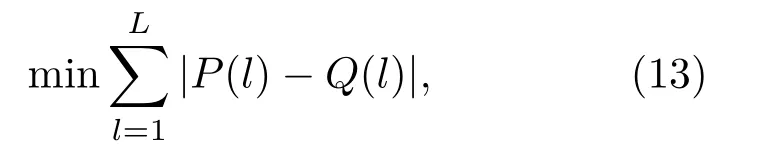
式(13)中，P(l)表示第l层特征样本谱质心值，通过实测数据建立相应类型舰艇辐射噪声音色样本；Q(l)表示划分频带完毕后的仿真信号第l层谱质心值；L表示谱质心频带划分层数，受采样频率和样本点数的制约，具体表示为

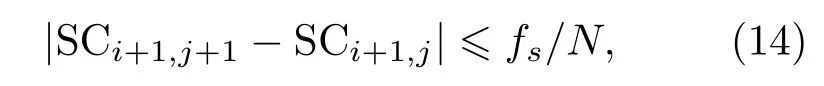
式(14)中，SCi+1,j+1等是频带划分的端点，建立约束条件，规定an,bi,cm ∈(0,1)，且bi满足前文中提出的相应的结构特征。其具体搜索过程为

(1)将采集到的特征样本进行分段谱质心计算，得到{P(l)}。

(2)设定搜索次数N，通过在约束条件下产生N个辐射噪声仿真信号，表示为

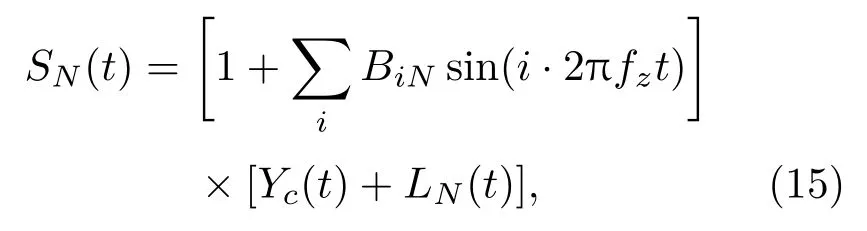
其中，Yc(t)表示按照样本连续谱特征生成的仿真连续谱信号，SN(t)表示单次搜索次数下的仿真信号。

(3)计算仿真信号的分段谱质心QN(l),l=1,···,L。

(4)将仿真值带入模型求解，搜索匹配结果。

(5)在N个匹配结果中提取最小值作为最优匹配结果，当存在多个最优结果时，取频带谱质心方差最小信号输出。

6 算例仿真

通过采集的某四叶桨商船以15 kn 航速匀速航行时的辐射噪声，采样率为5 kHz，进行分段谱质心计算，考虑到计算效率，本文仿真时采用6 段分频，可以在保证区分度的情况下提高计算效率，结果如图5所示。

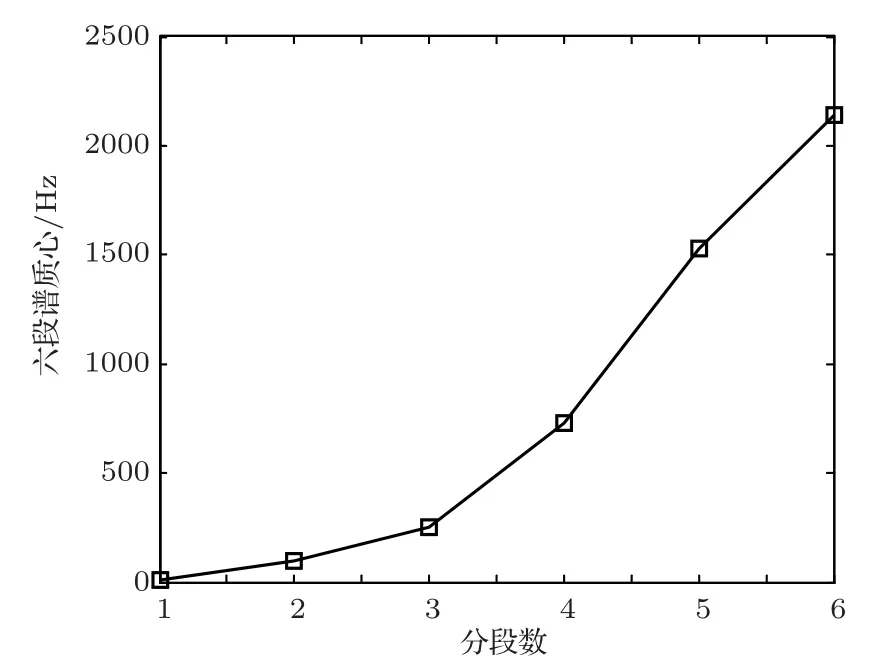
图5 实测样本分段谱质心Fig.5 The measured samples are segmented spectral centroid

按照四叶螺旋桨结构特性与约束条件构建归一化特征幅值向量并组成仿真辐射噪声信号。其轴频在16.7 Hz 附近，叶片速率基频在68 Hz 附近，对于机械噪声，鉴于形成机理的复杂性且主要分布于低频段，按8 条线谱在低频段按谐波取值，最终仿真特征频率点如表1所示。

将表1中的机械噪声线谱频率和螺旋桨噪声线谱频率代入式(12)并设置随机幅值，再将调制线谱频率按照式(5)～式(9)的结构关系设置幅值代入式(15)，仿真得到一系列辐射噪声。计算其各自分段谱质心值，通过固定搜索次数下的数据对比输出最优解，如图6、图7所示。

表1 线谱及调制谱频率Table 1 Line spectrum and modulation spectrum frequency

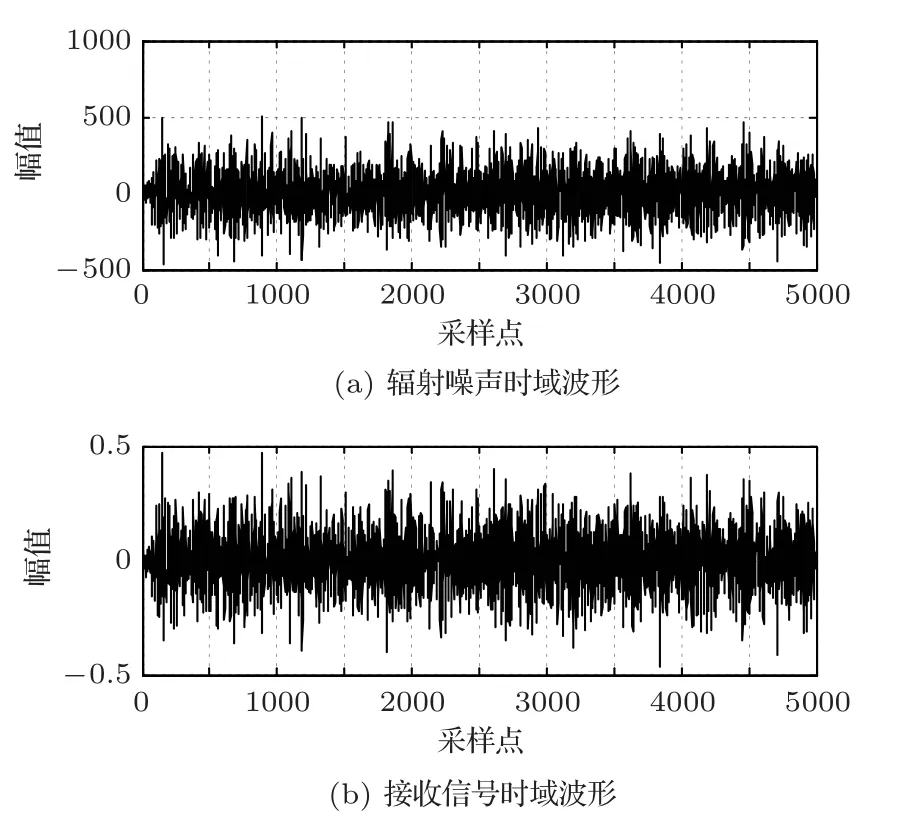
图6 优化输出下仿真时域信号Fig.6 Simulated time domain signal

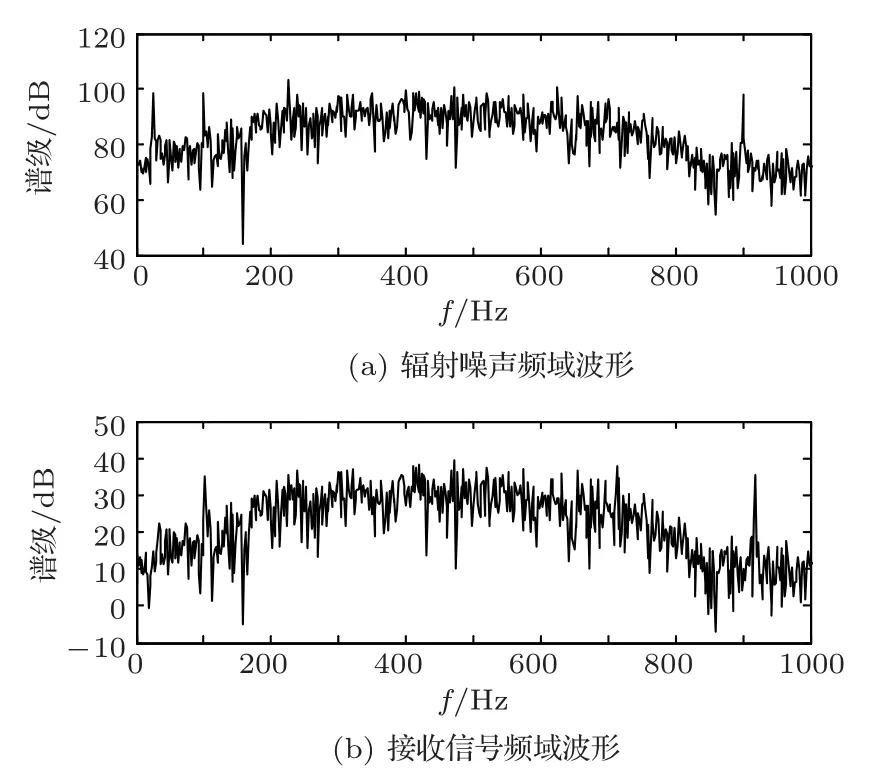
图7 优化输出下仿真频域信号Fig.7 Simulation of frequency domain signals

仿真信号中考虑了目标以15 kn 航速运动产生的多普勒频移以及测量距离在500 m处球面波传播损失后生成了接收端信号。

对比传统方法与基于听觉特征仿真信号的分段谱质心值，如图8所示。可以发现，基于传统随机赋值下的仿真信号在音色参量表达上有一定差距，与实际噪声信号在听觉感官上有较大不同，而基于听觉特性仿真下的信号则具有很好的拟合性。

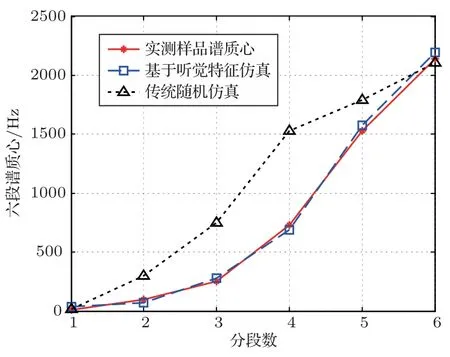
图8 音色参量对比Fig.8 Comparison of timbre parameters

通过声呐员听音识别，实测3 类航船目标在不同航行状态下的辐射噪声，每一类观测10 个样本。针对每一个样本分别采用传统随机仿真与基于听觉特性仿真两种方法生成对比信号，由声呐员判断仿真信号是否达到模拟效果并记录，其识别结果如表2所示。

表2 听音识别结果Table 2 Listening recognition results

由此可以发现，基于听觉特征仿真下的辐射噪声信号从一定程度上改善了仿真信号的听觉特性，可以更好地模拟真实辐射噪声。

为了达到实时性要求，在计算规划模型时需要在保证精度前提下寻找最佳搜索次数，建立最优匹配度α，表示为

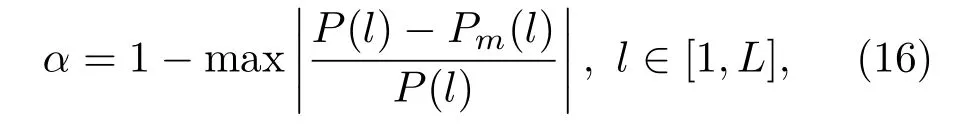
式(16)中，Pm(l)表示在当前搜索次数下的最优匹配结果分段谱质心值。通过仿真不同模型搜索次数结果发现，当N到达一定程度后匹配度随搜索次数的增加变化趋势并不明显，如图9所示。

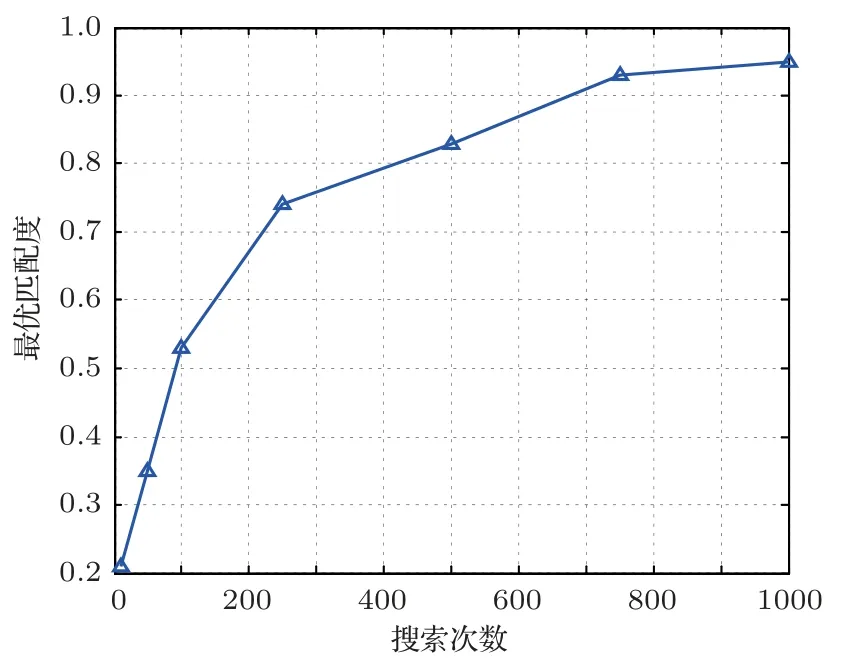
图9 匹配度变化趋势Fig.9 The change trend of matching degree

因此可以设定700为参考搜索次数，可以保证较好的仿真精度下降低计算时间，在搜索后如果结果不理想还可以人为增加。

7 结论

本文通过实测数据构造具有某一类目标听觉特性样本，来调整线谱族特征幅值并由最优匹配度趋势来缩短仿真时间，可以在保证信号特征频谱的前提下改善仿真信号在听觉领域的模拟效果，后续通过叠加不同形式噪声模拟不同传播信道参数，或者改变信噪比等信息生成应用于不同工作的信号，对水声装备发展、信号处理算法检验以及声呐人员训练具有重要意义。当然，谱质心只是描述音色特征的一个参量，通过听音测试可以发现单一谱质心约束不足以模拟全部样本特征，如何通过音色领域的其他参量进行多维度联合仿真是下一步的工作方向。