高中数学正余弦定理在日常生活中的应用
江西省南昌市第十二中学
1 概述
正弦定理和余弦定理搭建了三角形边和角的桥梁,实现了边角之间的转化,直接运用它,可以直接求解三角形,灵活地变形并与其他知识结合,可以解决现实生活中的问题。


2 利用正余弦定理解决平面几何问题

图1 三角形
在解决平面几何问题时,尤其是涉及到三角形,经常会同时利用正余弦定理与其他数学知识,利用正余弦定理解决平面几何问题的题目常常在高考中进行考查。
2.1 判断三角形的形状


结语:判断三角形的形状,本题使用的是余弦定理,我们在解决这类问题的时候,需要观察表达式,正确选择正弦定理或者余弦定理,甚至两者均使用。
2.2 三角形解的个数
对于这个问题,是初学正弦定理的难点,解决这类问题,我们一般采用数形结合的思想,并利用大角对大边的原理来解决,如图2,就是三角形解的四种情况。

图2 三角形解的情况
3 正余弦定理在测量中的应用
3.1 测量距离问题
在解决距离问题时,需要先选取合适的辅助测量点,然后构造出三角形,进而转化成三角形的边角关系,最后利用正余弦定理来解决。测量距离的问题一般分为两点间不可通也不可达、两点间可视但不可通和两点可视但均不可达三种情况。
如图6,是底部可达的情况,可求得高度:


图3
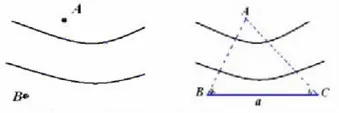
图4
按照解决测量问题的方法,我们可以转化为数学模型,构造出一个三角形,再通过正余弦定理求解。
3.1.3 两点可视但均不可达。最后一种情况是较为复杂的一种,即两点可视但均不可达,如图5所示,仍然假设这是一条小河,则在小河的一边任意选择点C、D,构造出两个三角形。其中可以通过测量仪器测出的数据有:CD=a,∠ADB=α,∠BDC=β,∠ACB=θ,∠ACD=γ。

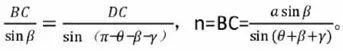
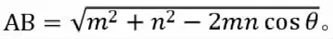
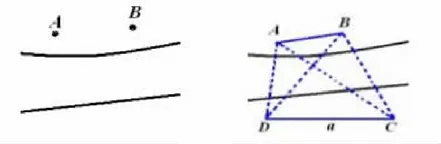
图5
3.2 测量高度问题
对于高度问题一般可以转化为三角形的边角问题,有时候还需要结合几何知识,而对于高度问题,可以分为底部可达和不可达两种情况。

图6


图7
4 正余弦定理的实际应用
在生产和社会生活中,很多地方都会测量距离、高度和角度等数学量,尤其是在物理、航海和工程技术方面,均有解三角形的运用,正确使用正余弦定理就显得十分重要。对于这类题目,本文已经将常见的题型做出了总结,对高考复习也有一定的帮助。

