对一道高三联考试题的解法探究及推广

唐蓓蕾 纪定春

四川师范大学数学科学学院 (610068)

1.问题与评注

(2020年4月名校高三联考文科卷第23题)

已知f(x)=|x|+|x-2|．

评注：该试题结构简单、形式对称、解法丰富、思路开阔，在不等式的证明中具有一定的代表性，特别是问题(2)．由题可知a+2b+2c=2，接下来，主要对问题(2)进行解法探究和推广．

2.解法探究

视角1 判别式法

视角2 向量法

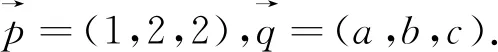
视角3 柯西不等式法

解法3：由柯西不等式得(a+2b+2c)2=(1×a+1×2b+1×2c)2≤(12+22+22)(a2+b2+c2)=9(a2+b2+c2)．即a2+b2+c2≥

视角4 权方和不等式法

视角5 詹森不等式法

视角6 球坐标变换法

解法6：设a2+b2+c2=r2，则有

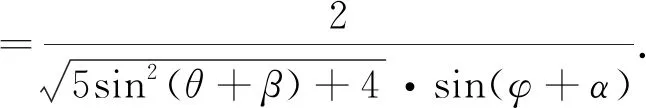
视角7 拉格朗日乘数法

3.问题推广

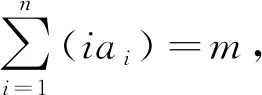
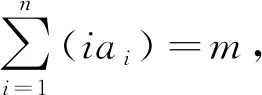
解析：(1)当λ+1<-1或λ+1>0，即λ<-2或λ>-1．