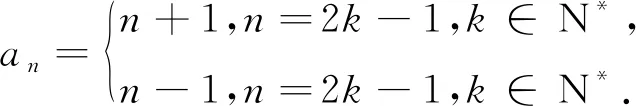一道数列题错解的剖析、修正与再运用

陶炳宏

江苏省海门中学 (226100)

在数学考试中，压轴题一般有一定的难度.学生在有限的时间内对问题的认识与解法有可能存在考虑不全面，认识错误的问题，所以经常出现一些看似正确的错误解法.对于这类错误的解法，教师应该给予深入的分析，帮助学生认识错误的原因，肯定解法中的可取之处，寻找修正的解决办法.下面从一道调研试题学生的错解出发，对解法进行剖析，修正与再运用.

题目(江苏南京盐城2020届高三第二次模拟考试)已知无穷数列{an}的各项均为正整数，其前n项和为Sn，记Tn为数列{an}的前an项和，即Tn=a1+a2+…+aan．

(1)若数列{an}为等比数列，且a1=1，S4=5S2，求T3的值；

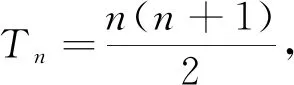
1.错解展示

解：(3)第一步：假设存在n∈N*使得an≤an-1，则Tn=a1+a2+…+aan≤a1+a2+…+aan+aan+1+…+aan-1=Tn-1，这与Tn>Tn-1矛盾，所以∀n∈N*,an>an-1.

2.错在何处

1.第一步表述上存在问题，这一步想要证明数列{an}单调递增，即∀n∈N*,an>an-1.采用反证法证明时，假设的应该为存在某一项不满足an>an-1，这里的n表示的是任意的正整数，而假设的应该是存在某一确定的项，所以应假设存在n0∈N*满足an0≤an0-1更为严谨.反映了学生对于含有全称量词命题的否定掌握的不扎实；

3.解法亮点

虽然解法存在一定的问题，但是存在闪光点.由已知条件可猜想{an}为等差数列，通项公式为an=n.最主要的难点是当ak>k时，前面的k-1项与相应的下标的大小关系如何确定？突破点还是在假设上，应该先找到第一个使得ak≠k的项，这样的话前面k-1项就满足ai=i(1≤i≤k-1)，然后关于的矛盾的说明就合理了.

4.解法修正

解：假设存在n0∈N*使得an0≤an0-1，则Tn0=a1+a2+…+aan≤a1+a2+…+aan+aan+1+…+aan-1=Tn0-1.这与Tn0>Tn0-1矛盾，所以∀n∈N*,an>an-1；因为1=T1=a1+a2+…+aa1≥a1，又a1≥1，所以a1=1.

假设存在an≠n的项，且设满足an≠n的最小正整数为n=k+1,k∈N*，即a1=1,a2=2,…,ak=k,ak+1≠k+1.

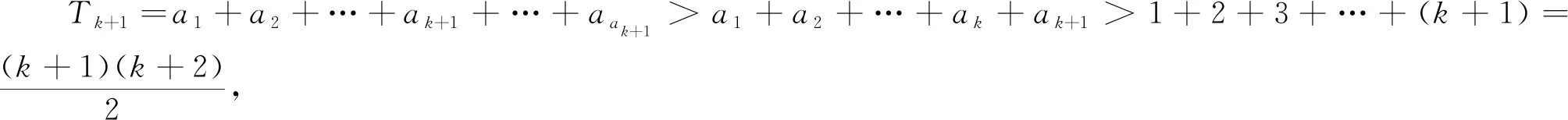
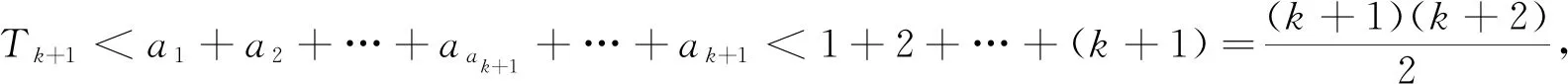
5.方法再运用

上述假设方法在与正整数有关的命题证明中有很多的应用，下面是该方法在2019年上海与北京的高考题中的运用.

例1 (2019上海高考) 数列{an}有100项，a1=a，对任意n∈[2,100]，存在an=ai+d,i∈[1,n-1].若ak与前n项中某一项相等，则称ak具有性质P.

辣椒去籽，粉碎，称取5.0 g，加入40 mL蒸馏水和0.3%(W/W)的纤维素酶，50 ℃反应2 h后进行离心分离，取上清液，残渣用甲醇与四氢呋喃的混合溶液(1∶1，V/V)进行超声提取，温度60 ℃，功率70 W，提取时间1 h，过滤，得到包含辣椒碱和辣椒二氢碱的滤液。

(1)若a1=1，求a4可能的值；

(2)若{an}不为等差数列，求证：{an}中存在满足性质P；

(3)若{an}中恰有三项具有性质P，这三项和为C，使用a,d,c表示a1+a2+…+a100.

分析：第(2)问中数列{an}不为等差数列如何使用，是解决问题的关键点.根据等差数列定义可知{an}中必存在一项满足an≠an-1+d，关键是找出其中的第一个，就可以在找到满足性质P的项.

解：(1)略；(2)证明：因为a2=a1+d，又因为{an}不为等差数列，则存在满足an≠an-1+d(n≥3)的项，设满足an≠an-1+d的项数n的最小正整数为n0，n0≥3，即a2=a1+d,a3=a2+d,…,an0-1=an0-2+1,an0≠an0-1+d.又∀n∈[1,100]，存在an=ai+d,i∈[1,…,n-1]，所以存在i∈[1,…,n0-2]，使得an0=ai+d=ai+1，所以an0具有性质P.(3)略.

例2 (2019北京理)已知数列{an}，从中选取第i1项、第i2项、…、第im项(i1

(1)写出数列1，8，3，7，5，6，9的一个长度为4的递增子列；

(2)已知数列{an}的长度为p的递增子列的末项的最小值为am0，长度为q的递增子列的末项的最小值为an0.若p

(3)设无穷数列{an}的各项均为正整数，且任意两项均不相等.若{an}的长度为s的递增子列末项的最小值为2s-1，且长度为s末项为2s-1的递增子列恰有2s-1个(s=1，2，…)，求数列{an}的通项公式．

分析：第三问的证明思路可分为三步：先证明若偶数是若2m是{an}中的项，则2m必排在2m-1之前，m∈N*.可以采用反证法找到与已知矛盾的地方，第二步证明所有的偶数都是{an}中的项，采用反证法时可以假设不在{an}中的最小的正偶数为2m，从找到与条件“长度为s末项为2s-1的递增子列恰有2s-1个(s=1，2，…)”矛盾的点.

结语试题的错解中隐藏了学生知识的薄弱点、体现了学生的第一想法、展现了学生的思维过程，通过对学生错解的剖析与修正，可以帮助学生厘清知识的盲点、增强学生的自信心、积累数学探究的经验.教师应该重视学生的错解，利用好错解，提高学生的数学素养.