2019年全国Ⅰ卷不等式选做题的探究与启示

谷留明

安徽省合肥市第一中学 (230601)

2011-2018年全国卷一选做题选修4-5考点均为绝对值函数与不等式解集、求值、恒成立问题,而今年突然考查了基本不等式与三个正数的算数-几何平均不等式,值得探究,给教学带来一些启示.

原题呈现

已知为a,b,c正数,且满足abc=1．证明:

(2)(a+b)3+(b+c)3+(c+a)3≥24．

评析:从如何在待证式中出现已知式的结构出发,观察到对左式通分,分母上就会出现abc,将已知条件abc=1正向代入,即发现是证如下结论:bc+ac+ab≤a2+b2+c2.

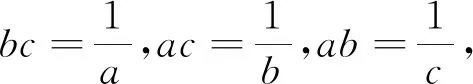
评析：对已知式和待证式观察对比,发现已知式可变形代入,即要证bc+ac+ab≤a2+b2+c2,然后结合重要不等式,用分析法证明.

评析：由待证式联想到常用结论:a2+b2+c2≥bc+ac+ab,并用柯西不等式证明,由已知式abc=1想到“1”的灵活运用，将bc+ac+ab看作分母为1,进行1的逆代.

评析：对左侧三个分子中的1进行逆代.

评析：将待证式左侧看作有系数1,进行逆代.

评析：从右边入手,看作有分母为1,并逆代为a2b2c2,然后同法6,或者直接用结论:a2+b2+c2≥bc+ac+ab的变形形式.

评析：局部代换,出现分子、分母中部分可约.

总评：以上方法看似相近,尤其是法1～5和法6～8,实则思路的出发点、切入点不同,很好的体现出证明不等式的常见经验:左往右、右往左、左右往中间；综合法、分析法、分析综合相结合；1的灵活运用(分母看作1、系数看作1等)；已知条件、公式、常用结论的正用、逆用、变形用；整体、局部代换.另外此问的证明不需要a,b,c为正数,即结论对于满足abc=1的实数a,b,c均成立.

评析：直接运用三个正数的均值不等式,再对三个因式各用基本不等式,很是流畅.此问看似简洁,实则左侧式子与右边结果相隔较远,考生在有限时间内,尤其是考试的靠后阶段不一定能想到流畅的法1思路.

法2:(a+b)3+(b+c)3+(c+a)3≥

评析:与法1相反,先对三个加式各用基本不等式,对结果再用三个正数的均值不等式.

评析:对待证式左侧的三个加式局部展开,局部运用基本不等式进行放缩.再充分利用abc=1,进行局部代换,化为齐次式,重组后再用基本不等式.全程只用到基本不等式,非常巧妙.

评析:法4～6思路相近,都是先将和的立方展开,合理分组,综合使用基本不等式和三个正数的均值不等式.体现出此问证明的灵活性,只要熟练掌握均值不等式,至于怎么、哪里使用,条条大路通罗马,给学生很大的尝试、发挥空间.

题根探源

上述两个问题,均可在人教A版选修4-5习题1.1的三道题中找到踪影.题目如下：

第6题设a,b,c是不全相等的正数,求证:

(1)(a+b)(b+c)(c+a)≥8abc;

第7题求证a2+b2+c2+d2≥ab+bc+cd+da.

其中题6(2)、题7、题11和上述高考题(1)问除abc=1外,本质相同都是在证上文中提到的二级结论,只需分别a,b,c换成a2,b2,c2；a,b,c,d减少为a,b,c；1逆代为(a+b+c)2.高考题(1)问中1的灵活运用,在题11中有很好的体现.题6(1)和高考题(2)问法1中第二步完全一样.

教学启示

2019年考试说明中对不等式选讲中不等式证明的表述是“通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法”.面对纷杂的教辅和试卷,要精选深耕,更要回归课本,课本才是最好的“教辅”.上述高考题,再次表明高考题不神秘,就来源于课本习题.每年高考总要稳重有变,不变的是对学生数学思想与能力、数学六大核心素养的考查验收.教与学都要从题海战术、硬套模型中走出来,真正地以培养能力与素养为目标,方能以不变应万变.