一类带积分边界条件的三阶边值问题正解的存在唯一性

何燕琴，韩晓玲

(西北师范大学数学与统计学院，兰州 730070)

1 引 言

近年来，人们对非线性微分方程可解性的研究非常活跃.这类问题因在流体力学等实际应用中的重要性而备受关注，尤其是二阶和四阶微分方程的研究获得了许多好的结果，但对带积分边界条件的三阶常微分方程边值问题的研究甚少.三阶常微分方程起源于应用数学和物理学的各个不同领域.对其解的存在性已有很多方法，如Guo-Krasnoselskii不动点定理、上下解法，单调迭代法，等[1-11].

2014年，赵亚红等[1]运用Guo-Krasnoselskii不动点定理研究了带积分边界条件的三阶边值问题

的单调正解的存在性，但未讨论正解的唯一性.

2017年，郝彩云等[3]运用混合单调算子不动点定理研究了带积分边界条件的三阶边值问题

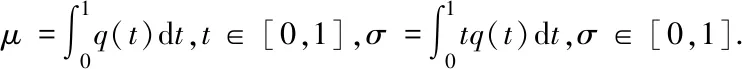
受上述文献启发，本文运用混合单调算子的方法研究了带积分边界条件的三阶边值问题

(1)

单调正解的存在性,其中f:[0,1]×[0,+∞)2→[0,+∞)连续,g:[0,1]×[0,+∞)→[0,+∞)连续.

本文假设下面条件成立：

(H1)f:[0,1]×[0,+∞)2→[0,+∞)连续；

(H2)g:[0,1]×[0,+∞)→[0,+∞)连续；

本文的工作空间是E=C[0,1].定义范数

‖u‖=max{|u(t)|:t∈[0,1]}.

则Ε为实的Banach空间.令Ρ={u∈C[0,1]:u(t)≥0,t∈[0,1]}.则Ρ为Ε中的正规锥.

2 预备知识

设(E,‖·‖)是一个实Banach空间，θ为Ε中的零元素，Ρ⊂E为非空凸闭集.如果P满足：(i)x∈E,λ≥0⟹λx∈Ρ，(ii)x∈Ρ,-x∈Ρ⟹x=θ，则称Ρ为Ε中的一个锥.

设Ρ是Banach空间Ε中的锥，若存在常数N>0,使得对于任意的x,y∈E,当θ≤x≤y时恒有‖x‖≤N‖y‖，则称Ρ是正规的，其中Ν称为Ρ的正规常数.由锥Ρ可诱导Ε中的偏序关系如下：x,y∈Ε,x≤y⟺y-x∈Ρ.对任意的x,y∈Ε,引入等价关系x～y：存在常数μ>0及ν>0，使得μx≤y≤νx.对于给定的h>θ,记集合Ρh为h所在的等价类,即Ρh={x∈Ε|:x～h},Ρh⊂Ε.

定义2.1[2]设D⊆Ε,Α:D×D→Ε是一个算子.如果Α(x,y)关于x是增算子,关于y是减算子,即对任给的y∈D,若x1,x2∈D,x1≤x2,则Α(x1,y)≤Α(x2,y)；对任给x∈D,若y1,y2∈D,y1≥y2，则有Α(x,y1)≤Α(x,y2),则称Α是混合单调算子.

定义2.2[7]若对于任意的t>0,x∈Ε,算子Α:Ε→Ε满足Α(tx)=tΑx,则称A为齐次算子.若对任意的t>0,x∈Ρ,算子Α:Ρ→Ρ满足Α(tx)≥tΑx,则称Α为次齐次算子.若存在一个实数γ，满足0≤γ<1，使得对于任意的t∈[0,1],x∈Ρ，算子Α:Ρ→Ρ满足Α(tx)≥tγΑx，则称Α为凹算子.

定理 2.3[2]设α∈(0,1),h∈Ε,且θ0,使得Α(x,y)≥δ0Βx,∀x,y∈Ρ，则

(i)Α:Ρh×Ρh→Ρh,Β:Ρh→Ρh；

(ii) 存在u0,υ0∈Ρh和r∈(0,1),使得当rυ0≤u0≤υ0时,有u0≤Α(u0,υ0)+Βu0≤Α(υ0,u0)+Βυ0≤υ0；

(iii) 存在唯一的x*∈Ρh,使得x*=Α(x*,x*)+Βx*；

(iv) 以任意的x0,y0∈Ρh为初始元素,定义序列xn=Α(xn-1,yn-1)+Βxn-1,n=1,2,3,…，yn=Α(yn-1,xn-1)+Βyn-1,n=1,2,3,…,满足

引理2.4[5]对任意给定的h∈C[0,1],边值问题

(2)

有唯一解u(t),且u(t)可以表示成下列形式：

其中

引理2.5对于任意给定的(t,s)∈[0,1]×[0,1],G(t,s)有如下性质：

(ii) 当0≤s≤t≤1时,

当0≤s≤t≤1时,

3 主要结果

定理3.1设(H1)～(H3)成立,且

(i) 对固定的t∈[0,1],f(t,x,y)关于x单调递增,关于y单调递减,g(t,x)关于x单调递增；

(ii) 对任意的λ∈(0,1),t∈[0,1],和x∈[0,+∞)有g(t,λx)≥λg(t,x),且存在t0∈[0,1]使得g(t0,0)>0；

(iii) 对任意的λ∈(0,1),t∈[0,1]和x,y∈[0,∞),存在一个常数γ∈(0,1)使得

f(t,λx,λ-1y)≥λγf(t,x,y)；

(iv) 对任意t∈[0,1]和x,y∈[0,+∞),存在一个常数δ0>0,使得f(t,x,y)≥δ0g(t,x)，

则有

(i) 存在u0,υ0∈Ρh,α∈(0,1),使得αυ0≤u0≤υ0,且

其中h(t)=t,t∈[0,1];

(ii) 问题(1)有唯一正解x*∈Ρh(x*(t)>0,t∈(0,1));

(iii) 对任意的x0,y0∈Ρh,以x0,y0为初始元素定义迭代序列

则

证明 由引理2.4,问题(1)的解等价于如下积分方程的解：

定义算子Α:Ρ×Ρ→Ρ为

定义算子

Β:Ρ→Ρ为

其中t∈[0,1],u,υ∈Ρ.当且仅当x=Α(x,x)+Βx时，x为积分方程(1)的解.

接下来我们验证定理2.3的所有条件是否满足.由(i)可知,Α是一个混合单调算子,Β是增函数.由条件(iii),对任意的λ∈(0,1),x,y∈Ρ,有

Α(λx,λ-1y)(t)=

λγΑ(x,y)(t),γ∈(0,1).

这说明算子Α满足定理2.3中的条件.

接下来我们证明Β是一个可齐次算子.对任意的λ∈(0,1),x∈Ρ,考虑(ii)则有

从而Β是一个可齐次算子.

然后我们后来证Α(h,h)∈Ρh,Βh∈Ρh.当h∈Ρ时,定义函数h(t)=t,t∈[0,1].由引理2.5和条件(i)有

另一方面

令

则α1h≤Α(h,h)≤α2h.

接下来我们证明αi>0，i=1,2.实际上,因为g(t0,0)>0,t0∈[0,1]，由f和g的连续性,我们可以找到一个子集Ε⊂[0,1]使得t0∈Ε,μ(Ε)>0,其中μ表示勒贝格度量,g(t,0)>0,t∈Ε.由条件(iv)可得到f(s,0,1)≥δ0g(s,0)≥0.所以

故Α(h,h)∈Ρh.

再由引理2.5和条件(i)有

另一方面,因0≤h(t)≤1，对任意的t∈[0,1]，有

令

则β1h≤Βh≤β2h.为了证明Βh∈Ρh,即βi>0,i=1,2，需证β1>0.又

则Βh∈Ρh.

最后证明定理2.3中的假设条件(i)满足.由u,υ∈Ρ,t∈[0,1]及条件(iv)有

即Α(u,υ)≥δ0Βu.因此,由定理2.3,对任意的t∈[0,1],0

考虑非线性边值问题

从而定理3.1中的条件(iv)是满足的.