关于第二类 Stirling 数的p-adic 赋值的一些新结果

赵 伟，邱 敏

(1.保密通信重点实验室，成都 610041; 2.西华大学理学院，成都 610039)

1 Introduction

Letnandkbe nonnegative integers. The Stirling number of the first kind，denoted bys(n,k)，counts the number of permutations ofnelements withkdisjoint cycles. One can also characterizes(n,k) by

where(x)nis the falling factorial which is defined by

(1)

Note that the exact value of Stirling number of the second kindS(n,k) equals the sum of all products ofn-knot necessarily distinct integers from {1,2，…,k}，i.e.，the following explicit formula holds:

whereNstands for the set of all the nonnegative integers. One can also characterize the Stirling number of the second kind by

and there holds the recurrence relation

S(0,0)=1，S(n,0)=0

and

S(n,k)=kS(n-1,k)+

S(n-1,k-1) ，n≥k≥1.

Furthermore，we have the following two generating functions of Stirling numbers of the second kind:

The Stirling numbers of the first and second kind can be considered to be inverse of one another:

Divisibility properties of Stirling numbers have been studied from a number of different perspectives. Amdeberhan，Manna and Moll[1]studied the 2-adic valuations of Stirling numbers of the second kind，they also conjectured thatv2(S(4n,5))≠v2(S(4n+3,5)) if and only ifn∈{32j+7:j∈N}. Hongetal. proved this conjecture in Ref.[7]. Lengyel[9]conjectured，proved by Wannemacker[12]，a special case of the 2-adic valuation ofS(n,k):v2(S(2n,k))=s2(k)-1，independently ofn，wheres2(k) means the base 2 digital sum ofk. By using Wannemacker’s result，Hongetal.[7]proved that

v2(S(2n+1,k+1))=s2(k)-1

holds for allkwith 1≤k≤2n，which confirmed another conjecture of Amdeberhan，Manna and Moll[1]. We also note that the 2-adic valuation of the Stirling number of the second kind was studied by Zhao，Hong and Zhao in Refs.[13-14].

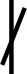
vp(m1m2)=vp(m1)+vp(m2).

Furthermore,for any rational numberxandywe have

vp(x+y)≥min{vp(x),vp(y)},

and ifvp(x)≠vp(y) then one has

vp(x+y)=min{vp(x),vp(y)}.

The above property is also known as the isosceles triangle principle[16].

For every odd primep，we have 2p-1≡1(modp). An odd primepsuch that 2p-1≢1(modp2) is called a Wieferich prime，see Ref.[17]. For example，3，5 and 7 are Wieferich primes. We have the following result，which gives a new method of determining Wieferich prime.

Theorem1.1For any odd primep，we have

vp(S(p,2))≥1,

where the equality holds if and only ifpis a Wieferich prime.

(2)

wheresp(k) andsp(n) stand for the basepdigital sum ofkandn，respectively. Now for the case thatnis a power ofp，we arrive at the following two results，which improve Adelberg’s result in this case，and are the main results of this paper.

Theorem1.2Letnbe an integer withn≥2. For any odd primep，we have

vp(S(pn,2p))≥n.

Theorem1.3Letnbe an integer withn≥2. For any primep≥5，we have

vp(S(pn,4p))≥n-2.

Evidently，forn≥4，the lower bounds ofvp(S(pn,2p)) andvp(S(pn,4p)) in Theorems 1.2 and 1.3 are better than Adelberg’s result (2).

We organize this paper as follows. Firstly，in Section 2 we show some preliminary lemmas which are needed in the proofs of Theorems 1.1 to 1.3. Then in Section 3，we give the proofs of Theorems 1.1 to 1.3.

2 Preliminaries

In this section，we present several auxiliary lemmas that are needed.

Letnandkbe positive integers. By convention，we setS(0,0)=1 andS(n,0)=S(0,k)=0. It is also clear to see thatS(n,k)=0 ifn

S(n,1)=1

and

S(n,2)=2n-1-1，n≥2

(3)

Letmbe a positive integer. The Euler phi functionφ(m) counts the number of integers in the set {1,...,m} that are relatively prime tom. For example，we haveφ(1)=1 andφ(6)=2. Ifpis a prime number，then (a,p)=1 holds for anyawitha∈{1,...,p-1}，and soφ(p)=p-1. Letr≥2 be an integer. Ifpris a prime power，thenφ(pr)=pr-pr-1.

Lemma2.1(Euler) Letmbe a positive integer and letabe an integer relatively prime tom. Then

aφ(m)≡1 (modm).

The following result plays a crucial role in the proofs of Theorem 1.2 and Theorem 1.3.

Lemma2.2Letpbe an odd prime. Letn，k，ibe positive integers such that 1≤k≤p-1，1≤i≤kp-1 and (i,p)=1. We have

vp((kp-i)pn+ipn)=n+1.

ProofLetibe an integer with 1≤i≤kp-1 and (i,p)=1. Sincepis odd，we can deduce that

(4)

For any integerjwith 1≤j≤pn，it follows from (i,p)=1 that

vp(ipn-j)=(pn-j)vp(i)=0

(5)

Since 1≤k≤p-1，one then derives that

vp(kpn+1·ipn-1)=

vp(k)+vp(pn+1)+vp(ipn-1)=n+1

(6)

In what follows，let 2≤j≤pn. Note that

andvp(j′)

(7)

Then it follows from (5) together with 1≤k≤p-1 and (7) that

vp(ipn-j)=n+j-vp(j)

(8)

It is easy to check thatj-vp(j)≥2. In fact，for the case thatvp(j)=0，we havej-vp(j)≥2 sincej≥2，and ifvp(j)≥1，then byp≥3 one deduces thatj≥pvp(j)≥vp(j)+2. Hence by (8) and (6) we derive that

n+j-vp(j)≥n+2>n+1=

vp(kpn+1·ipn-1)

(9)

Using the isosceles triangle principle together with (4)，(6) and (9)，one then arrives at

vp((kp-i)pn+ipn)=vp(kpn+1·ipn-1+

vp(kpn+1·ipn-1)=n+1.

This finishes the proof of Lemma 2.2.

3 The proof of the main results

In this section，we give the proofs of Theorems 1.1 to 1.3. We begin with the proof of Theorem 1.1.

ProofofTheorem1.1For any given odd primep，we have

S(p,2)=2p-1-1.

By Lemma 2.1，one knows that

S(p,2)=2p-1-1≡0 (modp).

It infers thatvp(S(p,2))≥1 with the equality holding if and only if

2p-1-1≢0 (modp2),

i.e.,

2p-1≢1 (modp2),

which is equivalent topbeing a Wieferich prime. So Theorem 1.1 is proved.

Then we present the proof of Theorem 1.2.

ProofofTheorem1.2Letpbe an odd prime. Replacingnbypnandkby 2pin (1)，one gets that

(10)

(11)

Then it follows from (10) and (11) that

(12)

Letibe an integer with 1≤i≤p-1. By settingk=2 in Lemma 2.2 we deduce that

vp((2p-i)pn+ipn)=n+1

(13)

((2p-i)pn+ipn))}}-2=

min{pn,n+2}-2=n.

This completes the proof of Theorem 1.2.

Finally，we give the proof of Theorem 1.3.

ProofofTheorem1.3Letp≥5 be an odd prime. Replacingnbypnandkby 4pin equation (1)，one obtains that

(14)

where

and

(15)

and

(16)

Then it follows from (15) and (16) that

(17)

and

(18)

For any integerisuch that 1≤i≤p-1 orp+1≤i≤2p-1，by using Lemma 2.2 one derives that

vp((4p-i)pn+ipn)=n+1

(19)

Now from (19) together with (17) and (18) we obtain that

n+2

(20)

and

n+2

(21)

(22)

It then follows from (14) together withvp((4p)!)=4 and (20) to (22) that

vp(S(pn,4p))=

vp(Δ1+Δ2+Δ3)-vp((4p)!)≥

min{vp(Δ1),vp(Δ2),vp(Δ3)}-4≥

min{pn,n+2,n+2}-4=n-2.

This complete the proof of Theorem 1.3.